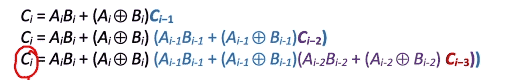BiribiriBird's Gallery.

CUDA编程0基础入门笔记

cuda
字数统计: 2.5k阅读时长: 10 min
2024/05/26
loading

cuda编程 · 零

蒙特卡洛的树 - Cuda编程Bilibili

Github: Cuda_Learning

基本步骤

在进行运行之前，我们可以先查询一下设备中有多少块GPU

1
2
3
int gpuCount = -1;
cudaGetDeviceCount(&gpuCount);
printf("%d ", gpuCount);

然后可以设置成最后一块显卡的ID

cudaGetDevice可以得到当前正在使用的gpu

1
2
3
4
5
6
7
8
9
10
11
int gpuCount = -1;
cudaGetDeviceCount(&gpuCount);
printf("gpuCount = %d\n", gpuCount);

// 1. 指定GPU设别
// 单GPU设备其实可以省略此步骤
cudaSetDevice(gpuCount - 1);

int devideId = -1;
cudaGetDevice(&devideId);
printf("gpu = %d\n", devideId);

当设置不存在的设备编号时，默认启动0号gpu

基本步骤如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <stdio.h>
#include <stdlib.h>
#include <cuda_runtime_api.h>

__global__ void kernel(float *a) {
    a[threadIdx.x] = 1;
}

int main(int argc, char ** argv) {

    int gpuCount = -1;
    cudaGetDeviceCount(&gpuCount);
    printf("gpuCount = %d\n", gpuCount);

    // 1. 指定GPU设别
    // 单GPU设备其实可以省略此步骤
    cudaSetDevice(gpuCount - 1);

    int devideId = -1;
    cudaGetDevice(&devideId);
    printf("gpu = %d\n", devideId);

    // 2. 分配显存空间
    float *aGPU;
    // cudaError_t cudaMalloc(void **devPtr, size_t size);
    // void **devPtr 指向待分配内存空间指针的指针 
    // 		指针是通用的设备指针，可以指向任何类型的内存
    // size_t size 分配的内存大小
    cudaMalloc((void**)&aGPU, 16 * sizeof(float));

    // 3. 分配内存空间
    float a[16] = {0};

    // 4. 内存->显存
    // cudaError_t cudaMemcpy(void* dst, const void* src, size_t count, cudaMemcpyKind kind)
    // 目的地址, 源地址，需要复制的字节数量， 复制类型
        //  cudaMemcpyHostToHost：从主机到主机的内存复制。
        //  cudaMemcpyHostToDevice：从主机到设备的内存复制。
        //  cudaMemcpyDeviceToHost：从设备到主机的内存复制。
        //  cudaMemcpyDeviceToDevice：从设备到设备的内存复制。

    cudaMemcpy(aGPU, a, 16 * sizeof(float), cudaMemcpyHostToDevice);

    // 5. 设备代码
    kernel<<<1, 16>>>(aGPU);
    
    // 6. 显存->内存
    cudaMemcpy(a, aGPU, 16 * sizeof(float), cudaMemcpyDeviceToHost);

    for (int i=0;i<16;++i)
        printf("%.2lf ", a[i]);

    // 7. 释放
    cudaFree(aGPU); // 释放申请的显存
    cudaDeviceReset(); // 重置设备
    // 如果主机内存也有申请 也需要释放
}

GPU详细信息

cudaDeviceProp是cuda封装的一个显卡信息结构体

我们可以通过这个结构体查看显卡信息

1
2
3
4
5
6
7
8
9
10
11
cudaDeviceProp prop;
// 指定0号显卡
cudaGetDeviceProperties(&prop, 0);

printf("maxThreadsPerBLOCK: %d\n", prop.maxThreadsPerBlock);
printf("maxThreadsDim: %d\n", prop.maxThreadsDim[0]);
printf("maxGridSize: %d\n", prop.maxGridSize[0]);
printf("totalConstMem: %d\n", prop.totalConstMem);
printf("clockRate: %d\n", prop.clockRate);
printf("integrated: %d\n", prop.integrated);

还有一些别的东西

1
2
3
4
5
6
7
// 程序可以在多个 CUDA 设备上运行时，可以使用这个函数来选择一个最合适的设备 device会变成被选中的设备编号 
// prop需要填写需求 自动匹配符合要求的设备
cudaError_t cudaChooseDevice(int* device, const cudaDeviceProp* prop)

// 传入一个编号数组和数组长度
// 只有编号在其中的设备会是有效设备
cudaError_t cudaSetValidDevices(int *device_arr, int len);

Cuda项目建立

建立项目文件夹，新建CMakeLists.txt

1
2
3
4
5
cmake_minimum_required(VERSION 3.22)
project(app LANGUAGES CUDA CXX)
find_package(CUDA REQUIRED)
CUDA_ADD_EXECUTABLE(app main.cu)
TARGET_LINK_LIBRARIES(app)

在同文件夹下建立一个main.cu

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <stdio.h>
#include <stdlib.h>
#include <cuda_runtime_api.h>

__global__ void add(int *a, int *b, int *c, int num) {
	if ( threadIdx.x < num ) 
		c[threadIdx.x] = a[threadIdx.x] + b[threadIdx.x];
}

int main(int argc, char ** argv) {
	
	int num = 10;
	int a[num], b[num], c[num];
	
	for (int i=0;i<num;++i) a[i] = i;
	for (int i=0;i<num;++i) b[i] = i * i;

	int *agpu, *bgpu, *cgpu;
	
	cudaMalloc((void**)&agpu, num * sizeof(int));
	cudaMalloc((void**)&bgpu, num * sizeof(int));
	cudaMalloc((void**)&cgpu, num * sizeof(int));

	cudaMemcpy(agpu, a, num * sizeof(int), cudaMemcpyHostToDevice);
	cudaMemcpy(bgpu, b, num * sizeof(int), cudaMemcpyHostToDevice);

	// 加法
	add<<<1, 10>>>(agpu, bgpu, cgpu, num);
	cudaMemcpy(c, cgpu, num * sizeof(int), cudaMemcpyDeviceToHost);
	
	printf("add:\n");
	for (int i=0;i<num;++i) printf("%d + %d = %d\n", a[i], b[i], c[i]);

	cudaFree(agpu); 
	cudaFree(bgpu); 
	cudaFree(cgpu); 
    cudaDeviceReset(); 
}

新建build文件夹

1
2
3
4
mkdir buid && cd build
cmake ..
make -j3
./app

手写卷积

什么是卷积？【官方双语】那么……什么是卷积？

首先需要添加一个新的东西：CUDA_CHECK

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#define CUDA_CHECK(call) \
do { \
    cudaError_t err = call; \
    if (err != cudaSuccess) { \
        fprintf(stderr, "CUDA error at %s:%d code=%d(%s) \"%s\"\n", \
                __FILE__, __LINE__, err, cudaGetErrorString(err), #call); \
        exit(EXIT_FAILURE); \
    } \
} while (0)

// 后续我们使用Cuda函数时 用宏进行包装
// 即可及时报错
CUDA_CHECK(cudaMalloc(&devPtr, size));

code见code/src/code_2.cu

并行归约Parallel Reduction

我们需要对一个数组进行并行算法的求和

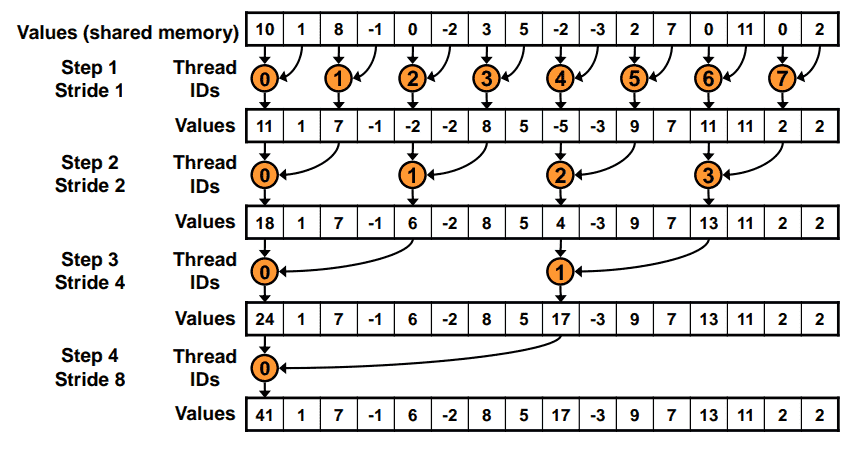
交错寻址

image-20240402123917253

两两求和，逐渐合并

但是这样寻址速度较慢

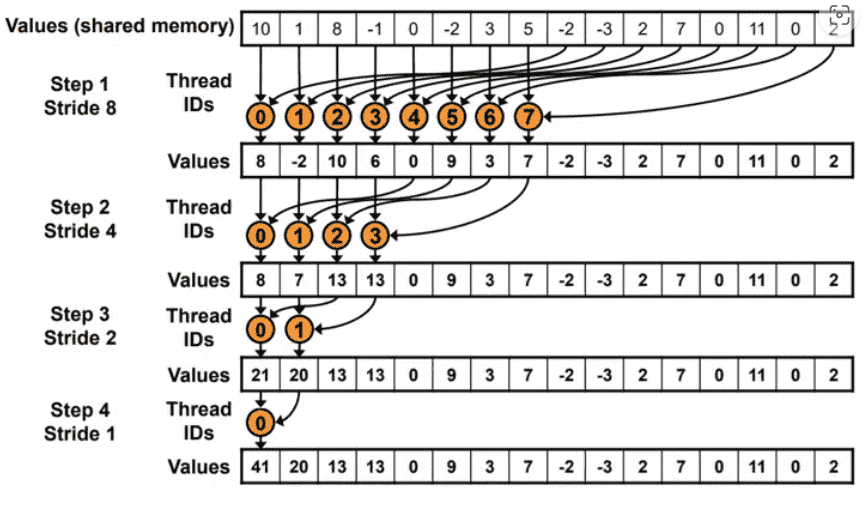
连续地址

image-20240402124057146

code见code/src/code_3.cu

程序计时

推荐使用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <sys/time.h>

	struct timeval startTime, endTime;
	
	// 获取开始时间
    gettimeofday(&startTime, NULL);

    // 执行一些操作

    // 获取结束时间
    gettimeofday(&endTime, NULL);

    // 计算时间差
    long long elapsedTime = (endTime.tv_sec - startTime.tv_sec) * 1000000LL + (endTime.tv_usec - startTime.tv_usec);

    printf("Elapsed time: %lld microseconds\n", elapsedTime);

其中，sys/time.h 是一个 C 标准库头文件，通常用于在 POSIX 操作系统中进行时间操作，因此在 POSIX 兼容的操作系统上使用时通常是可用的，比如 Linux 和 macOS 等。

这里我们对手写卷积进行了测速

code见code/src/code_4.cu

并且我们发现，我们一个block一次计算，和一个thread一次计算

效率基本一致

并且放在thread可以共享内存，所以推荐放在thread里

原子操作

原子操作是一种不可分割的操作，它要么完全执行，要么完全不执行，没有中间状态。

在并发编程中，原子操作是一种确保多个线程或进程安全访问共享资源的机制。

原子操作能够保证在多线程环境下不会出现数据竞争的情况，从而确保数据的一致性和正确性。

原子操作的特性包括：

  1. 不可分割性：原子操作是一个不可分割的操作，它要么完全执行，要么完全不执行，不会被中断或分割成更小的部分。
  2. 独占性：在原子操作执行期间，其他线程或进程无法访问被操作的资源，直到原子操作执行完成。
  3. 并发安全性：多个线程或进程可以同时执行原子操作，而不会导致数据竞争或数据不一致的情况。

银行转账，当钱被转出时若发生中断，则此时钱就少了

因此转出和转入必须完整执行完毕

实例

统计每种数字出现多少次

如果在核函数中

1
hist[ a[id] ] ++;

由于会有多个核函数并行操作，每次hist的值都不一致

会造成值操作的覆盖

因此引入了atomicAdd()，自动为数据上锁，在完成一次加法之间，不允许被其他thread使用

code见code/src/code_5.cu

共享内存

使用__shared__进行声明

同属于一个block的thread共享一个共享内存

静态申请

如果我们一开始就确定要开多少共享内存数组

1
2
__shared__ int s[64];
__shared__ int s[N]; // N is constexpr

动态申请

在核函数指定第三个执行配置参数，数值为需要申请的每个块动态共享内存大小

1
dynamicReverse<<<1, n, n*sizeof(int)>>>();

在核函数内

1
extern __shared__ int s[]; // 此时s即为大小为指定值的数组

如果需要申请多个共享内存数组

1
Kernel<<<g, b, nI*sizeof(int)+nF*sizeof(float)+nC*sizeof(char)>>>();

申请的数值即为所有数组大小之和

1
2
3
4
extern __shared__ int s[];
int *integerData = s;                        // nI ints
float *floatData = (float*)&integerData[nI]; // nF floats
char *charData = (char*)&floatData[nF];      // nC chars

手动切割数组即可

框架thrust

cuda版本的STL

官方地址：https://github.com/NVIDIA/thrust

记录几个比较简单的例子

1
2
3
4
5
6
7
8
9
10
#include <thrust/host_vector.h>
#include <thrust/device_vector.h>

	// 在主机内存中申请 大小为10的vector
	thrust::host_vector<int > a(10);

	for (auto & e : a) std::cin >> e;
	for (auto & e : a) std::cout << e <<" ";

	// 基本和std::vector没什么差别

实例：估算圆周率

code见code/src/code_6.cu

多个block的归约

例如我们要进行一个数组求和，但是数组元素个数远远多于线程

一个block的线程数量有限，一般是1024（看具体设备）

因此我们需要让多个block进行归约

（估算圆周率的实例中，我们使用了1个block进行归约）

  • 把数据切分为若干段，每段数量为总线程数
  • 第一次先把所有数据读到前总线程数个数字内
  • 再细分成block num段，每段thread_num个
  • 分别归约，得到blockNum个数字
  • 数量不会很多的情况下直接CPU计算，节省硬件传输

code见code/src/code_7.cu

多维矩阵

1
2
3
4
5
6
7
8
9
10
11

	size_t width = 120, height = 10;
    float * a_gpu; size_t pitch;

    cudaMallocPitch((void**)&a_gpu, &pitch, width*sizeof(float), height );

    printf("real = %zu\npitch = %zu", width*sizeof(float), pitch);
    cudaFree(a_gpu);

// 当width*sizeof(float)<=512时 pitch=512
// 超过512 pitch取最小的512的倍数

内存对齐，使得访问效率更高

但是我们一行该放多少放多少，剩下的空间直接忽略

暂时先不研究这个，感觉用处不大

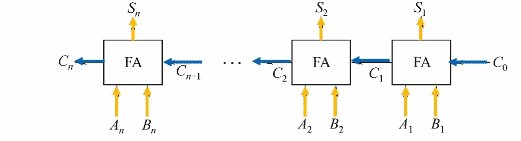
实例：手写全加器

对于串行加法器

image-20240405022231427

高位计算需要等待低位的进位

令Ai+BiA_i+B_i的进位结果为CiC_i，计算结果为SiS_i

则$C_i = 1 $的情况有：

  • Ai=1,Bi=1A_i = 1, B_i = 1同时为1
  • Ai⊗Bi=1,Ci−1=1A_i \otimes B_i = 1, C_{i-1} = 1只有一个1，存在进位1

因此Ci=AiBi+(Ai⊗Bi)Ci−1C_i = A_iB_i + (A_i\otimes B_i)C_{i - 1}

++表示或，⋅\cdot表示并

image-20240405023017938

因此我们可以进行多次展开，每次的进位都可以由C0C_0直接确定

一般来说我们每四位进行并行，然后总体串行即可

code见code/src/code_8.cu

原文作者：BiribiriBird

原文链接：https://aoijays.top/2024/05/26/cuda-zero-2024-5/

发表日期：May 26th 2024, 5:18:35 pm

更新日期：July 28th 2024, 3:53:00 pm

版权声明：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. cuda编程 · 零
    1. 1.1. 基本步骤
      1. 1.1.0.1. GPU详细信息
  2. 1.2. Cuda项目建立
  3. 1.3. 手写卷积
  4. 1.4. 并行归约Parallel Reduction
    1. 1.4.1. 交错寻址
    2. 1.4.2. 连续地址
  5. 1.5. 程序计时
  6. 1.6. 原子操作
    1. 1.6.1. 实例
  7. 1.7. 共享内存
    1. 1.7.1. 静态申请
    2. 1.7.2. 动态申请
  8. 1.8. 框架thrust
  9. 1.9. 实例：估算圆周率
  10. 1.10. 多个block的归约
  11. 1.11. 多维矩阵
  12. 1.12. 实例：手写全加器
Total : 24
2024
CV 动手学深度学习 深度学习 李宏毅 cuda langchain Pytorch 论文笔记 毕业设计