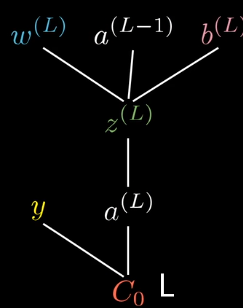手推神经网络
Bilibili
配套资源
神经网络与深度学习
神经网络基础
对于结构化的训练数据,我们记列向量x(i)所构成的矩阵为X
所有label值构成一个行向量Y=[y(1)y(2)...y(m)]
激活函数
对于神经元来说,总是需要一个激活函数的
每个神经元将所有输入进行线性组合后,需要喂入激活函数,输出一个值
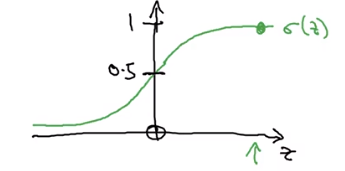
sigmoid函数:
σ(z)=1+e−z1
求导y=σ(z):
y=1+e−z1y′=(1+e−z)2e−z=1+e−x1+e−x−1×1+e−x1=(1−y)y
基本已经不用sigmoid激活函数了,tanh函数在所有场合都优于sigmoid函数
除了二分类问题:需要输出0-1的概率值
tanh可以认为是sigmoid的平移伸缩版本
tanh(z)=ez+e−zez−e−z
求导:
dzdtanh(z)=(ez+e−z)2(ez+e−z)(ez+e−z)−(ez−e−z)(ez−e−z)=1−(ez+e−z)2(ez−e−z)2=1−tanh2(z)
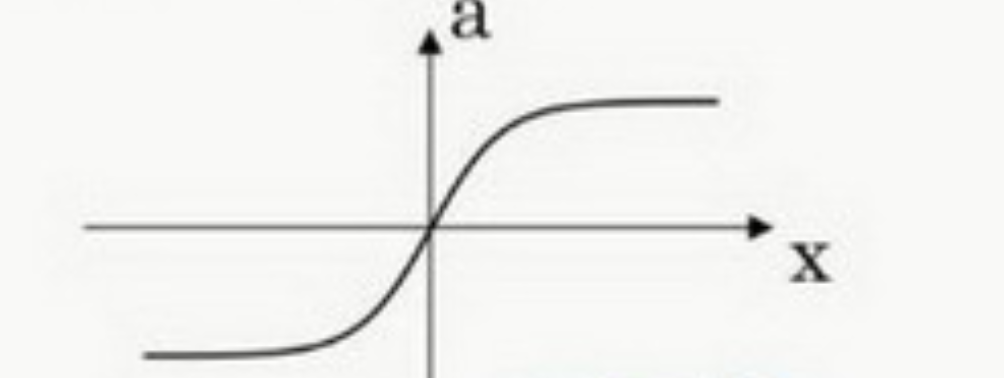
Relu(z)=max(0,z)
在0处导数不存在,但是全部取0的概率非常低
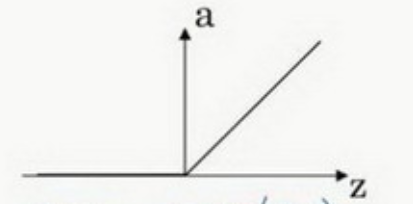
Relu(x)=max(0.01x,x)
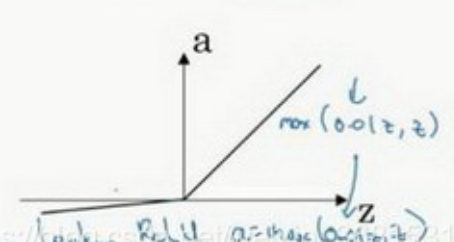
一般推荐使用Relu即可,训练速度快于前两者
sigmoid和tanh函数的导数在正负饱和区的梯度都会接近于0,这会造成梯度弥散
Relu进入负半区的时候,梯度为0,神经元此时不会训练,产生所谓的稀疏性,而Leaky ReLu不会有这问题
但有足够的隐藏层使得z值大于0,所以对大多数的训练数据来说学习过程仍然可以很快
- 梯度弥散:反向传播中,导数连乘,若梯度很小(小于1),就会使得越远离输出层的梯度越小,越靠近输出层的梯度越大。靠近输入层的梯度趋近于0,基本不训练,无法学习输入层特征
- 梯度爆炸:导数很大,数值溢出
激活函数的意义
我们令激活函数g(x)=x,相当于什么都不用做
经过第一层神经网络:a[1]=W[1]x+b[1]
经过第二层神经网络:a[2]=W[2]a[1]+b[2]
我们展开即得:
a[2]=W[2]W[1]x+(W[2]b[1]+b[2])=Wx+b
因此无论网络多么复杂,最后得到的结果都是x的线性组合
- 输出层可以使用g(x)=x线性激活函数(预测房价的结果)
梯度下降
懂的都懂
w:=w−α∂w∂J(w,b)b:=b−α∂b∂J(w,b)
计算图
令J(a,b,c)=3(a+bc)
我们将此成本函数进行分解,引入中间变量
u=bcv=a+uJ=3v
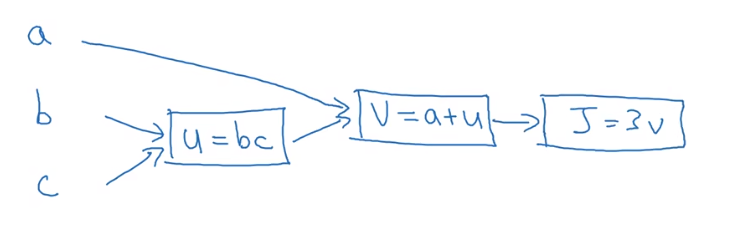
- ∂v∂J=3
- ∂a∂J=∂v∂J×∂a∂v=3×1=3
- ∂u∂J=∂v∂J×∂u∂v=3×1=3
- ∂b∂J=∂u∂J×∂b∂u=3c
- ∂c∂J=∂u∂J×∂c∂u=3b
通过构建计算图,我们从右往左,可以非常容易计算出导数
每个矩形框使用的运算类型,其所代表的求导公式可以提前保存
初始化
若我们初始化所有参数全部为0
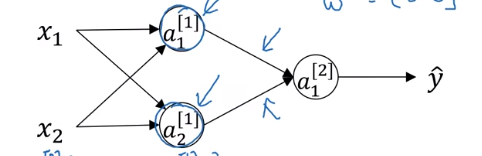
如图,在正向推理时,两个神经元的值完全一致,梯度也完全一致
那么两个神经元并不会有本质差别,后续也会进行一样的计算
因此会产生对称性的效果,多个隐藏层、神经元不会起到效果
因此我们需要随机初始化所有参数
不能过大,否则使用激活函数时会直接爆炸
Logistic Regression
给定X,需要计算出y^=P(y=1∣x)
即符合某种分类的概率
- 输入:X
- 参数:w∈Rn,b∈R
- 输出:y^=σ(wTx+b)
Loss Function损失函数
L(y^,y)=−(ylogy^+(1−y)log(1−y^))
Loss Function是对单个样本的计算
为什么选择上述函数作为损失函数?
我们希望我们的模型输出y^:标签y=1的概率
因此,标签y=0的概率即为:1−y^
即为:
P(y=1∣x)=y^P(y=0∣x)=1−y^
当y=1时,我们期待y^尽可能大,接近1
当y=0时,我们期待1−y^尽可能大,接近1
我们希望统一这两个式子:
P(y∣x)=y^y×(1−y^)1−y
不符合的地方自动会变成1,不影响到结果
因此目标为:最大化这个函数
但这个函数比较抽象,不方便研究
我们知道对数函数是一个单调递增的函数,因此我们对原式同时进行对数操作
logP(y∣x)=log(y^y×(1−y^)1−y)=ylogy^+(1−y)log(1−y^)
我们希望最大化P(y∣x),那么根据单调函数的性质,最大化logP(y∣x)即可
我们需要最大化左边的值,就需要最大化右边
我们加个负号
L(y^,y)=−(ylogy^+(1−y)log(1−y^))
右边的表达式就是损失函数的负值
我们最小化损失函数,与最大化概率值的目的一致
因此作为损失函数非常不错
Cost Function成本函数
J(w,b)=m1∑L(y^(i),y(i))
针对总体成本的函数
神经网络训练目标即为:找到最佳的参数,使得成本函数最小
为什么选择这个作为成本函数?
直觉上是这样
我们考虑从最大似然估计的角度出发
在参数w,b下,所有单个样本等于某个随机值yi的概率就是:∏P(yi∣x)
构造似然函数:L(w,b∣y,x)=∏P(yi∣x)
是一个关于w,b的函数,y,x均为定值
同样,我们希望两边求对数
logL=−∑L(y^,y)
我们令成本函数:
J(w,b)=−m1∑L(y^,y)
乘上一个m1常数因子没什么影响,更加方便
最小化成本函数,即为最大化似然函数,则就是找到了最佳参数组合,使得样本和标签值已知的情况下,概率最大
Logistics Regression的梯度下降
首先考虑单个样本
z(i)=wTx(i)+by^(i)=σ(z(i))L=−(y(i)logy^(i)+(1−y(i))log(1−y^(i)))
我们求出梯度,通常在编程中,我们喜欢使用da表示目标函数关于a的梯度
dy^(i)=∂y^(i)∂L=−y^(i)y(i)+1−y^(i)1−y(i)dz(i)=dy^(i)×∂z(i)∂y^(i)=dy^(i)×(1−y^(i))y^(i)=y^(i)−y(i)
w我们暂时先不看作是一个矩阵向量
我们分别对w1,w2,...即wj进行求导
dwj(i)=dz(i)×∂wj∂z(i)=xj(i)dz(i)=xj(i)(y^(i)−y(i))db(i)=dz(i)×∂b∂z(i)=dz(i)=y^(i)−y(i)
现在我们考虑多个样本,即需要考虑的是成本函数J
事实上:J=m1L(y^(i),y(i))
每个样本之间都是不相干的,我们一个枚举,把所有单个样本的结果:dw,db全部计算出来求和,最后除以m求平均即可

但是对于深度学习问题,我们枚举计算非常低效
解决方法有:
Logistics Regression的梯度下降(向量化版本)
避免显示的for循环
不管是CPU还是GPU,我们都更加推荐使用支持SIMD的函数
充分并行化操作,加快执行效率
- v=[v1,...,vn]T
- ev=[ev1,...,evn]T
大部分函数操作,如abs,log等,都是会自动扩展成矩阵向量形式的
我们首先计算z(i),非向量版本就需要一个个枚举
z(i)=wTx(i)+b
我们可以放在一个矩阵中
z=[z(1)z(2)...z(m)]=[wTx(1)+bwTx(2)+b...wTx(m)+b]=wTX+b
则有:
y^=[y^(1)y^(2)...y^(m)]=[σ(z(1))σ(z(2))...σ(z(m))]=σ[z(1)z(2)...z(m)]=σ(z)
接下来我们计算梯度
dz=[dz(1)dz(2)...dz(m)]=[y^(1)−y(1)y^(2)−y(2)...y^(m)−y(m)]=y^−Y
这也就解释了为什么Y是行向量
列向量表示同一个样本的不同属性
行向量表示多个不同样本
dw=⎣⎢⎢⎢⎡dw1dw2...dwn⎦⎥⎥⎥⎤=m1⎣⎢⎢⎢⎢⎡∑x1(i)dz(i)∑x2(i)dz(i)...∑xn(i)dz(i)⎦⎥⎥⎥⎥⎤=m1⎣⎢⎢⎢⎡x1dzTx2dzT...xndzT⎦⎥⎥⎥⎤=m1XdzT
得到的是一个(n×m)∗(m×1)=(n×1)的矩阵
db=m1∑dz(i)
是一个标量
最后,梯度下降即可以表示为:
w:=w−αdwb:=b−αdb
神经网络
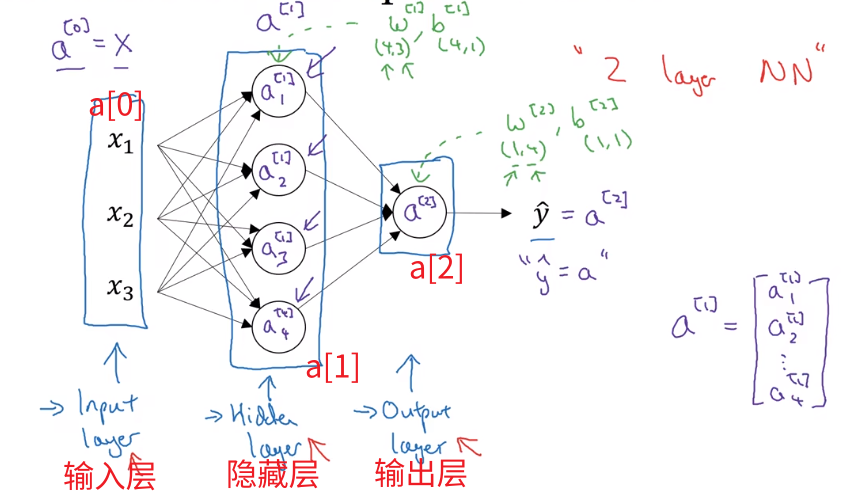
- 一般忽略输入层,称为双层神经网络
- 这里我们使用中括号表示层编号
正向传播:单个样本的计算
我们有一个需要计算的样本x,现在需要通过神经网络计算其y^
以上述双层神经网络为例,第一层的结果为:
a[1]=⎣⎢⎢⎢⎢⎡a1[1]a2[1]a3[1]a4[1]⎦⎥⎥⎥⎥⎤=σ⎣⎢⎢⎢⎢⎡w1[1]Tx+b1[1]w2[1]Tx+b2[1]w3[1]Tx+b3[1]w4[1]Tx+b4[1]⎦⎥⎥⎥⎥⎤=σ(⎣⎢⎢⎢⎢⎡...w1[1]......w2[1]......w3[1]......w4[1]...⎦⎥⎥⎥⎥⎤⎣⎢⎡x1x2x3⎦⎥⎤+⎣⎢⎢⎢⎢⎡b1[1]b2[1]b3[1]b4[1]⎦⎥⎥⎥⎥⎤)
需要注意,wj[i]是每个神经元的参数向量,之前的表示是一个列向量
这里我们把它变成行向量,构成矩阵W[1]的一个行向量
则有:
a[1]=σ(W[1]x+b[1])
对于第二层也是同理进行计算即可
a[2]=σ(W[2]a[1]+b[2])
正向传播:多个样本的计算
我们最终需要得到矩阵A
首先计算第一层神经网络的结果:
A[1]=[a[1](1)a[1](2)...a[1](m)]
每个列向量a[1](i)表示第i个样本经过第一层神经网络计算得到的结果
A[1]=σ[W[1]x(1)+b[1]W[1]x(2)+b[1]...W[1]x(m)+b[1]]=σ(W[1][x(1)x(2)...x(m)]+b[1])=σ(W[1]X+b[1])
第二层同理:
A[2]=σ(W[1]A[1]+b[1])
反向传播:单个样本的计算
需要明白,梯度矩阵和原矩阵的形状不变
我们使用损失函数:
L(w,b)=21(y^(i)−y(i))2
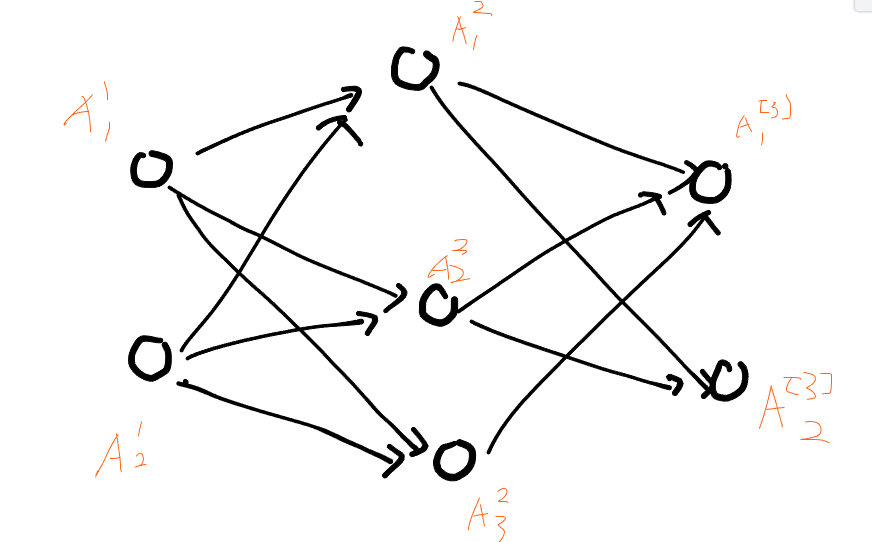
我们对如上神经网络进行反向传播
先看一下计算图
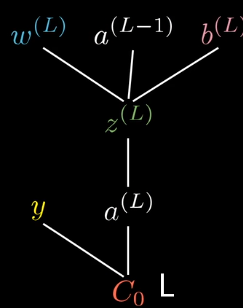
符合略微不同,但是问题不大
以下式子中,我们省略样本编号(i)
例如:A[3]=[A1[3]A2[3]],表示了单个样本的输出
-
输出层
-
dA[3]=∂A[3]∂L=[A1[3]−y1A2[3]−y2]
-
dZ[3]=∂Z[3]∂L=∂A[3]∂L∂Z[3]∂A[3]=[(A1[3]−y1)σ′(Z1[3])(A2[3]−y2)σ′(Z2[3]))]
-
db[3]=∂Z[3]∂L∂b[3]∂Z[3]=[(A1[3]−y1)σ′(Z1[3])(A2[3]−y2)σ′(Z2[3]))]=dZ[3]
-
dw[3]=∂Z[3]∂L∂w[3]∂Z[3]=[(A1[3]−y1)σ′(Z1[3])A1[2](A2[3]−y2)σ′(Z2[3])A1[2]......(A1[3]−y1)σ′(Z1[3])A3[2](A2[3]−y2)σ′(Z2[3])A3[2]]=[(A1[3]−y1)σ′(Z1[3])(A2[3]−y2)σ′(Z2[3]))][A1[2]A2[2]A3[2]]=dZ[3]A[2]T
-
隐藏层2
-
dA[2]=∂Z[3]∂L∂A[2]∂Z[3]=⎣⎢⎢⎡dZ1[3]w1,1[3]+dZ2[3]w2,1[3]dZ1[3]w1,2[3]+dZ2[3]w2,2[3]dZ1[3]w1,3[3]+dZ2[3]w2,3[3]⎦⎥⎥⎤=⎣⎢⎢⎡w1,1[3]w1,2[3]w1,3[3]w2,1[3]w2,2[3]w2,3[3]⎦⎥⎥⎤[(A1[3]−y1)σ′(Z1[3])(A2[3]−y2)σ′(Z2[3]))]=w[3]TdZ[3]
-
dZ[2]=⎣⎢⎢⎡dA1[2]σ′(Z1[2])dA2[2]σ′(Z2[2])dA3[2]σ′(Z3[2])⎦⎥⎥⎤
-
db[2]=⎣⎢⎢⎡dA1[2]σ′(Z1[2])dA2[2]σ′(Z2[2])dA3[2]σ′(Z3[2])⎦⎥⎥⎤=dZ[2]
-
dw[2]=dZ[2]A[1]T
-
隐藏层1(我们假装前面还有一个输入层A0没画出来,多推几层看看规律)
-
dA[1]=w[2]TdZ[2]
-
dZ[1]=[dA1[1]σ′(Z1[1])dA2[1]σ′(Z2[1])]
-
db[1]=dZ[1]
-
dw[1]=dZ[1]A[0]T
整理一下:
反向传播:多个样本的计算
和上面已经没什么差别了
只有A和dA初始化时,从单个向量变成多维向量(矩阵)
例如:
dA[3]=∂A[3]∂L=[A1[3](1)−y1(1)A2[3](1)−y2(1)A1[3](2)−y1(2)A2[3](2)−y2(2)......A1[3](n)−y1(n)A2[3](n)−y2(n)]
需要稍微修改db的求法
之前的算法中,我们省略了db[3]=∂Z[3]∂L∂b[3]∂Z[3]中的第二项,因为都是1
后者应该为一个m×1的矩阵,且全为1
对于多个样本,我们这里没有必要引入矩阵计算,建议使用reduce-sum进行求解