深度学习基础
动手学深度学习v2 - https://www.bilibili.com/video/BV18p4y1h7Dr
个人评价是需要有一点基础
本文不会放太多理论的东西
记录一下代码实操即可
理论请移步李宏毅课程的相关笔记
实验代码:cs_note/DeepLearning/D2L/code at main · aoiJays/cs_note (github.com)
前置准备 环境 1 2 3 4 conda create -n d2l-zh python=3.8 pip conda activate d2l-zh pip install -y d2l torch torchvision
Pytorch 这里认为不需要深入太多
可以先看一下Pytorch小土堆的视频,把Pytorch大概的使用方法先学好
有一些细节在后续学习中慢慢扣
张量操作 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 x = torch.arange(12 ) print (x)print (x.shape)print ( x.numel() ) x = x.reshape(2 , 6 ) print (x)print (torch.zeros(3 ,4 ))print (torch.zeros_like(x))print (torch.ones_like(x))x = torch.tensor( [[1 ,2 ,3 ],[4 ,5 ,6. ]] ) print (x)''' tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]) torch.Size([12]) 12 tensor([[ 0, 1, 2, 3, 4, 5], [ 6, 7, 8, 9, 10, 11]]) tensor([[0., 0., 0., 0.], [0., 0., 0., 0.], [0., 0., 0., 0.]]) tensor([[0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0]]) tensor([[1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1]]) tensor([[1., 2., 3.], [4., 5., 6.]]) '''
张量连接 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 x = torch.arange(12. ).reshape(3 ,4 ) y = x + 12 print (torch.cat( (x,y), dim=0 ))print (torch.cat( (x,y), dim=1 ))''' tensor([[ 0., 1., 2., 3.], [ 4., 5., 6., 7.], [ 8., 9., 10., 11.], [12., 13., 14., 15.], [16., 17., 18., 19.], [20., 21., 22., 23.]]) tensor([[ 0., 1., 2., 3., 12., 13., 14., 15.], [ 4., 5., 6., 7., 16., 17., 18., 19.], [ 8., 9., 10., 11., 20., 21., 22., 23.]]) '''
内存操作
clone detach view reshape 相关原理 留个坑
可使用原地操作避免内存开销
1 2 3 4 5 6 7 8 9 10 11 x = torch.arange(12. ).reshape(3 ,4 ) before = id (x) x = x + 12 print (before == id (x))x = torch.arange(12. ).reshape(3 ,4 ) before = id (x) x[:] = x + 12 print (before == id (x))
正常的赋值是浅拷贝
1 2 3 4 5 6 7 8 9 10 11 12 x = torch.arange(12. ).reshape(3 ,4 ) y = x y += 10 print (id (x), id (y))print (x)''' 140487227237984 140487227237984 tensor([[10., 11., 12., 13.], [14., 15., 16., 17.], [18., 19., 20., 21.]]) '''
深拷贝
1 2 3 4 5 6 7 8 9 10 11 12 13 x = torch.arange(12. ).reshape(3 ,4 ) y = x.clone() y += 10 print (id (x), id (y))print (x)""" 140487208885264 140487208893344 tensor([[ 0., 1., 2., 3.], [ 4., 5., 6., 7.], [ 8., 9., 10., 11.]]) """
梯度 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 x = torch.arange(4. ) print (x, x.requires_grad)x = x.requires_grad_(True ) print (x)y = torch.dot(x, x) print (y)print (x.grad)y.backward() print (x.grad)print ( x.grad == 2 * x )x.grad.zero_() print (x.grad)''' tensor([0., 1., 2., 3.]) False tensor([0., 1., 2., 3.], requires_grad=True) tensor(14., grad_fn=<DotBackward0>) None tensor([0., 2., 4., 6.]) tensor([True, True, True, True]) tensor([0., 0., 0., 0.]) '''
线性回归与优化器 线性模型 y = ∑ w i x i + b y = \sum w_i x_i + b
y = ∑ w i x i + b
可以理解为单层的神经网络
平方损失 L ( y , y ^ ) = 1 2 ∣ y − y ^ ∣ 2 L(y, \hat y) = \frac{1}{2}|y- \hat y|^2
L ( y , y ^ ) = 2 1 ∣ y − y ^ ∣ 2
训练目标 我们对于训练数据X X X y y y
L ( X , y , w , b ) = 1 2 n ( y − X w − b ) 2 L(X,y,w,b) = \frac{1}{2n}(y - Xw-b )^2
L ( X , y , w , b ) = 2 n 1 ( y − X w − b ) 2
我们需要找到最佳的参数w , b w,b w , b
事实上这是一个凸函数,我们甚至可以直接通过梯度为0,求出最优解:
∂ L ∂ w = 1 n ( y − X w ) T X = 0 w ∗ = ( X T X ) − 1 X y \frac{\partial L}{\partial w} = \frac{1}{n}(y-Xw)^TX = 0 \\
w^* = (X^TX)^{-1}Xy
∂ w ∂ L = n 1 ( y − X w ) T X = 0 w ∗ = ( X T X ) − 1 X y
优化方法 - 梯度下降 直接矩阵计算效率实在是太低了,我们需要引入一些优美的优化方法——梯度下降
w t = w t − 1 − η ∂ L ∂ w t − 1 w_t = w_{t-1}- \eta \frac{\partial L}{\partial w_{t-1}}
w t = w t − 1 − η ∂ w t − 1 ∂ L
我们一般不会选择整个数据集进行梯度下降
随机选取一个batch大小的子集,进行一次梯度下降——小批量随机梯度下降法
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 import torchfrom torch import nnimport numpy as npfrom torch.utils import datafrom d2l import torch as d2ltrue_w = torch.tensor([2 , -3.4 ]) true_b = torch.tensor([4.2 ]) features, labels = d2l.synthetic_data(true_w, true_b, 1000 ) dataset = data.TensorDataset( *(features, labels ) ) ''' * 解包运算符 print( *(1,1), (1,1)) 1 1 (1, 1) ''' batch_size = 10 dataLoder = data.DataLoader(dataset, batch_size, shuffle=True ) net = nn.Sequential( nn.Linear(2 , 1 ) ) net[0 ].weight.data.normal_(0 , 0.01 ) net[0 ].bias.data.fill_(0 ) loss = nn.MSELoss() trainer = torch.optim.SGD(net.parameters(), lr=0.03 ) num_epochs = 3 for epoch in range (num_epochs): for X,y in dataLoder: l = loss(y, net(X)) trainer.zero_grad() l.backward() trainer.step() l = loss(net(features), labels) print ( f'epoch {epoch + 1 } , loss {l:f} ' ) print (net[0 ].weight.data)print (net[0 ].bias.data)''' epoch 1 , loss 0.000109 epoch 2 , loss 0.000109 epoch 3 , loss 0.000110 tensor([[ 2.0001, -3.4007]]) tensor([4.2004]) '''
逻辑回归 Softmax 记o i o_i o i i i i
y = softmax ( o ) y ^ i = exp ( o i ) ∑ k exp ( o k ) y = \text{softmax}(o) \\
\hat y_i = \frac{\exp(o_i)}{\sum_k\exp(o_k)}
y = softmax ( o ) y ^ i = ∑ k exp ( o k ) exp ( o i )
交叉熵 我们用交叉熵用于衡量两个概率的区别
H ( p , q ) = ∑ − p i log q i H(p,q) = \sum - p_i \log q_i
H ( p , q ) = ∑ − p i log q i
则对于分类问题,我们可以把损失函数定义为:
L ( y , y ^ ) = H ( y , y ^ ) = ∑ − y i log y ^ i L(y,\hat y) = H(y, \hat y) = \sum - y_i \log \hat y_i
L ( y , y ^ ) = H ( y , y ^ ) = ∑ − y i log y ^ i
并且梯度非常容易计算:
∂ L ∂ o i = softmax ( o ) i − y i \frac{\partial L}{\partial o_i} = \text{softmax}(o)_i - y_i
∂ o i ∂ L = softmax ( o ) i − y i
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 import torchimport torch.nn as nnimport torch.optim as optimimport torchvisionimport torchvision.transforms as transformsfrom torch.utils.data import DataLoadertrans = transforms.Compose([ transforms.ToTensor() ]) train_dataset = torchvision.datasets.FashionMNIST(root="./data" , train=True , transform=trans, download=True ) test_dataset = torchvision.datasets.FashionMNIST(root="./data" , train=False , transform=trans, download=True ) train_loader = DataLoader(train_dataset, batch_size=64 , shuffle=True ) test_loader = DataLoader(test_dataset, batch_size=len (test_dataset), shuffle=False ) class LogisticRegressionModel (nn.Module): def __init__ (self ): super (LogisticRegressionModel, self ).__init__() self .linear = nn.Linear(28 *28 , 10 ) def forward (self, x ): x = x.view(-1 , 28 *28 ) out = self .linear(x) return out model = LogisticRegressionModel() criterion = nn.CrossEntropyLoss() optimizer = optim.SGD(model.parameters(), lr=0.01 ) num_epochs = 10 for epoch in range (num_epochs): model.train() for images, labels in train_loader: outputs = model(images) loss = criterion(outputs, labels) optimizer.zero_grad() loss.backward() optimizer.step() model.eval () with torch.no_grad(): correct = 0 total = 0 for images, labels in test_loader: outputs = model(images) loss = criterion(outputs, labels) _, predicted = torch.max (outputs.data, 1 ) total += labels.size(0 ) correct += (predicted == labels).sum ().item() print (f'Epoch [{epoch+1 } /{num_epochs} ], Loss: {loss.item():.4 f} ' ) print (f'Accuracy of the model on the test images: {100 * correct / total} %' )
多层感知机 感知机 o = sign ( w x + b ) o = \text{sign}(wx+b)
o = sign ( w x + b )
对于正类输出1,负类输出-1
表示了使用一个超平面对空间进行切分
当数据是线性不可分时很难使用
考虑组合多个感知机
MLP 激活函数使得多个线性感知机变成非线性
可以理解为:超平面发生扭曲
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class MLP (nn.Module): def __init__ (self ): super (MLP, self ).__init__() self .fc1 = nn.Linear(28 *28 , 28 *28 ) self .fc2 = nn.Linear(28 *28 , 10 ) self .ReLU = nn.ReLU() def forward (self, x ): x = x.view(-1 , 28 *28 ) x = self .fc1(x) x = self .ReLU(x) x = self .fc2(x) x = self .ReLU(x) return x
对于Pytorch部分,增加几层即可
由于模型变复杂,拟合的开销和批次需要更多
但是最后的表现可以变好
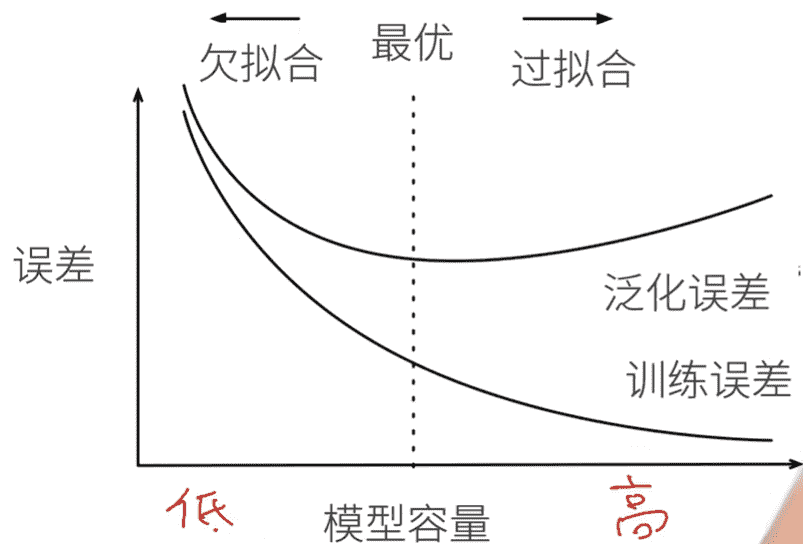
杂谈 误差
训练误差:训练数据上的误差
泛化误差:在新数据上的误差
验证数据:用于验证模型的训练,超参数的选择
测试数据:完全未知的数据,一般只会用来测试一次
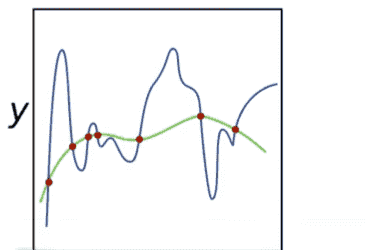
拟合
模型容量估计(需要同种类模型)
VC维
能够完美分类的最大数据样本数量
2维感知机:VC=3,即任意3个点都是线性可分,4个点可能出现xianxingbukef
N维感知机:VC=N+1
一些多层感知机:VC= O ( n log n ) = O(n\log n) = O ( n log n )
但一般没什么用
权重衰退(正则化) 我们可以考虑控制模型参数值的范围,从而控制模型的容量(复杂度)
我们相当于压缩了y y y
min L ( w , b ) subject to ∥ w ∥ 2 ≤ θ \min L(w, b) \text{\quad subject to} \left \| w \right \| ^2 \leq \theta
min L ( w , b ) subject to ∥ w ∥ 2 ≤ θ
min L ( w , b ) + λ 2 ∥ w ∥ 2 \min L(w,b) + \frac{\lambda }{2} \left \| w \right \| ^2
min L ( w , b ) + 2 λ ∥ w ∥ 2
计算梯度:
∂ ( L + λ 2 ∥ w ∥ 2 ) ∂ w = ∂ L ∂ w + λ w \frac{\partial (L+ \frac{\lambda }{2} \left \| w \right \| ^2)}{\partial w} = \frac{\partial L}{\partial w} + \lambda w
∂ w ∂ ( L + 2 λ ∥ w ∥ 2 ) = ∂ w ∂ L + λ w
参数优化:
w t = ( 1 − λ η ) w t − 1 − η ∂ L ∂ w t − 1 w_t = (1-\lambda\eta)w_{t-1}- \eta \frac{\partial L}{\partial w_{t-1}}
w t = ( 1 − λ η ) w t − 1 − η ∂ w t − 1 ∂ L
λ = 0 \lambda=0 λ = 0 η λ < 1 \eta\lambda < 1 η λ < 1
1 2 3 4 5 6 7 8 9 10 11 12 optimizer = optim.SGD(model.parameters(), lr=0.01 , weight_decay=0.01 ) l1_reg = torch.tensor(0. ) for param in model.parameters(): l1_reg += torch.norm(param, p=1 ) total_loss = loss + 0.01 * l1_reg
事实上优化幅度也不大,会更加推荐dropout
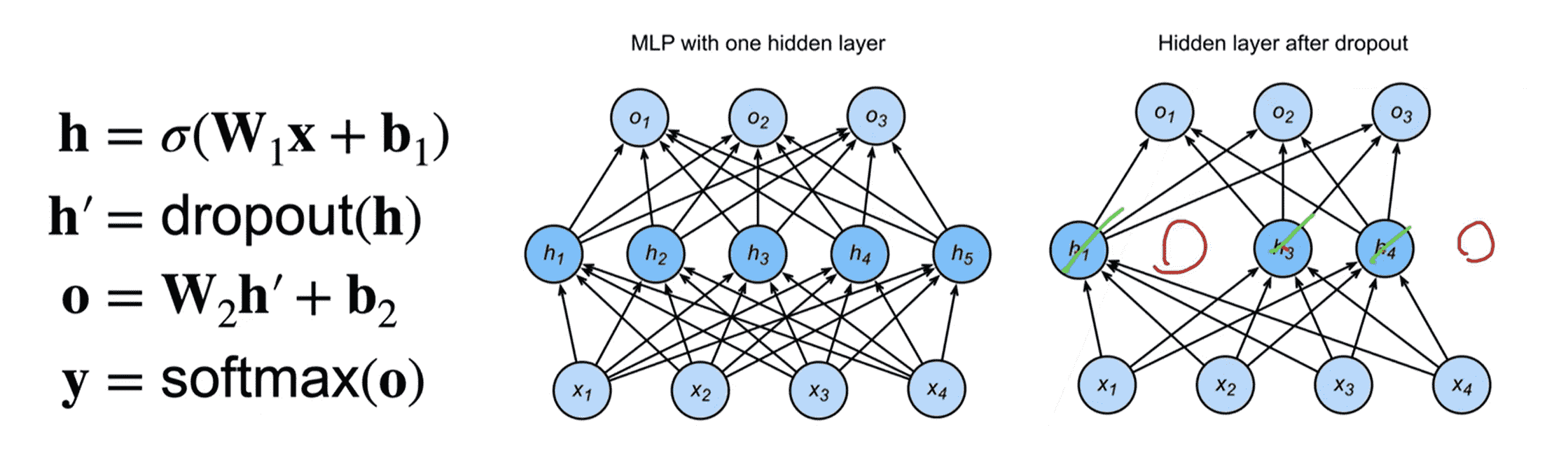
丢弃法(Dropout) 对于x x x x ′ x' x ′ E ( x ′ ) = x E(x') = x E ( x ′ ) = x
我们可以定义dropout函数:
x i ′ = dropout ( x i ) = { 0 with probablity p x i 1 − p otherwise x_i' = \text{dropout}(x_i) = \left\{\begin{matrix}
0 & \text{with probablity p}
\\
\frac{x_i}{1-p} & \text{otherwise}
\end{matrix}\right.
x i ′ = dropout ( x i ) = { 0 1 − p x i with probablity p otherwise
则期望
E ( x i ′ ) = 0 × p + x i 1 − p × ( 1 − p ) = x i E(x_i') = 0 \times p + \frac{x_i}{1-p} \times (1-p) = x_i
E ( x i ′ ) = 0 × p + 1 − p x i × ( 1 − p ) = x i
在训练过程中,我们考虑在隐藏层的输出 中引入dropout
即会失活一些隐藏层节点
dropout的引入目的是通过正则项、噪声,抑制过拟合,增加鲁棒性
因此我们只需要在训练过程中引入即可
对于推理阶段:
h = dropout ( h ) h = \text{dropout}(h)
h = dropout ( h )
即不发生变化
手动实现版本:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def Dropout (X, dropout ): assert 0 <= dropout <= 1 if dropout == 0 : return X if dropout == 1 : return torch.zeros_like(X) mask = (torch.randn(X.shape) > dropout).float () return X * mask / (1.0 - dropout)
Pytorch版本:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class MLP (nn.Module): def __init__ (self ): super (MLP, self ).__init__() self .fc1 = nn.Linear(28 *28 , 28 *28 ) self .fc2 = nn.Linear(28 *28 , 10 ) self .ReLU = nn.ReLU() self .dropout = nn.Dropout(p = 0.3 ) def forward (self, x ): x = x.view(-1 , 28 *28 ) x = self .fc1(x) x = self .ReLU(x) x = self .dropout(x) x = self .fc2(x) x = self .ReLU(x) return x
实测效果确实很牛(
数值稳定 网络层数较大,进行反向传播时
梯度爆炸:梯度大于1,梯度累乘溢出
梯度消失:梯度小于1,梯度累乘趋近0
我们希望梯度值在合理的范围:
例如:[ 1 0 − 6 , 1 0 3 ] [10^{-6}, 10^3] [ 1 0 − 6 , 1 0 3 ]
我们可以考虑如下技巧:
ResNet、LSTM中:将乘法转换为加法
梯度归一化、梯度剪裁(若超过边界值,赋值为边界值)
合理的权重初始化
使用合理的激活函数
权重初始化 我们可以考虑使用N ( 0 , 0.01 ) N(0,0.01) N ( 0 , 0 . 0 1 )
但是这只对小网络有效,深层网络没有保证(太绝对了)
我们将每层的输出、梯度看作随机变量
目标:
令h i t h^t_i h i t t t t i i i
正向
E ( h i t ) = 0 E(h^t_i) = 0 E ( h i t ) = 0 V a r ( h i t ) = a Var(h^t_i) = a V a r ( h i t ) = a a a a
反向
E ( ∂ L ∂ h i t ) = 0 E(\frac{\partial L }{\partial h^t_i}) = 0 E ( ∂ h i t ∂ L ) = 0 V a r ( ∂ L ∂ h i t ) = b Var(\frac{\partial L }{\partial h^t_i}) = b V a r ( ∂ h i t ∂ L ) = b V a r ( h i t ) = a Var(h^t_i) = a V a r ( h i t ) = a b b b
具体推导:【动手学深度学习v2李沐】学习笔记09:数值稳定性、模型初始化、激活函数_数值稳定性 + 模型初始化和激活函数【动手学深度学习v2】-CSDN博客
可以得到:
V a r ( h t ) = n t − 1 V a r ( w t ) V a r ( h t − 1 ) V a r ( ∂ L ∂ h t − 1 ) = n t V a r ( w t ) V a r ( ∂ L ∂ h t ) Var(h^t) = n_{t-1}Var(w_t)Var(h^{t-1}) \\
Var(\frac{\partial L}{\partial h^{t-1}}) = n_{t}Var(w_t)Var(\frac{\partial L}{\partial h^{t}})
V a r ( h t ) = n t − 1 V a r ( w t ) V a r ( h t − 1 ) V a r ( ∂ h t − 1 ∂ L ) = n t V a r ( w t ) V a r ( ∂ h t ∂ L )
此时我们保证$n_{t-1}Var(w_t) = 1, n_{t}Var(w_t) = 1 $即可让方差保持不变
但是n t − 1 , n t n_{t-1},n_t n t − 1 , n t
所以我们放松条件:V a r ( w t ) ( n t + n t − 1 ) = 2 Var(w_t)(n_t+n_{t-1}) = 2 V a r ( w t ) ( n t + n t − 1 ) = 2
因此方差为
V a r ( w t ) = 2 ( n t + n t − 1 ) Var(w_t) = \frac{2}{(n_t+n_{t-1})}
V a r ( w t ) = ( n t + n t − 1 ) 2
我们即可以通过上一层与当前层的节点数,确定本层权重的方差
基于给定均值(0)和方差,进行正态分布或均匀分布的随机数产生即可
拓展阅读:PyTorch中的Xavier以及He权重初始化方法解释_pytorch中he初始化-CSDN博客