卷积神经网络
动手学深度学习v2 - https://www.bilibili.com/video/BV18p4y1h7Dr
课程安排 - 动手学深度学习课程 (d2l.ai)
代码:cs_note/DeepLearning/D2L/code at main · aoiJays/cs_note (github.com)
Pytorch补充
有如下代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| import torch
from torch import nn
class Mynn(nn.Module):
def __init__(self):
super().__init__()
self.sequential1 = nn.Sequential(
nn.Conv2d(in_channels=3, out_channels=32, kernel_size=5, padding=2),
nn.MaxPool2d(2),
nn.Conv2d(in_channels=32, out_channels=32, kernel_size=5, padding=2),
nn.MaxPool2d(2),
nn.Conv2d(in_channels=32, out_channels=64, kernel_size=5, padding=2),
nn.MaxPool2d(2),
nn.Flatten(),
nn.Linear(1024, 64),
nn.Linear(64, 10)
)
self.sequential2 = nn.Linear(10,10)
self.classfication = nn.Sequential(
nn.Linear(10,10),
nn.Linear(10,10),
nn.Linear(10,10)
)
mynn = Mynn()
print(mynn)
'''
Mynn(
(sequential1): Sequential(
(0): Conv2d(3, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(2): Conv2d(32, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(3): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(4): Conv2d(32, 64, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(5): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(6): Flatten(start_dim=1, end_dim=-1)
(7): Linear(in_features=1024, out_features=64, bias=True)
(8): Linear(in_features=64, out_features=10, bias=True)
)
(sequential2): Linear(in_features=10, out_features=10, bias=True)
(classfication): Sequential(
(0): Linear(in_features=10, out_features=10, bias=True)
(1): Linear(in_features=10, out_features=10, bias=True)
(2): Linear(in_features=10, out_features=10, bias=True)
)
)
'''
|
参数管理
-
参数访问:
-
mynn.classfication[0].bias
mynn.classfication[0].weight
mynn.classfication[0].state_dict() # 返回指定层权重字典
mynn.classfication[0].weight.grad = None # 也能访问修改梯度
print(mynn.classfication[0].weight.grad)
# 访问所有参数
for name, param in mynn.named_parameters():
print(name)
# 访问指定层所有参数
for name, param in mynn.classfication.named_parameters():
print(name)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
- 权重初始化
- ```python
def xavier(m):
if type(m) == nn.Linear:
nn.init.xavier_uniform_(m.weight)
def init_42(m):
if type(m) == nn.Linear:
nn.init.constant_(m.weight, 42)
mynn.classfication[0].apply(xavier)
mynn.classfication[1].apply(init_42)
print(mynn.classfication[0].weight.data)
print(mynn.classfication[1].weight.data)
|
读写文件
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| x = torch.arange(12.)
torch.save(x, 'x.temp')
x2 = torch.load('x.temp')
print(x2)
x,y,z = torch.arange(12.),torch.arange(12.),torch.arange(12.)
torch.save([x,y,z], 'xyz.temp')
x2,y2,z2 = torch.load('xyz.temp')
print(x2,y2,z2,sep='\n')
x,y,z = torch.arange(12.),torch.arange(12.),torch.arange(12.)
dict = {
'x':x, 'y':y, 'z':z
}
torch.save(dict, 'xyz.temp')
res = torch.load('xyz.temp')
print(res)
'''
{'x': tensor([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11.]),
'y': tensor([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11.]),
'z': tensor([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11.])}
'''
|
-
模型参数保存
- 事实上已经知道如何保存字典了,模型参数能以字典存储
1
2
3
| torch.save(mynn.state_dict(), 'mynn.pth')
new_model = Mynn()
new_model.load_state_dict(torch.load('mynn.pth'))
|
GPU管理
1
2
3
4
5
6
7
8
9
10
| print(torch.cuda.device_count())
x = torch.arange(12., device=torch.device('cpu'))
print(x.device)
y = torch.arange(12., device=torch.device(f'cuda:{0}'))
print(y.device)
x = x.cuda()
print(x.device)
|
卷积神经网络
MLP
以猫狗分类为例,一张RGB图片假设有36M像素
我们使用一个单隐藏层(100个节点)的全连接MLP进行预测
参数量:
36×220×100≈3.6×108
事实上世界上所有的猫和狗的数量加起来也不到一个亿(不如全部记住)
MLP->卷积层
我们从最开始的MLP开始推导
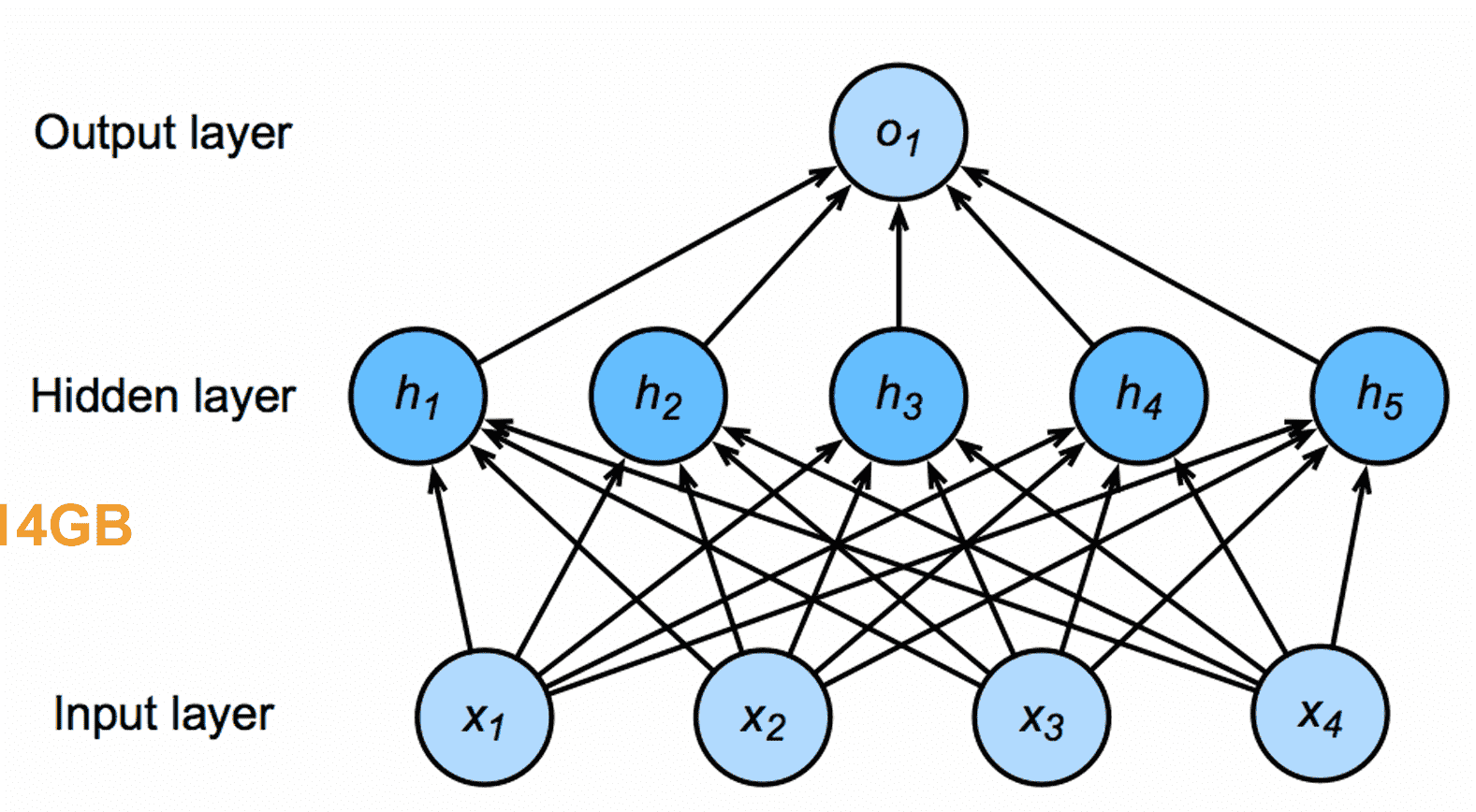
对于一般的MLP,我们会把图片像素全部展成一维张量x
此时则有:
hi=j∑wi,jxj
但是这样显然会丢失二维图像中的上下左右位置的信息
我们考虑将图像、隐藏层变成二维的形式
hi,j=k,l∑wi,j,k,lxk,l
为了方便,我们用相对坐标a,b表示对应的像素
hi,j=k,l∑wi,j,k,lxk,l=a,b∑wi,j,i+a,j+bxi+a,j+b
令vi,j,a,b=wi,j,i+a,j+b
hi,j=a,b∑vi,j,a,bxi+a,j+b
图像的特征有两个原则:
首先是平移不变性,我们假设这套权重v用于提取某一种特征
那么不管i,j是多少,其只跟计算范围内的相对位置有关
即:vi,j,a,b=va,b
根据局部性,我们没必要遍历整个图像, 而是一个非常小的区域(感受野)
我们只遍历相对位置Δ范围内的图像像素(等价于超出范围设置权重为0)
则有:
hi,j=a=−Δ∑Δb=−Δ∑Δva,bxi+a,j+b
这就是二维卷积,相当于使用2Δ×2Δ大小的卷积核,扫一遍图像
多通道
池化层
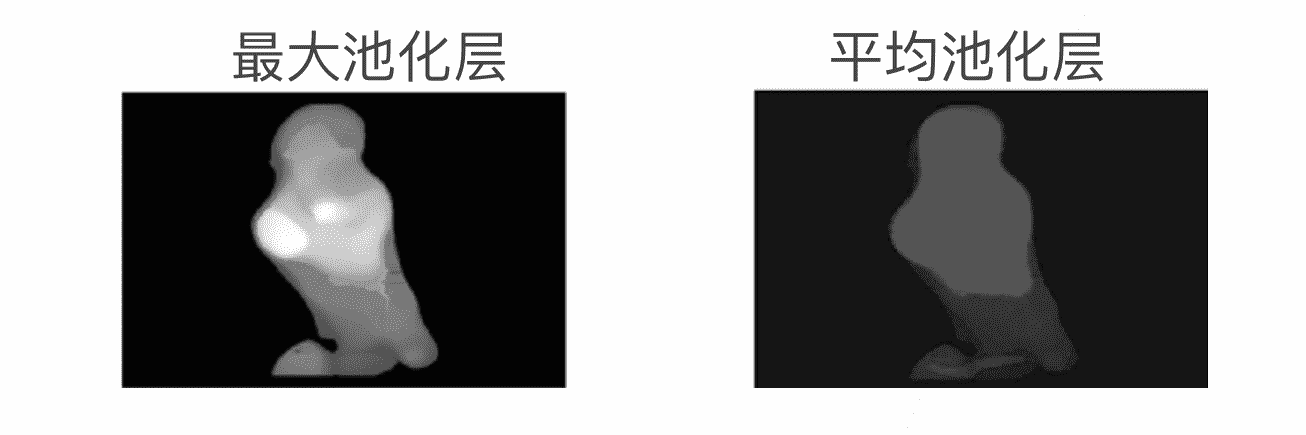
池化层压缩图片分辨率
- 最大池化:某种程度上有放大信号的功能
- 平均池化:更加平滑
经典卷积神经网络
LeNet
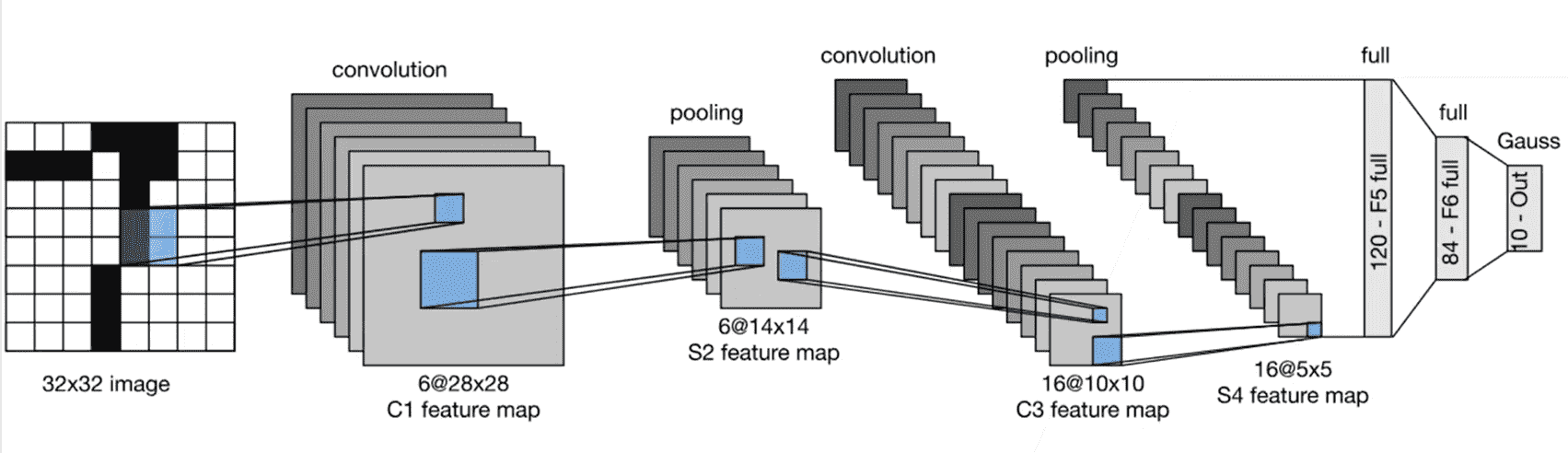
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class LeNet(nn.Module):
def __init__(self) -> None:
super().__init__()
self.Lenet = nn.Sequential(
nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, padding=2),
nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(in_channels=16, out_channels=120, kernel_size=5),
nn.Flatten(),
nn.Linear(120, 84),
nn.Linear(84, 10)
)
def forward(self, x):
return self.Lenet(x)
|
AlexNet
相比于LeNet,引入了新的激活函数:ReLU
从而使得网络可以变得更深
除此之外引入了Dropout和Max Pooling(LeNet是平均池化)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
class AlexNet(nn.Module):
def __init__(self) -> None:
super().__init__()
self.Conv1 = nn.Sequential(
nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
)
self.Conv2 = nn.Sequential(
nn.Conv2d(96, 256, kernel_size=5, padding=2),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
)
self.Conv3 = nn.Sequential(
nn.Conv2d(256, 384, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(384, 384, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(384, 256, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
)
self.mlp = nn.Sequential(
nn.Flatten(),
nn.Linear(6400, 4096), nn.ReLU(), nn.Dropout(p=0.5),
nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(p=0.5),
nn.Linear(4096, 10)
)
def forward(self, x):
x = self.Conv1(x)
x = self.Conv2(x)
x = self.Conv3(x)
x = self.mlp(x)
return x
|
VGG
Alex过于抽象,没有规律
- 堆叠更多窄的卷积核,加深深度效果貌似会更好
- 以VGG块为单位,更方便进行拓展
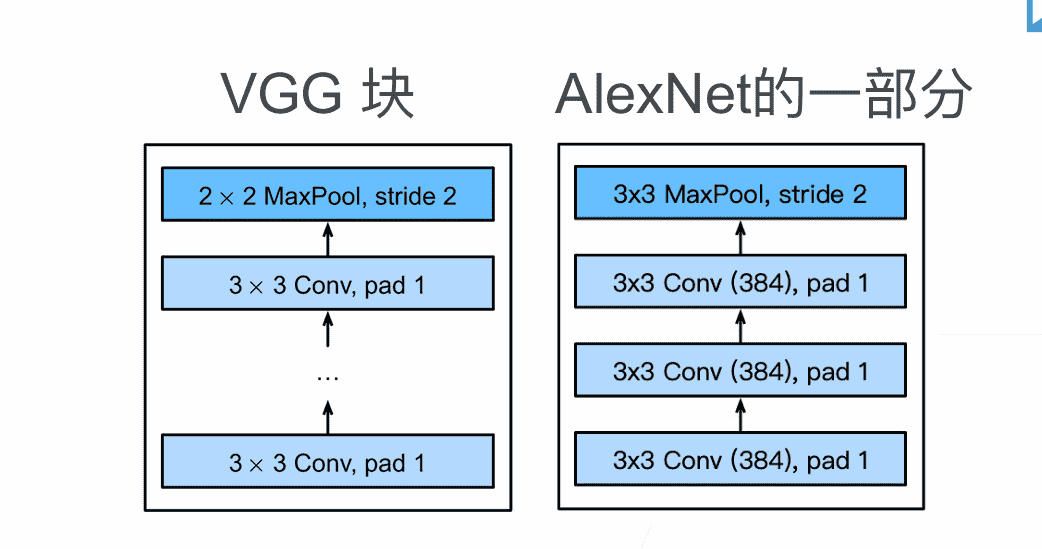
对于一个VGG块,其结构可以用三个参数描述:
in_channelsout_channelsnum_convs:卷积层数量
最后加一层池化层即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| def vgg_block(num_convs, in_channels, out_channels):
layer = []
for i in range(num_convs):
layer.append( nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1 ))
layer.append( nn.ReLU() )
in_channels = out_channels
layer.append( nn.MaxPool2d(kernel_size=2, stride=2) )
return nn.Sequential( * layer )
mynn = vgg_block(3, 4, 8)
print(mynn)
'''
Sequential(
(0): Conv2d(4, 8, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU()
(2): Conv2d(8, 8, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(3): ReLU()
(4): Conv2d(8, 8, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(5): ReLU()
(6): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
'''
|
接下来我们需要去组合VGG块,使用一个列表即可进行定义
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
def vgg_net( conv_arch ):
block_list = []
in_channels = 1
for num_convs, out_channels in conv_arch:
block_list.append( vgg_block(num_convs, in_channels, out_channels) )
in_channels = out_channels
block_list.append(
nn.Sequential(
nn.Flatten(),
nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(), nn.Dropout(0.5),
nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(0.5),\
nn.Linear(4096, 10))
)
return nn.Sequential( * block_list )
conv_arch = ((1, 16), (1, 32), (2, 64), (2, 128), (2, 128))
mynn = vgg_net(conv_arch)
print(mynn)
|
NetWork In NetWork(NiN)
上述网络中都使用了MLP,能够得到更高的抽象,泛化能力更强
在卷积层后的一个全连接层,参数数量非常大
我们希望在不丢弃MLP带来的非线性的情况下,能用较小的参数量进行训练
对于NiN,每个NiN块就是一个小的网络
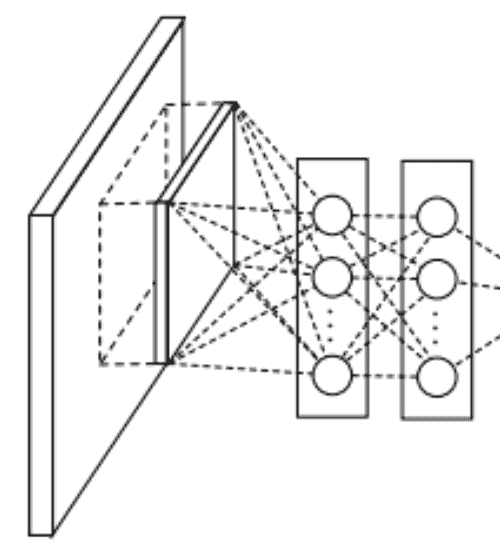
如图,NiN设计为:先过一次卷积层,然后连续过两个全连接层
我们考虑转化全连接层,替换成两次1×1的卷积层
为什么1×1的卷积层可以带来MLP的效果
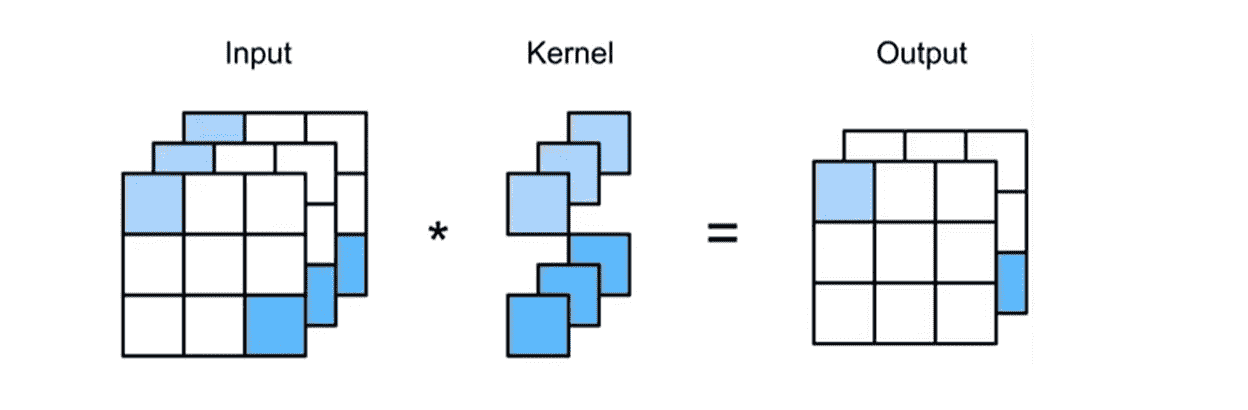
这个时候我们应该这样理解:一个通道是一个神经元
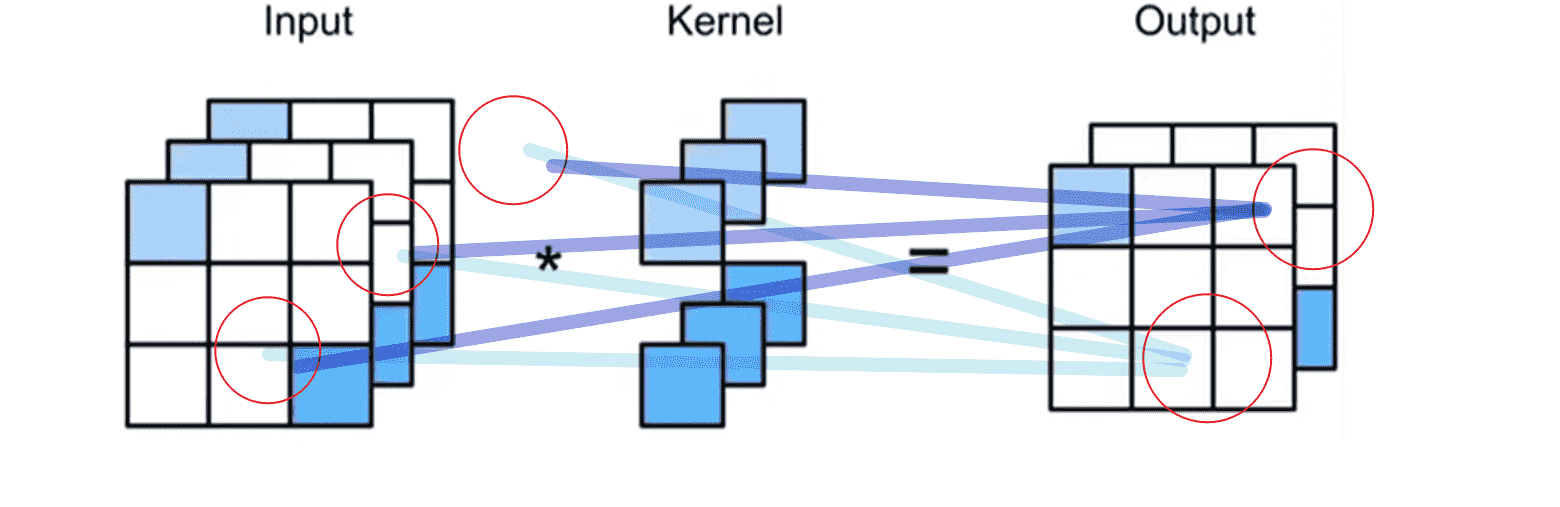
Output层的两组参数,刚好对应上了两个卷积核的参数
因此我们实际上对于通道之间进行了MLP,并且可以自由控制神经元的增加与减少(卷积神经网络的升维和降维)
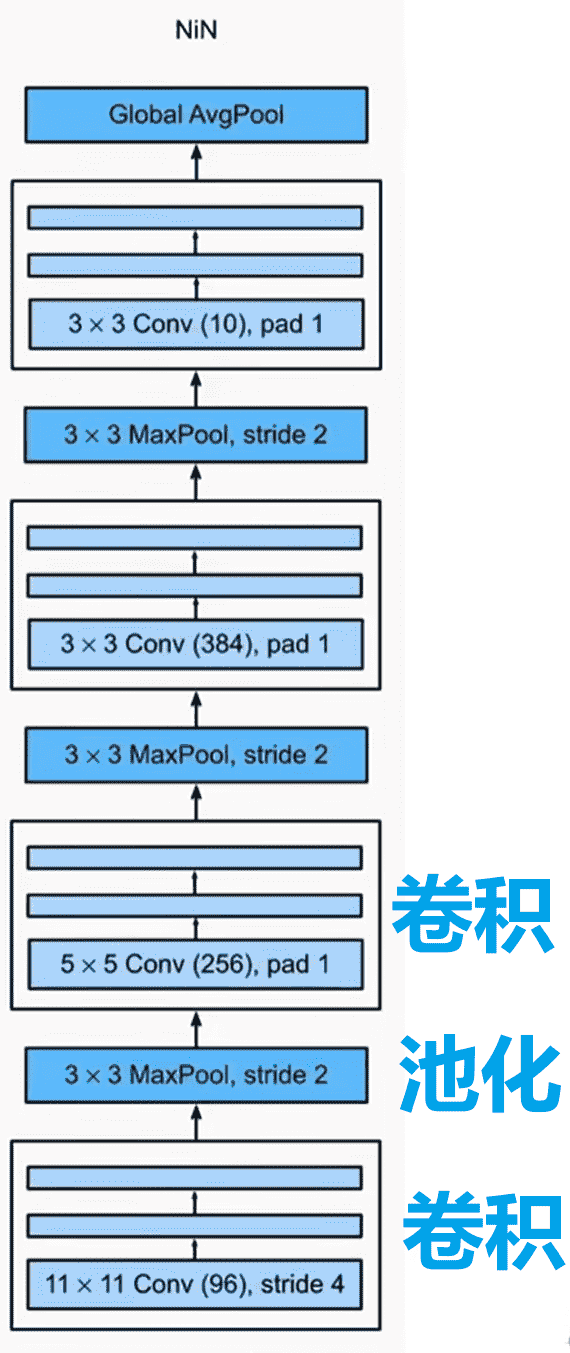
那么我们最后如何输出类别的概率呢?不使用MLP的情况下
我们都知道一个通道是一个神经元了,所以要求最后的通道数 = 类别数
然后我们用全局平均池化,用一个通道的所有值的平均值,作为这个通道(神经元)的输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class NiN(nn.Module):
def NiN_block(self, in_channels, out_channels, kernel_size, strides, padding):
return nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding), nn.ReLU(),
nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU()
)
def __init__(self) -> None:
super().__init__()
self.net = nn.Sequential(
self.NiN_block(1, 96, kernel_size=11, strides=4, padding=0),
nn.MaxPool2d(3, stride=2),
self.NiN_block(96, 256, kernel_size=5, strides=1, padding=2),
nn.MaxPool2d(3, stride=2),
self.NiN_block(256, 384, kernel_size=3, strides=1, padding=1),
nn.MaxPool2d(3, stride=2), nn.Dropout(0.5),
self.NiN_block(384, 10, kernel_size=3, strides=1, padding=1),
nn.AdaptiveAvgPool2d((1, 1)),
nn.Flatten()
)
def forward(self, x):
x = self.net(x)
return x
|
NiN其实很少使用
但是其使用1×1的卷积降低通道数,从而减少参数量的做法非常通用
GoogLeNet
引入Inception块的概念
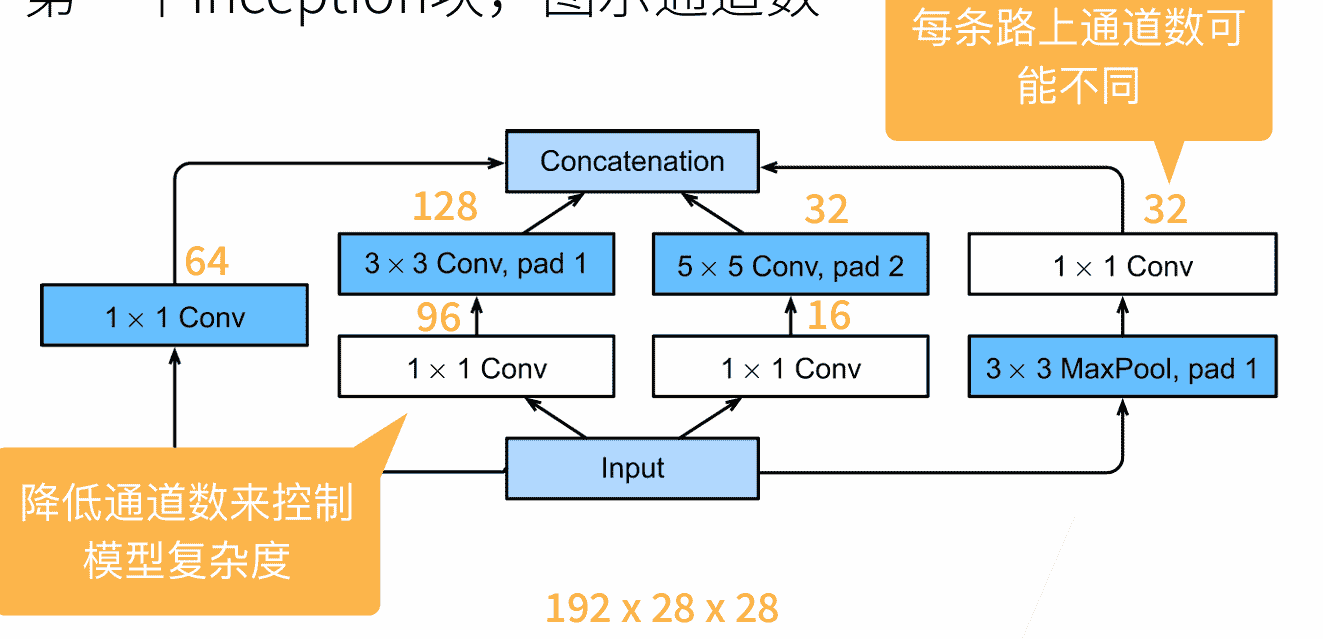
- 不比较哪种卷积效果好,直接组合多个路线所生成的通道(越来越像MLP)
- 大量使用1×1卷积控制了通道数量
- 用较小的参数数量,实现了更深、更快的网络
有100+层,代码就不写了
批量归一化batch normalization
- 越底层的梯度越小,更新越慢
- 底层一但更新,高层也需要重新训练
- 重复训练,收敛速度慢
- 可以看作一个层(BN层)
对于当前层,如果我们在这层之前插入了一个BN层,就需要对其输入xi进行处理
我们考虑像数值稳定性一样,固定每层的输出、梯度的数值分布
对于一个Batch:
μB=∣B∣1i∈B∑xiσB2=∣B∣1i∈B∑(xi−μB)2+ϵ
ϵ是一个很小的数,避免方差为0
接下来修改所有xi
xi′=γσBxi−μB+β
其中有两个参数γ,β是这层中的可学习的参数
若分布不合适,会通过学习调整分布
理论上BN层应该放在激活函数之前
BN是一个线性变化,而激活函数是一个非线性变化
我们最好是线性变化完再进行非线性
但是似乎放在激活函数之后更有效Batch-normalized 应该放在非线性激活层的前面还是后面? - 知乎 (zhihu.com)
- 全连接层:作用在每个神经元的输出
- 卷积层:作用在每个通道
某种程度上引入了一定的噪声,因此不需要和Dropout一起使用
BN可以加速收敛,但是不会优化模型精度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class LeNet(nn.Module):
def __init__(self) -> None:
super().__init__()
self.Lenet = nn.Sequential(
nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, padding=2),
nn.BatchNorm2d(6),
nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5),
nn.BatchNorm2d(16),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(in_channels=16, out_channels=120, kernel_size=5),
nn.BatchNorm2d(120),
nn.Flatten(),
nn.Linear(120, 84),
nn.BatchNorm1d(84),
nn.Linear(84, 10)
)
def forward(self, x):
return self.Lenet(x)
|
李宏毅:经过归一化,Error Surface会变得平坦,所以可以用大一点的学习率
ResNet
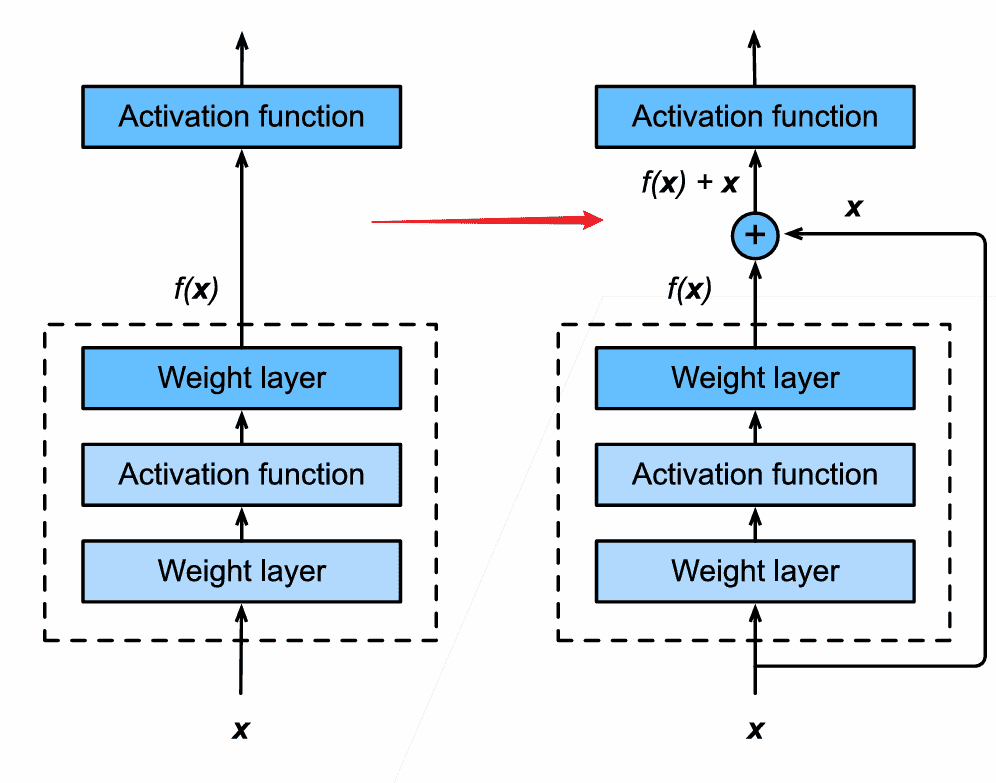
-
相当于接了一条短路线,绕过这一块新加入的网络
- 后续训练时,如果新加入的网络效果很差(没有什么影响),则其梯度会很小,无法更新
- 相当于直接使用x作为主要贡献
- 因此新加入的网络块,有效最好,无效也不会使得网络变坏
-
残差?
- 理论上是先训练一个非常简单的模型(通过短路)
- 再根据残差,得到梯度,去更新可以拓展的网络块
-
为什么ResNet可以训练1000层?
-
主要原因是避免了梯度弥散
-
y=f(x)+g(f(x))∂w∂y=∂w∂f(x)+∂w∂g(f(x))
-
原本会因为累乘导致梯度变小,但是此处是加法(有保底)
-
另一种理解:高层的大梯度会通过短路,送到底层进行优化









