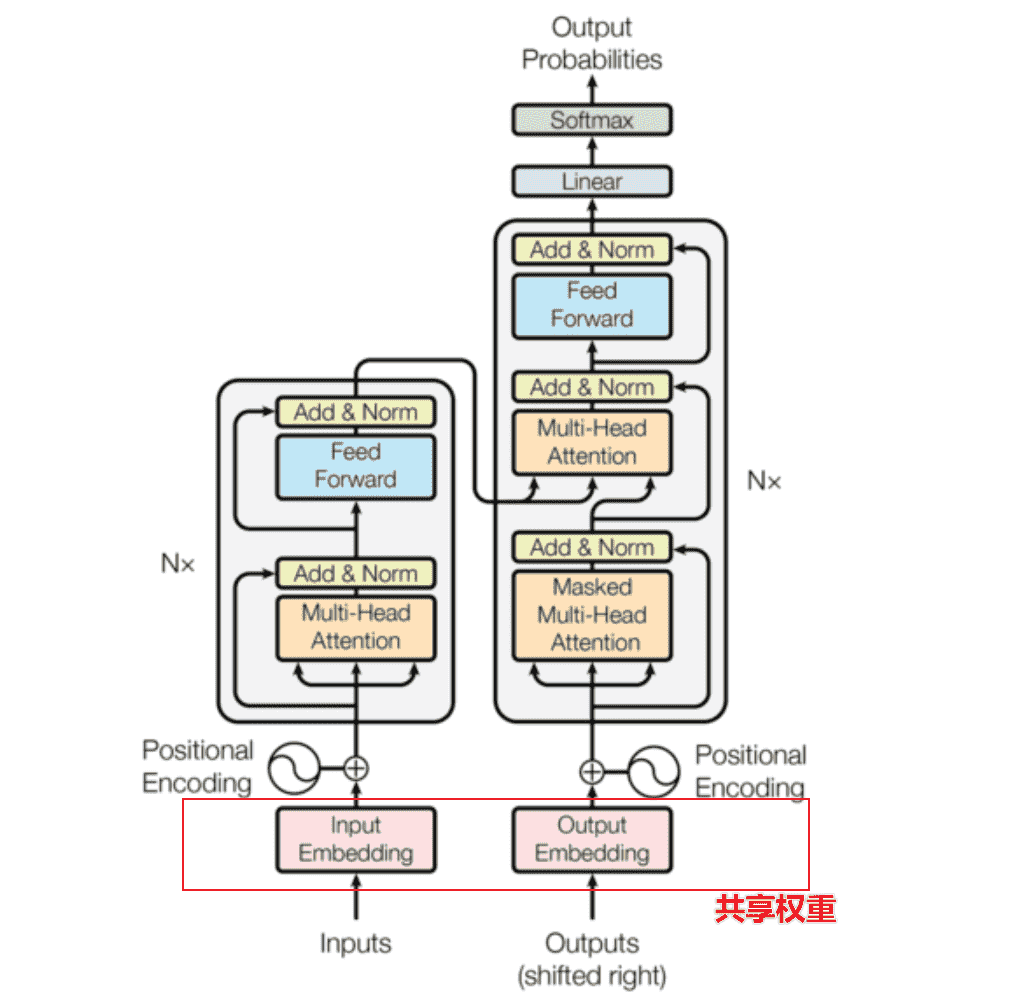
Transformer
理论:李宏毅机器学习L5 · Sequence to Sequence · BiribiriBird’s Gallery (aoijays.top)
参考代码:一文看懂Transformer内部原理(含PyTorch实现) - 郭耀华 - 博客园 (cnblogs.com)
论文:Transformer论文逐段精读【论文精读】_哔哩哔哩_bilibili
其实这里跟动手学深度学习没什么关系了,只有前半部分是
动手学深度学习那的代码看不动了
我发现不如直接翻论文看源代码(
笔记中只有如何构建Transfomer架构的代码
关于训练什么的懒得写了(有用到再补吧(
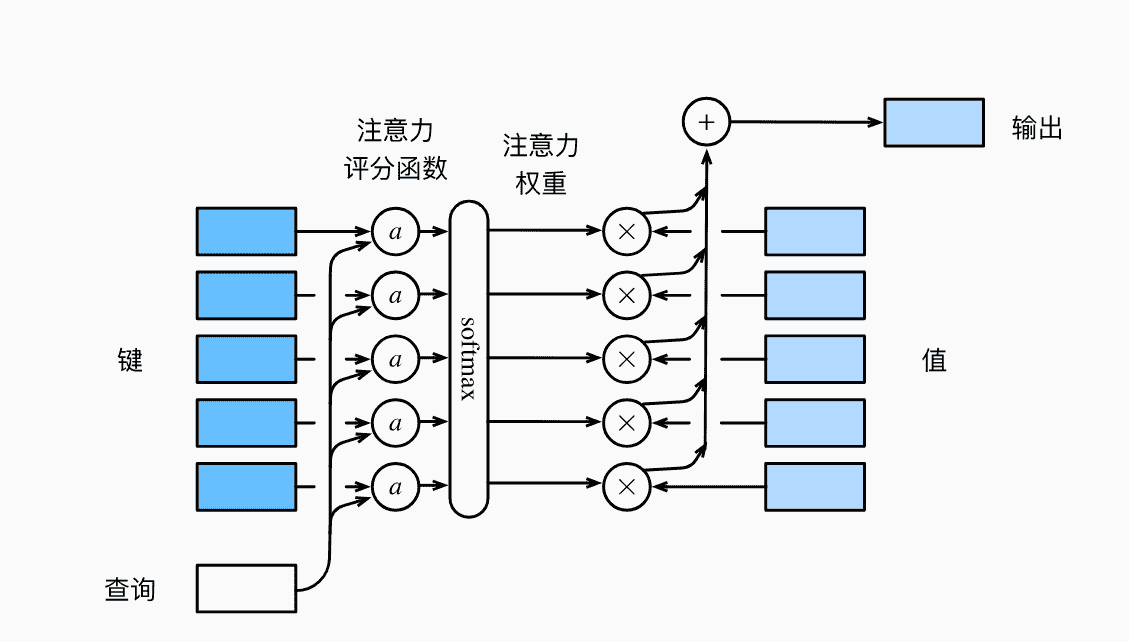
注意力 注意力机制 注意力机制对不同信息的关注程度用权值体现
本质上Attention机制是Source中元素的Value值进行加权求和,而Query和Key用来计算对应Value的权重系数
Attention ( query , Source ) = ∑ Source similarity ( query , key i ) × value i \text{Attention}(\text{query},\text{Source}) = \sum_{}^{\text{Source}} \text{similarity}(\text{query},\text{key}_i)\times \text{value}_i
Attention ( query , Source ) = ∑ Source similarity ( query , key i ) × value i
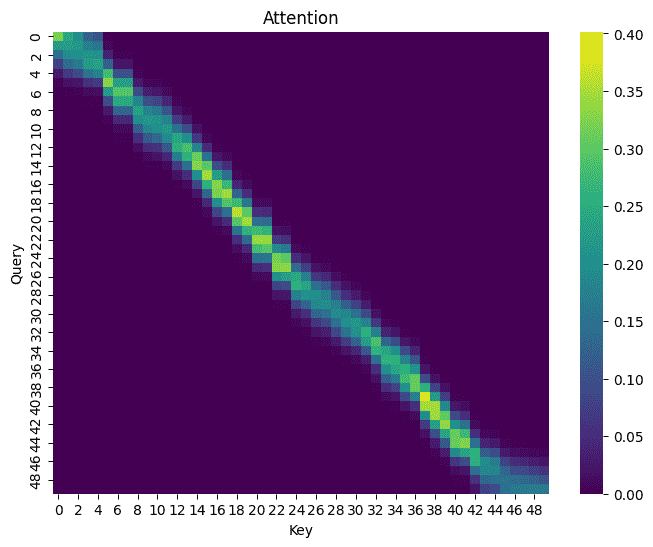
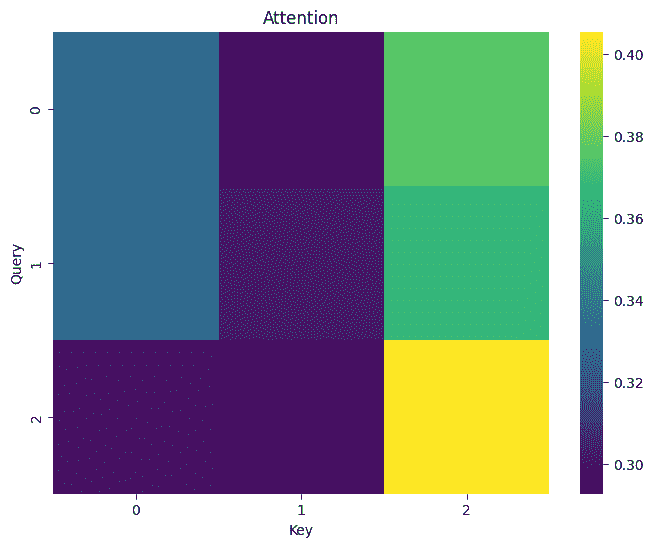
我们可以使用heatmap展示权值
1 2 3 4 5 6 7 8 9 10 def show_heatmaps (matrix ): matrix = matrix.squeeze() plt.figure(figsize=(8 , 6 )) sns.heatmap(matrix,cmap="viridis" ) plt.title("Attention" ) plt.xlabel("Key" ) plt.ylabel("Query" ) plt.show() show_heatmaps(torch.eye(10 ).reshape((1 , 1 , 10 , 10 )))
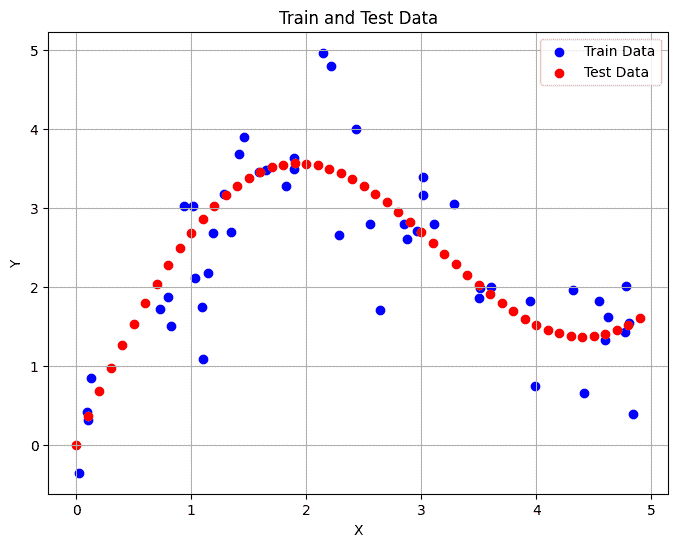
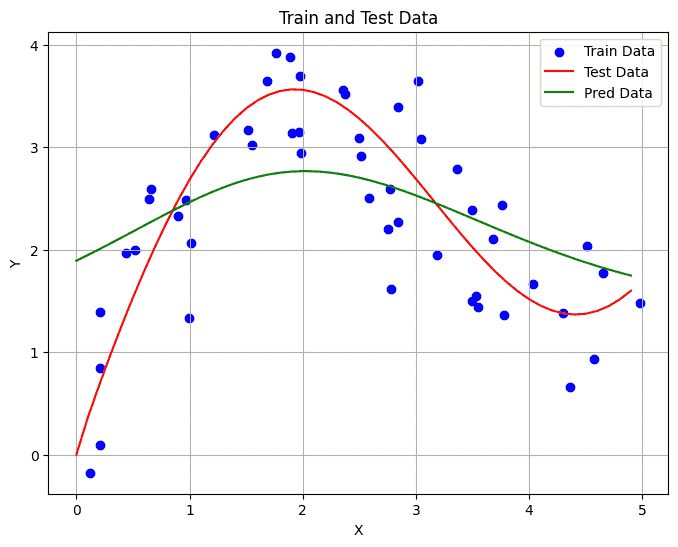
注意力汇聚 我们构造一个符合以下函数的数据集:
y = 2 sin ( x ) + x 0.8 y=2\sin(x)+x^{0.8}
y = 2 sin ( x ) + x 0 . 8
1 2 3 4 5 6 7 8 9 n_train = 50 x_train,_ = torch.sort(torch.rand(n_train) * 5 ) y_train = torch.sin(x_train) * 2 + x_train**0.8 y_train += torch.normal(0 ,0.5 ,(n_train,)) n_test = 50 x_test = torch.arange(0 , 5 , 5 /n_test) y_test = torch.sin(x_test) * 2 + x_test**0.8
绘图代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 def show_line (y_pred=None ): plt.figure(figsize=(8 , 6 )) plt.scatter(x_train, y_train, color='blue' , label='Train Data' ) plt.plot(x_test, y_test, color='red' , label='Test Data' ) if y_pred is None : pass else : plt.plot(x_test, y_pred, color='green' , label='Pred Data' ) plt.title('Train and Test Data' ) plt.xlabel('X' ) plt.ylabel('Y' ) plt.legend() plt.grid(True ) plt.show() show_line()
平均汇聚 比较简单的考虑,对于所有键值对k e y , v a l u e key,value k e y , v a l u e
Attention ( query ) = 1 n ∑ y i \text{Attention}(\text{query}) = \frac{1}{n}\sum y_i
Attention ( query ) = n 1 ∑ y i
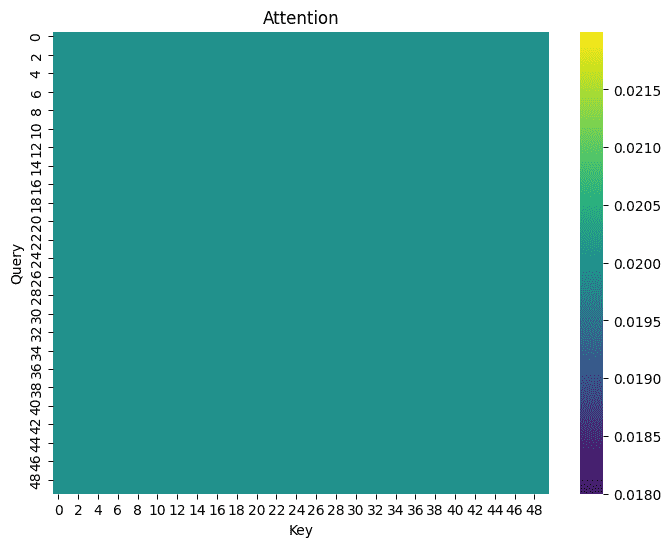
1 2 3 4 5 6 def avg_attention (query, x_train, y_train ): return torch.full( (len (query), len (x_train)), 1 /len (x_train)) attention_weights = avg_attention(x_test, x_train, y_train) show_heatmaps(attention_weights)
显然,所有权重都一样:
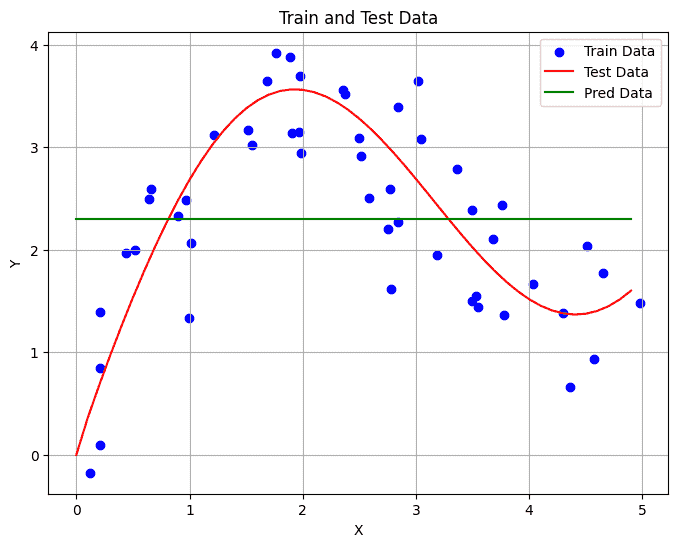
1 2 3 y_pred = torch.matmul(attention_weights, y_train) show_line(y_pred)
显然是不太好,我们并没有考虑key的存在
非参数注意力汇聚 我们希望引入key。query和key越近,权重当然是越大的
Attention ( query ) = ∑ K ( x − x i ) ∑ K ( x − x j ) × y i \text{Attention}(\text{query}) = \sum \frac{K(x-x_i)}{\sum K(x-x_j)} \times y_i
Attention ( query ) = ∑ ∑ K ( x − x j ) K ( x − x i ) × y i
其中K K K
K ( μ ) = 1 2 π exp ( − μ 2 2 ) K(\mu) = \frac{1}{\sqrt{2\pi}}\exp(-\frac{\mu^2}{2})
K ( μ ) = 2 π 1 exp ( − 2 μ 2 )
代入得:
Attention ( query ) = ∑ softmax ( − 1 2 ( x − x i ) 2 ) × y i \text{Attention}(\text{query}) = \sum\text{softmax}(-\frac{1}{2}(x-x_i)^2)\times y_i
Attention ( query ) = ∑ softmax ( − 2 1 ( x − x i ) 2 ) × y i
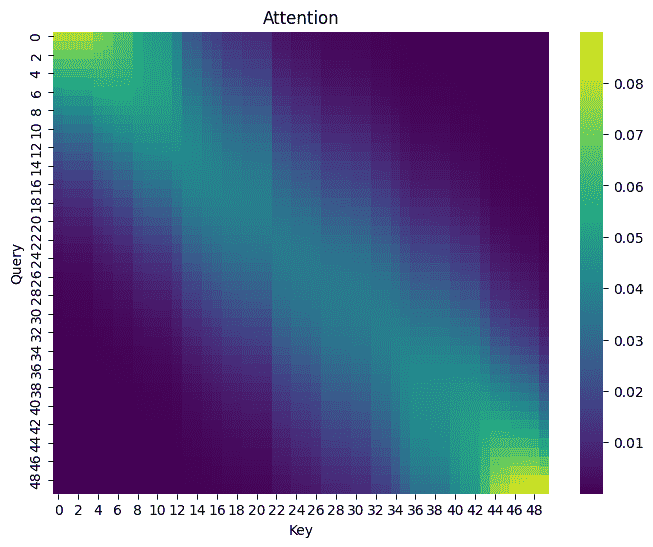
1 2 3 4 5 6 7 8 9 10 def non_param_attention (query, x_train, y_train ): x_repeat = x_train.repeat(len (query)).reshape(len (query),-1 ) x_repeat = -1 /2 * ((x_repeat - query.reshape(-1 ,1 )) ** 2 ) return nn.functional.softmax(x_repeat, dim=1 ) attention_weights = non_param_attention(x_test, x_train, y_train) show_heatmaps(attention_weights) y_pred = torch.matmul(attention_weights, y_train) show_line(y_pred)
好了不少
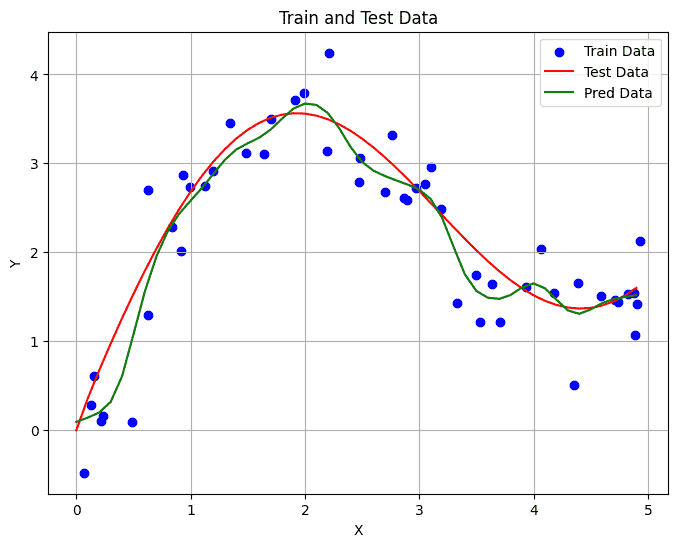
带参数注意力汇聚 可以引入可学习参数,模型自适应地进行调整
Attention ( query ) = ∑ K ( ( x − x i ) × w ) ∑ K ( ( x − x j ) × w ) × y i \text{Attention}(\text{query}) = \sum \frac{K((x-x_i)\times w)}{\sum K((x-x_j)\times w)} \times y_i
Attention ( query ) = ∑ ∑ K ( ( x − x j ) × w ) K ( ( x − x i ) × w ) × y i
同样使用高斯核:
Attention ( query ) = ∑ softmax ( − 1 2 ( ( x − x i ) × w ) 2 ) × y i \text{Attention}(\text{query}) = \sum\text{softmax}(-\frac{1}{2}((x-x_i)\times w)^2)\times y_i
Attention ( query ) = ∑ softmax ( − 2 1 ( ( x − x i ) × w ) 2 ) × y i
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 class Mynn (nn.Module): def __init__ (self, *args, **kwargs ) -> None : super ().__init__(*args, **kwargs) self .w = nn.Parameter(torch.rand((1 ,), requires_grad=True )) self .attention_weights = torch.rand(1 ,) def forward (self, query, x_train, y_train ): x_repeat = (x_train.repeat(len (query)).reshape(len (query),-1 ) - query.reshape(-1 ,1 )) * self .w x_repeat = -1 /2 * ( x_repeat** 2 ) self .attention_weights = nn.functional.softmax(x_repeat, dim=1 ) return torch.matmul(self .attention_weights, y_train) def getAttention (self ): show_heatmaps(self .attention_weights) net = Mynn() loss = nn.MSELoss(reduction='none' ) trainer = torch.optim.SGD(net.parameters(), lr=0.5 ) for epoch in range (5 ): trainer.zero_grad() l = loss(net(x_train, x_train, y_train), y_train) l.sum ().backward() trainer.step() print (f'epoch {epoch + 1 } , loss {float (l.sum ()):.6 f} ' ) ''' epoch 1, loss 57.662407 epoch 2, loss 6.773480 epoch 3, loss 6.629529 epoch 4, loss 6.524448 epoch 5, loss 6.442084 ''' with torch.no_grad(): y_pred = net(x_test, x_train, y_train) show_line(y_pred) net.getAttention()
效果好很多
可以发现权重更加集中,因此受训练数据影响非常大
出现不平滑的曲线
注意力评分函数 我们的权重最后是依靠softmax进行输出
我们把喂入softmax的函数称为注意力评分函数
对于前文来说,评分函数为:
− 1 2 ( ( x − x i ) × w ) 2 -\frac{1}{2}((x-x_i)\times w)^2
− 2 1 ( ( x − x i ) × w ) 2
掩蔽softmax 我们把评分函数这个概念独立出来是有意义的
有时候我们会需要对序列填充词元,但是最后在进行计算时,他们不应该带来权重,即我们需要屏蔽他们
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def masked_softmax (X, valid_lens ): if valid_lens is None : return nn.functional.softmax(X, dim=-1 ) else : shape = X.shape if valid_lens.dim() == 1 : valid_lens = torch.repeat_interleave(valid_lens, shape[1 ]) else : valid_lens = valid_lens.reshape(-1 ) X = sequence_mask(X.reshape(-1 , shape[-1 ]), valid_lens, value=-1e6 ) return nn.functional.softmax(X.reshape(shape), dim=-1 )
测试:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 masked_softmax(torch.rand(2 , 2 , 4 ), torch.tensor([2 , 3 ])) ''' tensor([[[0.5980, 0.4020, 0.0000, 0.0000],# 2 [0.5548, 0.4452, 0.0000, 0.0000]], # 2 [[0.3716, 0.3926, 0.2358, 0.0000], # 3 [0.3455, 0.3337, 0.3208, 0.0000]]]) # 3 ''' masked_softmax(torch.rand(2 , 2 , 4 ), torch.tensor([[1 , 3 ], [2 , 4 ]])) ''' tensor([[[1.0000, 0.0000, 0.0000, 0.0000], # 1 [0.4125, 0.3273, 0.2602, 0.0000]], # 3 [[0.5254, 0.4746, 0.0000, 0.0000], # 2 [0.3117, 0.2130, 0.1801, 0.2952]]]) # 4 '''
加性注意力 有时候查询和键是尺寸不一致的向量
我们可以分别对q , k q,k q , k
定义加性注意力的评分函数:
a ( q , k ) = W v T tanh ( W q q + W k k ) a(q,k) = W_v^T\tanh(W_qq+W_kk)
a ( q , k ) = W v T tanh ( W q q + W k k )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class AdditiveAttention (nn.Module): """加性注意力""" def __init__ (self, key_size, query_size, num_hiddens, dropout, **kwargs ): super (AdditiveAttention, self ).__init__(**kwargs) self .W_k = nn.Linear(key_size, num_hiddens, bias=False ) self .W_q = nn.Linear(query_size, num_hiddens, bias=False ) self .w_v = nn.Linear(num_hiddens, 1 , bias=False ) self .dropout = nn.Dropout(dropout) def forward (self, queries, keys, values, valid_lens ): queries, keys = self .W_q(queries), self .W_k(keys) features = queries.unsqueeze(2 ) + keys.unsqueeze(1 ) features = torch.tanh(features) scores = self .w_v(features).squeeze(-1 ) self .attention_weights = masked_softmax(scores, valid_lens) return torch.bmm(self .dropout(self .attention_weights), values)
缩放点积注意力 我们想计算得更简单一点
那么我们定义评分函数:
a ( q , k ) = q ⋅ k d a(q,k) = \frac{q\cdot k}{\sqrt{d}}
a ( q , k ) = d q ⋅ k
其中d d d
考虑每一个token都是一个服从标准正态分布的随机变量
那么方差都是1,长度为d序列的方差就是d个1相加得到1
所以最后结果除以标准差,缩放一下
自注意力机制 李宏毅机器学习L4 · Sequence as input · BiribiriBird’s Gallery (aoijays.top)
相比循环神经网络,可以做并行化
手搓Transformer 顺序和论文顺序不太一样,因为直接按顺序的话代码看不懂(
Word Embedding 我们需要对词元序列转化为张量
考虑使用nn.Embedding,作为一个可学习 的词嵌入方式
我们可以将词嵌入的结果看作服从标准正态分布的随机变量,我们考虑进行一定的缩放
即乘上一个d m o d e l \sqrt{d_{model}} d m o d e l d_model 的大小成比例
为什么 ?后面需要Position Encoding,两个结果需要相加,但是如果embedding结果比较小,就会被掩盖,因此需要缩放一下
1 2 3 4 5 6 7 8 class Embeddings (nn.Module): def __init__ (self, d_model, vocab ): super ().__init__() self .lut = nn.Embedding(vocab, d_model) self .d_model = d_model def forward (self, x ): return self .lut(x) * math.sqrt(self .d_model)
Position Encoding Transformer中采用的是Sinusoidal Position Encoding
对于序列中位置位于p o s pos p o s d m o d e l d_{model} d m o d e l
2 i 2i 2 i 2 i + 1 2i+1 2 i + 1
P E ( p o s , 2 i ) = sin ( p o s 1000 0 2 i / d m o d e l ) P E ( p o s , 2 i + 1 ) = cos ( p o s 1000 0 2 i / d m o d e l ) PE(pos,2i) = \sin (\frac{pos}{10000^{2i/d_{model}}})\\
PE(pos,2i+1) = \cos (\frac{pos}{10000^{2i/d_{model}}})
P E ( p o s , 2 i ) = sin ( 1 0 0 0 0 2 i / d m o d e l p o s ) P E ( p o s , 2 i + 1 ) = cos ( 1 0 0 0 0 2 i / d m o d e l p o s )
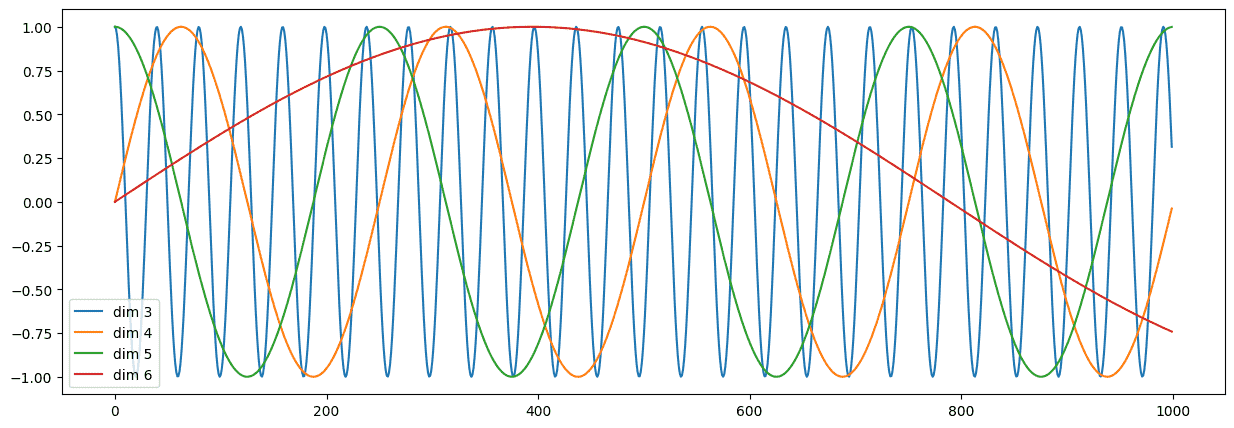
使用正余弦函数交错
对于同一个维度 ,都只是关于p o s pos p o s 1 1 1 1 10000 \frac{1}{10000} 1 0 0 0 0 1 2 π 2\pi 2 π 10000 × 2 π 10000\times 2\pi 1 0 0 0 0 × 2 π
这样的好处是我们可以轻松表示序列中的相对位置
对于p o s pos p o s p o s + k pos+k p o s + k p o s + k pos+k p o s + k
P E ( p o s + k , 2 i ) = sin ( p o s + k 1000 0 2 i / d m o d e l ) PE(pos+k,2i) = \sin (\frac{pos+k}{10000^{2i/d_{model}}})
P E ( p o s + k , 2 i ) = sin ( 1 0 0 0 0 2 i / d m o d e l p o s + k )
令分母为1 w 2 i \frac{1}{w_{2i}} w 2 i 1
P E ( p o s + k , 2 i ) = sin ( w 2 i ( p o s + k ) ) = sin ( w 2 i p o s ) cos ( w 2 i k ) + cos ( w 2 i p o s ) sin ( w 2 i k ) = P E ( p o s , 2 i ) cos ( w 2 i k ) + P E ( p o s , 2 i ) sin ( w 2 i k ) PE(pos+k,2i) = \sin (w_{2i}(pos+k)) \\
= \sin(w_{2i}pos)\cos(w_{2i}k)+\cos(w_{2i}pos)\sin(w_{2i}k)\\
= PE(pos,2i)\cos(w_{2i}k)+PE(pos,2i)\sin(w_{2i}k)
P E ( p o s + k , 2 i ) = sin ( w 2 i ( p o s + k ) ) = sin ( w 2 i p o s ) cos ( w 2 i k ) + cos ( w 2 i p o s ) sin ( w 2 i k ) = P E ( p o s , 2 i ) cos ( w 2 i k ) + P E ( p o s , 2 i ) sin ( w 2 i k )
对于2 i + 1 2i+1 2 i + 1
你会发现p o s + k pos+k p o s + k p o s pos p o s
进一步的,当我们将两个位置的位置编码进行点积,将会得到一个只关于维度i i i k k k
则有:
P E ( p o s + k , ) P E ( p o s ) = P E ( p o s − k ) P E ( p o s ) PE(pos+k,)PE(pos) = PE(pos-k)PE(pos)
P E ( p o s + k , ) P E ( p o s ) = P E ( p o s − k ) P E ( p o s )
两对距离一致的位置编码点积结果一致
坏处是无法区分方向
开始实现代码:
对于第i i i divterm i \text{divterm}_i divterm i
divterm i = 1 1000 0 2 i / d m o d e l = exp ( − ( 2 i / d m o d e l ) ln 1 0 4 ) \text{divterm}_i = \frac{1}{10000^{2i/d_{model}}} = \exp( -(2i/d_{model})\ln 10^4 )
divterm i = 1 0 0 0 0 2 i / d m o d e l 1 = exp ( − ( 2 i / d m o d e l ) ln 1 0 4 )
则第p o s pos p o s 2 i 2i 2 i 2 i + 1 2i+1 2 i + 1 sin ( p o s × divterm i ) , cos ( p o s × divterm i ) \sin(pos\times \text{divterm}_i),\cos(pos\times \text{divterm}_i) sin ( p o s × divterm i ) , cos ( p o s × divterm i )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class PositionalEncoding (nn.Module): def __init__ (self, d_model, dropout, max_len = 5000 ): super (PositionalEncoding, self ).__init__() position_encoding = torch.zeros( max_len, d_model ) div_term = torch.exp( -torch.arange(0 , d_model, 2 ) / d_model * math.log(10000.0 ) ) position = torch.arange( max_len ).unsqueeze(1 ) half_pe = position*div_term position_encoding[:, 0 ::2 ] = torch.sin(half_pe) position_encoding[:, 1 ::2 ] = torch.cos(half_pe) position_encoding = position_encoding.unsqueeze(0 ) self .register_buffer('position_encoding' , position_encoding) self .dropout = nn.Dropout(dropout) def forward (self, x ): return self .dropout( x + self .position_encoding[:, : x.size(1 ) ] )
测试效果:
1 2 3 4 5 6 7 8 plt.figure(figsize=(15 , 5 )) pe = PositionalEncoding(10 , 0 , 1000 ) y = pe((torch.zeros(2 , 1000 , 10 ))) print (y.shape)plt.plot(np.arange(1000 ), y[0 , :, 3 :7 ].data.numpy()) plt.legend(["dim %d" %p for p in [3 ,4 ,5 ,6 ]])
Attention
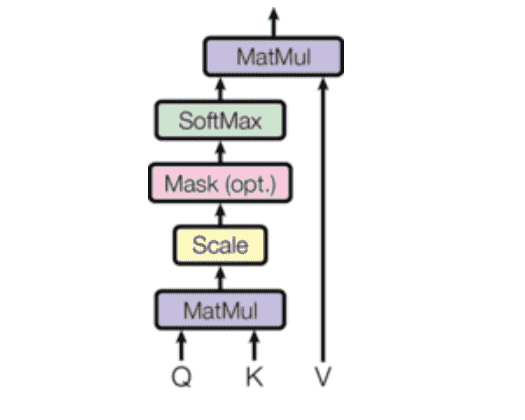
Transformer采用缩放点积注意力机制
前文讲过了
我们将多组q , k , v q,k,v q , k , v Q , K , V Q,K,V Q , K , V
则有:
Attention ( Q , K , V ) = softmax ( Q K T d K ) V \text{Attention}(Q,K,V) = \text{softmax}(\frac{QK^T}{\sqrt{d_K}})V
Attention ( Q , K , V ) = softmax ( d K Q K T ) V
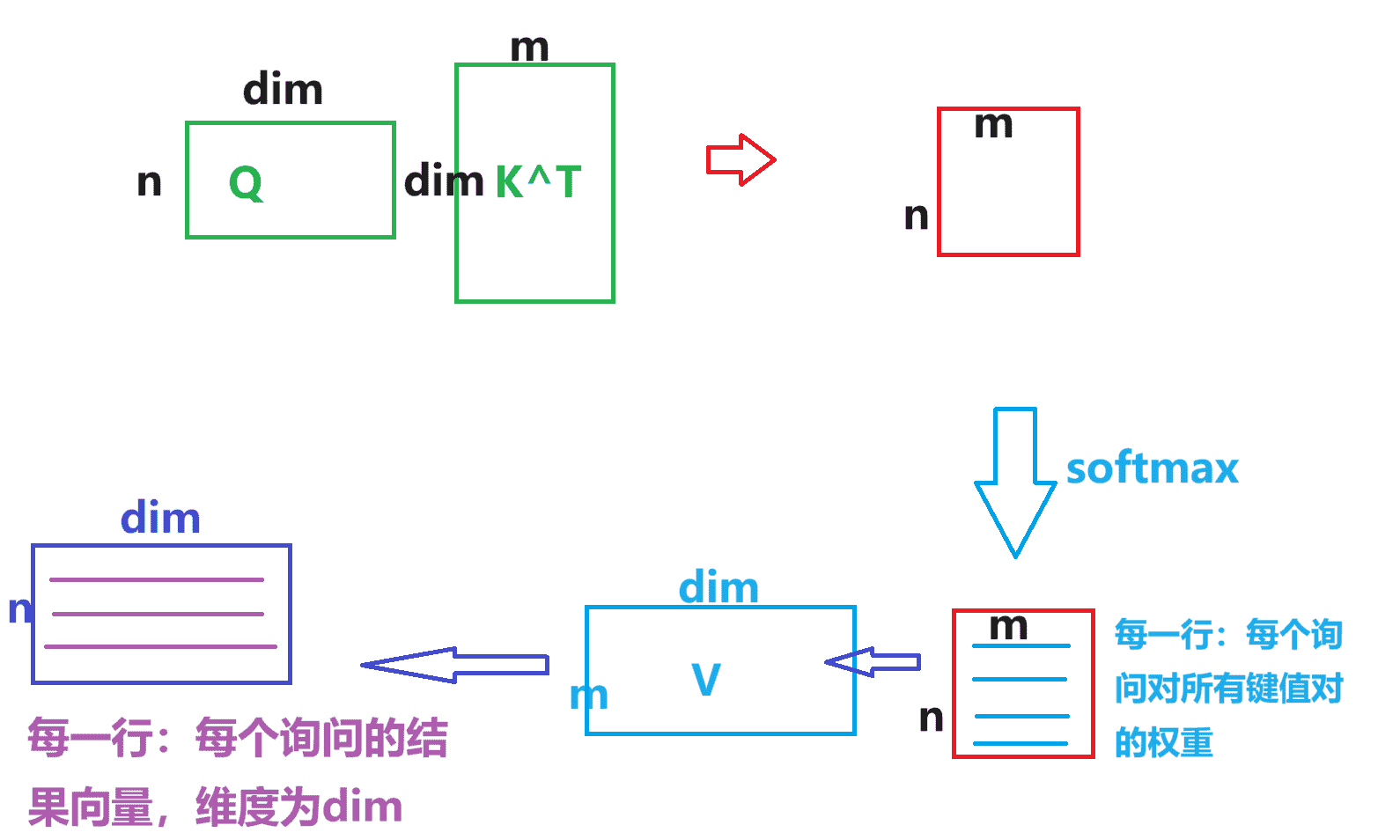
Transformer中设定了d m o d e l = 512 d_{model} =512 d m o d e l = 5 1 2 Q , K , V Q,K,V Q , K , V d i m = 512 dim = 512 d i m = 5 1 2
假设Q Q Q ( n , d i m ) (n,dim) ( n , d i m ) K K K V V V ( m , d i m ) (m,dim) ( m , d i m )
因为是自注意力机制 ,所以n = m n=m n = m q , k q,k q , k
图漏了一个scale
点积速度更快、矩阵乘法方便并行
点积之后做一次sacle,避免在维度较大时,点积结果较大,softmax得到一个较大的值,梯度会更小,更难迭代
Mask:有时候需要计算注意力时,可以得到整个序列;而有时做预测时,是只能看到之前的序列,因此需要mask去屏蔽后面的数值(我们并不会动态改变矩阵大小,而只是修改值),保证计算只有有效的数值参与
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 def attention (query, key, value, mask=None , dropout=None ): d_k = query.size(-1 ) scores = torch.matmul(query, key.transpose(-2 , -1 )) / math.sqrt(d_k) if mask is not None : scores = scores.masked_fill(mask == 0 , -1e9 ) attention_weights = F.softmax(scores, dim=-1 ) if dropout is not None : attention_weights = dropout(attention_weights) return torch.matmul(attention_weights, value), attention_weights
测试:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 batch_size = 2 num_heads = 1 seq_len = 3 d_k = 4 query = torch.rand(batch_size, num_heads, seq_len, d_k) key = torch.rand(batch_size, num_heads, seq_len, d_k) value = torch.rand(batch_size, num_heads, seq_len, d_k) mask = torch.ones(batch_size, num_heads, seq_len, seq_len) output, attention_weights = attention(query, key, value, mask) print (attention_weights.shape)print (output.shape)show_heatmaps(attention_weights)
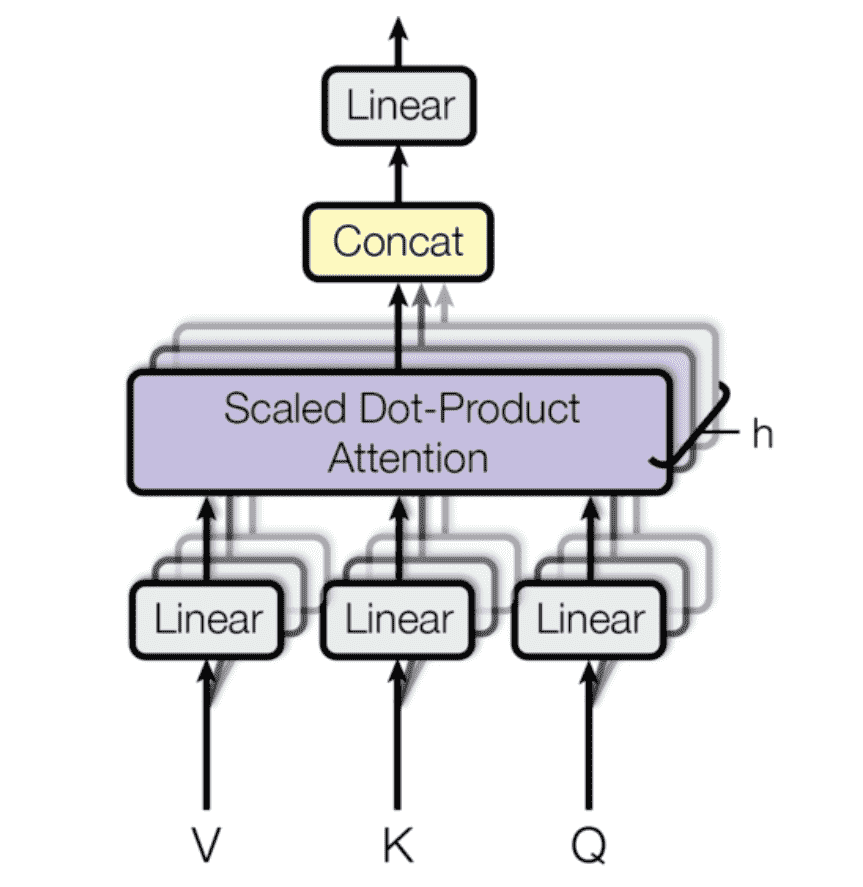
Multi-Head Attention 我们需要引入多头注意力机制,丰富模型对相似度的表达
对于第i i i Q , K , V Q,K,V Q , K , V
求解变化后的注意力,达到丰富相似度的功能
h e a d i = Attention ( Q W i Q , K W i K , V W i V ) head_i = \text{Attention}(QW^Q_i,KW^K_i,VW_i^V)
h e a d i = Attention ( Q W i Q , K W i K , V W i V )
最后我们需要合并所有的h e a d i head_i h e a d i
MultiHead ( Q , K , V ) = Concat ( h e a d 1 , . . . , h e a d h ) W O \text{MultiHead}(Q,K,V) = \text{Concat}(head_1, ...,head_h)W^O
MultiHead ( Q , K , V ) = Concat ( h e a d 1 , . . . , h e a d h ) W O
我们将所有的矩阵连接起来,做一次输出的全连接层或矩阵乘法,重新投影成( n , d m o d e l ) (n,d_{model}) ( n , d m o d e l )
为了保证维度正确,每个h e a d i head_i h e a d i h h h d k = d m o d e l h d_k = \frac{d_{model}}{h} d k = h d m o d e l
Transformer中使用了h = 8 h=8 h = 8 d k = 512 / 8 = 64 d_k=512/8=64 d k = 5 1 2 / 8 = 6 4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 def clones (module, n ): return nn.ModuleList([copy.deepcopy(module) for _ in range (n)]) class MultiHeadedAttention (nn.Module): def __init__ (self, h, d_model, dropout=0.1 ): super (MultiHeadedAttention, self ).__init__() assert d_model % h == 0 self .h, self .d_k = h, d_model//h self .dropout = nn.Dropout(dropout) self .attn = None self .linears = clones(nn.Linear(d_model, d_model), 4 ) def forward (self, query, key, value, mask=None ): if mask is not None : mask = mask.unsqueeze(1 ) batch_size = query.size(0 ) query, key, value = [ linear(x).view(batch_size, -1 , self .h, self .d_k).transpose(1 , 2 ) for linear, x in zip (self .linears, (query, key, value)) ] x, self .attn = attention(query, key, value, mask=mask, dropout=self .dropout) x = x.transpose(1 , 2 ).contiguous().view(batch_size, -1 , self .d_k*self .h) return self .linears[-1 ](x)
测试:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 batch_size = 2 seq_len = 5 d_model = 16 h = 4 query = torch.rand(batch_size, seq_len, d_model) key = torch.rand(batch_size, seq_len, d_model) value = torch.rand(batch_size, seq_len, d_model) mask = torch.ones(batch_size, num_heads, seq_len) mask[:, -1 ] = 0 mha = MultiHeadedAttention(h, d_model) output = mha(query, key, value, mask=mask) print ("Output shape:" , output.shape) assert output.shape == (batch_size, seq_len, d_model), "Output shape mismatch!" print ("Test passed with mask!" ) ''' checking torch.Size([2, 4, 5, 5]) torch.Size([2, 1, 1, 5]) Output shape: torch.Size([2, 5, 16]) Test passed with mask! '''
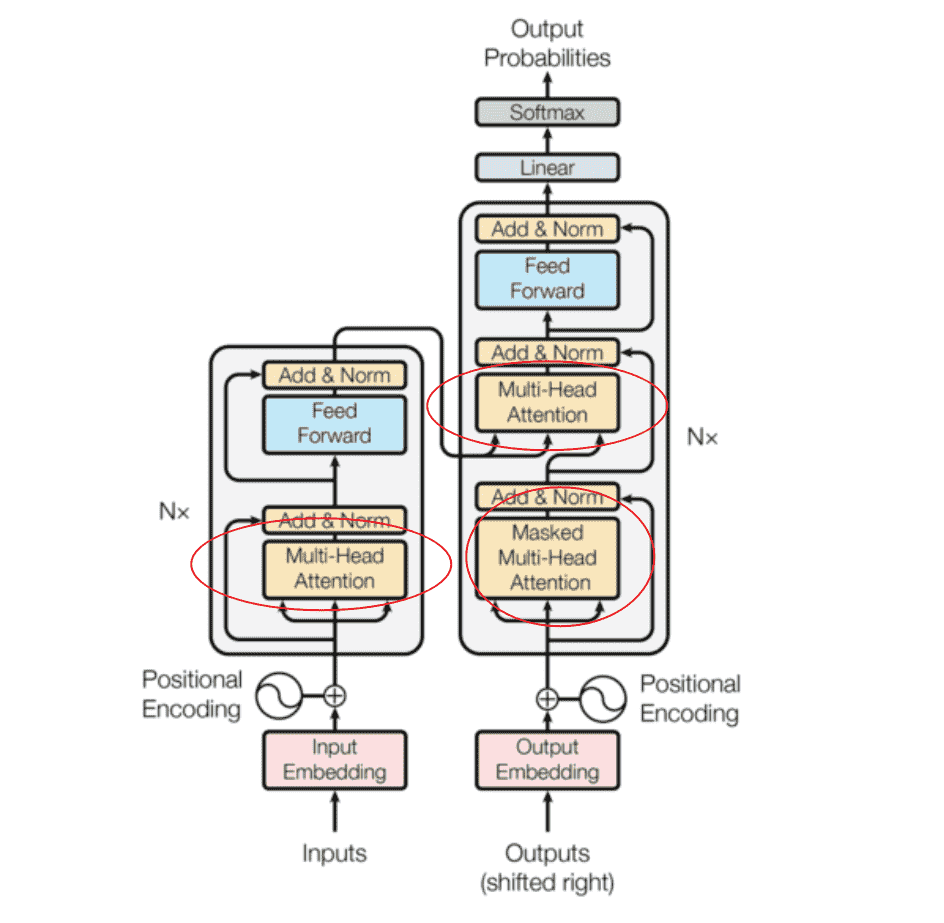
回到Transformer,我们一共使用了三次多头注意力机制:
我们需要搞清楚三次分别读取了什么,实现了什么,输出了什么
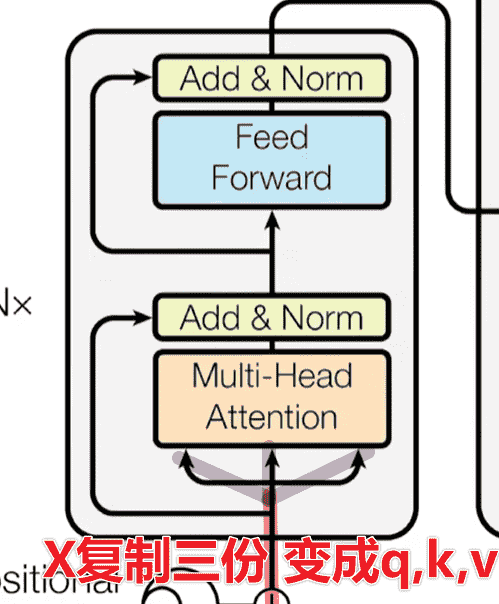
Encoder层的MHA
Key、Value和Query都来同一个地方,这里都是来自Encoder中前一层的输出
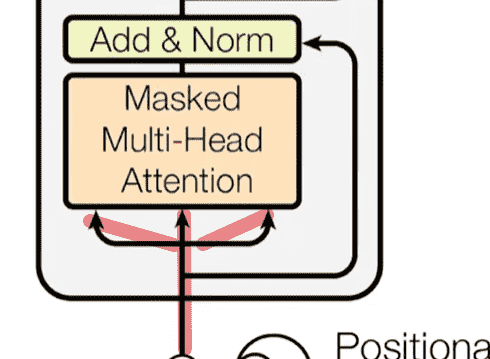
Decoder层的masked-MHA
一样是复制三份
只不过输入的来源不只是源文本,而是添加了之前的预测文本
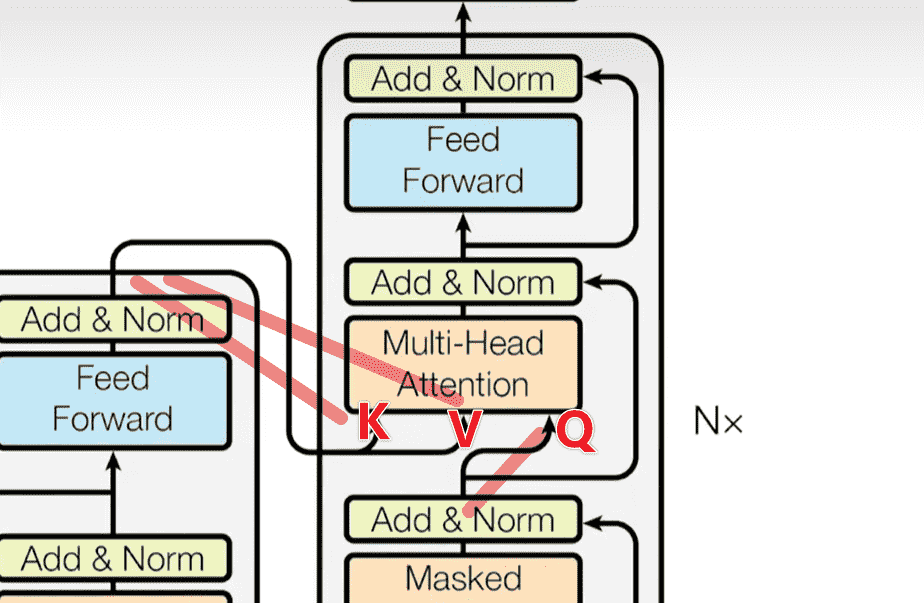
Encoder-Decoder的MHA
Decoder先前的解码器的输出作为Q
Encoder的输出复制两遍,作为K和V
相当于Decoder每次根据当前的输出文本,从给定的源文本的上下文中,挑选更加感兴趣的内容进行加权
Position-wise Feed-Forward Networks encoder和decoder每个块的最后部分的输出,都有一个FFN(前馈神经网络)
多头注意力机制是线性的,因此我们需要引入一点非线性,能够捕捉更复杂的模式和特征
F F N ( x ) = ReLU ( x W 1 + b ) W 2 + b FFN(x) = \text{ReLU}(xW_1+b)W_2+b
F F N ( x ) = ReLU ( x W 1 + b ) W 2 + b
统一设计为单隐藏层的神经网络,输入输出维度均为d m o d e l = 512 d_{model} = 512 d m o d e l = 5 1 2
隐藏层维度d f f = 2048 d_{ff}=2048 d f f = 2 0 4 8
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class PositionwiseFeedForward (nn.Module): def __init__ (self, d_model, d_ff, dropout=0.1 ): super (PositionwiseFeedForward, self ).__init__() self .ffn = nn.Sequential( nn.Linear(d_model, d_ff), nn.ReLU(), nn.Dropout(dropout), nn.Linear(d_ff, d_model) ) def forward (self, x ): return self .ffn(x) temp = PositionwiseFeedForward(512 , 2048 ) x = torch.rand(5 ,1000 , 512 ) x = temp(x) print (x.shape)
Residual Connection&LayerNorm 现在就剩最后一层Add&Norm了
LayerNorm 非常常见的操作,为了保证数值稳定性,加速训练收敛速度
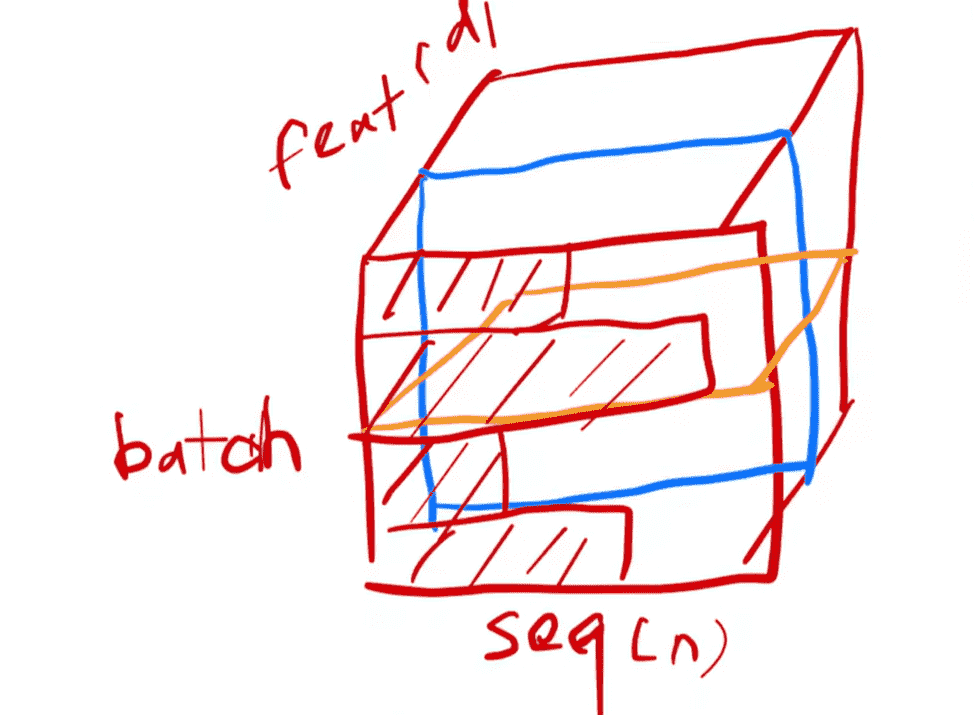
Batch Norm:对于每个Batch中的数据的每一维进行操作
Layer Norm:对于每个样本的所有维度操作
为什么选择Layer而不是Batch?
对于一个Batch来说,数据中会存在seq长度参差不齐的情况,我们想对每一个维度计算均值与方差非常麻烦(我们不能拿填充token参与计算,因此每一维的实际token都不一致)
对于一个数据来说,我们却可以保证维度的数量都是d m o d e l d_{model} d m o d e l
对于单个数据x x x i i i x i x_i x i
LayerNorm ( x ) = a ( x − μ ) σ + ϵ + b \text{LayerNorm}(x) = \frac{a(x-\mu)}{\sigma + \epsilon} + b
LayerNorm ( x ) = σ + ϵ a ( x − μ ) + b
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class LayerNorm (nn.Module): def __init__ (self, dim, eps=1e-6 ): super (LayerNorm, self ).__init__() self .a = nn.Parameter(torch.ones(dim)) self .b = nn.Parameter(torch.zeros(dim)) self .eps = eps def forward (self, x ): mean = x.mean(dim=-1 , keepdim=True ) std = x.std(dim=-1 , keepdim=True ) return self .a * (x - mean) / (std + self .eps) + self .b
测试:
1 2 3 4 5 6 7 8 9 10 11 d_model = 512 layer_norm = LayerNorm(d_model) batch_size = 2 seq_len = 10 output = layer_norm( torch.randn(batch_size, seq_len, d_model) ) print ("Input shape:" , x.shape)print ("Output shape:" , output.shape)''' Input shape: torch.Size([2, 10, 512]) Output shape: torch.Size([2, 10, 512]) '''
Residual Connection 在ResNet中曾经学习过残差连接的概念
我们假设当前的子层为sublayer()
那么为了累加残差,该层的结果则为:x+sublayer(x)
通常还会引入dropout
整合一下,我们可以得到一个残差归一化连接代码:
1 2 3 4 5 6 7 8 9 class SublayerConnection (nn.Module): def __init__ (self, dim, dropout ): super (SublayerConnection, self ).__init__() self .norm = LayerNorm(dim) self .dropout = nn.Dropout(dropout) def forward (self, x, sublayer ): return x + self .dropout(sublayer( self .norm(x) ))
Encoder 开始搭建Encoder层
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class EncoderLayer (nn.Module): def __init__ (self, d_model, self_attention, feed_forward, dropout ): super (EncoderLayer, self ).__init__() self .self_attention = self_attention self .feed_forward = feed_forward self .sublayer = clones( SublayerConnection(d_model, dropout), 2 ) self .d_model = d_model def forward (self, x, mask ): x = self .sublayer[0 ](x, lambda x: self .self_attention(x,x,x,mask) ) return self .sublayer[-1 ](x, self .feed_forward)
Transformer中,EncoderLayer重复总共N=6次
我们封装一个Encoder类:
1 2 3 4 5 6 7 8 9 10 11 12 class Encoder (nn.Module): def __init__ (self, layer, N ): super (Encoder, self ).__init__() self .layers = clones(layer, N) self .norm = LayerNorm(layer.d_model) def forward (self, x, mask ): for layer in self .layers: x = layer(x, mask) return self .norm(x)
测试一下能不能跑通:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 def test_encoder_layer (): d_model, h, d_ff, dropout = 512 , 8 , 2048 , 0.1 self_attention = MultiHeadedAttention(h, d_model, dropout) feed_forward = PositionwiseFeedForward(d_model, d_ff, dropout) encoder_layer = EncoderLayer(d_model, self_attention, feed_forward, dropout) encoder = Encoder(encoder_layer, 6 ) batch_size, seq_len = 2 , 10 x = torch.randn(batch_size, seq_len, d_model) mask = torch.ones(batch_size, seq_len, seq_len) output = encoder(x, mask) print ("Output shape:" , output.shape) assert output.shape == (batch_size, seq_len, d_model), "Output shape mismatch!" print ("Test passed!" ) test_encoder_layer() ''' Output shape: torch.Size([2, 10, 512]) Test passed! '''
Decoder 没什么太大差别
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class DecoderLayer (nn.Module): def __init__ (self, d_model, self_attn, src_attn, feed_forward, dropout ): super (DecoderLayer, self ).__init__() self .d_model = d_model self .self_attn = self_attn self .src_attn = src_attn self .feed_forward = feed_forward self .sublayer = clones(SublayerConnection(d_model, dropout), 3 ) def forward (self, x, memory, src_mask, tgt_mask ): m = memory x = self .sublayer[0 ](x, lambda x: self .self_attn(x, x, x, tgt_mask)) x = self .sublayer[1 ](x, lambda x: self .src_attn(x, m, m, src_mask)) return self .sublayer[2 ](x, self .feed_forward)
1 2 3 4 5 6 7 8 9 10 class Decoder (nn.Module): def __init__ (self, layer, N ): super (Decoder, self ).__init__() self .layers = clones(layer, N) self .norm = LayerNorm(layer.d_model) def forward (self, x, memory, src_mask, tgt_mask ): for layer in self .layers: x = layer(x, memory, src_mask, tgt_mask) return self .norm(x)
Generator 每次得到decoder的输出
我们需要过一遍全连接层,通过softmax进行token的预测
进行输出
1 2 3 4 5 6 7 8 9 class Generator (nn.Module): def __init__ (self, d_model, vocab ): super (Generator, self ).__init__() self .proj = nn.Linear(d_model, vocab) def forward (self, x ): return F.log_softmax(self .proj(x), dim=-1 )
Encoder-Decoder 我们需要合并一下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class EncoderDecoder (nn.Module): def __init__ (self, encoder, decoder, src_embed, tgt_embed, generator ): super (EncoderDecoder, self ).__init__() self .encoder = encoder self .decoder = decoder self .src_embed = src_embed self .tgt_embed = tgt_embed self .generator = generator def encode (self, src, src_mask ): return self .encoder(self .src_embed(src), src_mask) def decode (self, memory, src_mask, tgt, tgt_mask ): return self .decoder(self .tgt_embed(tgt), memory, src_mask, tgt_mask) def forward (self, src, tgt, src_mask, tgt_mask ): return self .decode(self .encode(src, src_mask), src_mask, tgt, tgt_mask)
然后按顺序把每个模块的深拷贝弄进去就行了
后面代码基本直接copy了(没什么太大难度了
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 def make_model (src_vocab, tgt_vocab, N=6 , d_model=512 , d_ff=2048 , h=8 , dropout=0.1 ): c = copy.deepcopy attn = MultiHeadedAttention(h, d_model) ff = PositionwiseFeedForward(d_model, d_ff, dropout) position = PositionalEncoding(d_model, dropout) model = EncoderDecoder( Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N), Decoder(DecoderLayer(d_model, c(attn), c(attn), c(ff), dropout), N), nn.Sequential(Embeddings(d_model, src_vocab), c(position)), nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)), Generator(d_model, tgt_vocab)) for p in model.parameters(): if p.dim() > 1 : nn.init.xavier_uniform(p) return model