[TOC]
Intro
存在的问题:
-
基于分类器的黑盒方法虽然准确,但无法提供解释性。
-
现有生成评分理由的方法(如AERA框架(2305.12962 Distilling ChatGPT for Explainable Automated Student Answer Assessment)存在以下问题:
- 评分准确性不如分类器方法。
- 生成的评分理由可能不忠实于学生答案或评分标准。
paper贡献
- 提出一种新框架,通过模仿人类评分过程生成更忠实的评分理由,同时匹配或超越分类器方法的评分性能。
paper方法
-
模仿人类评分过程
- 使用大语言模型(LLM)生成“思维树”(Thought Tree),将评分任务分解为中间决策步骤。
- 每条树路径代表一个评分决策序列,最终汇总为评分理由。
-
合成数据生成
- 从思维树路径中提取合成评分理由和偏好数据。
- 通过两阶段训练校准LLM:
- 监督微调(SFT):使用合成的评分理由数据。
- 偏好优化(DPO):使用合成的偏好数据,提升评分理由的准确性和忠实性。
paper贡献
- 提出通过思维树生成更忠实的评分理由的方法。
- 开发基于思维树路径正确性的合成偏好数据生成技术。
- 实验表明,框架在QWK分数上比现有方法提升38%,同时生成更高质量的评分理由。
Framework
Problem Set Up
$$ D = \left \{ (x_i, y_i)\right \} $$表示学生$i$对某道题目的答案与得分
对于一道题目,可以划分出$M$个关键得分点$K = \left {k_j\right }$
$$ v(x_i, K) $$该向量的第$j$维度若为1,则表示$x_i$成功回答了$k_j$,否则没有成功回答
$$ y_i = f_r(v(x_i,K)) $$
独热向量 (One-hot Vector):用于表示一个样本只属于一个类别的情况。例如,如果一个动物只能是“- 猫”或“狗”中的一种,那么“猫”可能表示为
[1, 0],“狗”表示为[0, 1]。向量中只有一个 1。多热向量 (Multi-hot Vector):用于表示一个样本可以同时属于多个类别的情况。例如,一个人既是“学生”又是“运动员”,那么可能表示为
[1, 1, 0](假设第一个位置是学生,第二个是运动员)。向量中可以有多个 1
省流:问题的关键在如何判断$x_i$正确回答了$k_j$,记为$1_{x_i}(k_j)$,是一个二分类任务
Stage 1: Imitate Human Assessment Process via Thought Trees
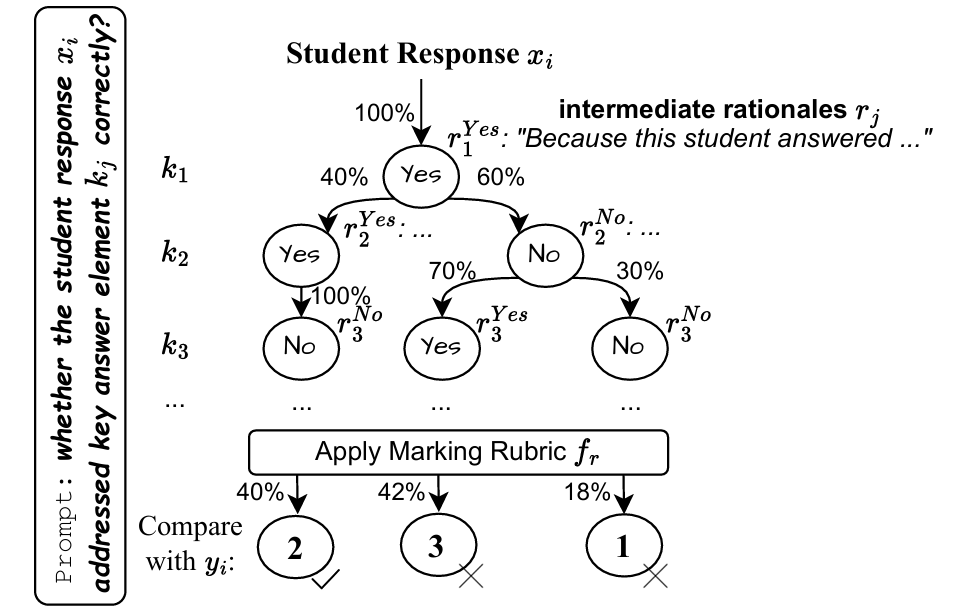
$z_j^{(t)}$ 表示第 $t$ 次采样的决策
我们将这些判定结果汇总,得到如下的平均决策概率:
$$ P(z_j^{\text{Yes}}) = \frac{|\{t : z_j^{(t)} = 1\}|}{n},\quad P(z_j^{\text{No}}) = \frac{|\{t : z_j^{(t)} = 0\}|}{n} $$为了后续聚合,我们为每个关键要素生成简洁的解释性理由 $r_j$,例如:
$$ r_j = \text{LLM}_\theta(x_i, k_j, z_j) $$一旦所有关键要素评估完成,我们便能根据每一组决策 $\mathbf{Z}$ 构造路径。假设总共 $d$ 条路径(最多 $2^{M-1}$ 条),每条路径表示一种判定组合:
$$ \text{path}_l = \hat{\mathbf{v}}(\mathbf{Z}),\quad l=1,2,...,d $$其中,$\hat{\mathbf{v}}$ 是对向量 $\mathbf{v}$ 的估计,表示关键要素是否被覆盖;$\mathbf{Z}$ 是判定集合(由上面的判定概率组成)。路径的概率等于该路径上每个判定概率的乘积:
$$ P(\text{path}_l) = \prod_{j=1}^{M} P(z_j) $$我们利用打分函数 $f_r$(例如程序化的rubric规则)对每条路径打分,获得预测得分:
$$ \hat{y}_{\text{path}_l} = f_r(\text{path}_l) $$省流:蒙特卡洛树,从中抽取所有路径,计算概率和对应的分数,选择概率最高的
最后,选取概率最高的路径作为最终思维树输出结果:
$$ \hat{y}_{\text{tree}} = \hat{y}_{\text{path}_{l^*}} \quad l^* = \arg\max_l P(\text{path}_l) $$“在实际操作中,我们使用LLM动态地将rubric文本转换为可执行Python代码,该代码以关键要素评估决策为输入,输出最终分数。”
人话:LLM会将打分标准生成Python代码,直接传入关键要素的多热向量就可以直接算分