[TOC]
https://www.bilibili.com/video/BV1sd4y167NS
State Value
return 用来衡量不同的trajectory的好坏
首先有如下定义
$$ S_t \overset{A_t}{\rightarrow}R_{t+1}, S_{t+1} $$- $t$表示时间步
- 从状态$S_t$出发,采取$A_t$,转移到$S_{t+1}$,获得了$R_{t+1}$的奖励
$S,A,R$这里表示的是一个随机变量
因此上述内容服从以下概率分布:
- $S_t \to A_t$ :$\pi(A_t| S_t)$
- $S_t, A_t \to R_{t+1}$:$p(R_{t+1}| S_t,A_t)$
- $S_t, A_t \to S_{t+1}$:$p(S_{t+1}| S_t,A_t)$
推广到多步骤之后:
$$ S_t \overset{A_t}{\rightarrow}R_{t+1}, S_{t+1} \overset{A_{t+1}}{\rightarrow}R_{t+2}, S_{t+2}\overset{A_{t+2}}{\rightarrow}R_{t+3} ... $$则可以定义这个trajectory的reward是:
$$ G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ... $$$G_t$也表示一个随机变量
我们定义所有从$t$出发的trajectory的期望$G_t$,即为state-value functionorstate value
return 针对单个、单次的尝试(确定性的)
state value是一种平均情况
Bellman Equation
递推形式
描述不同state的state value之间的关系
对于单个trajectory:
$$ \begin{split} G_t &= R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ...\\ &= R_{t+1} + \gamma \left( R_{t+2} + \gamma^2 R_{t+3} + ...\right)\\ &= R_{t+1} + \gamma G_{t+1} \end{split} $$非常动态规划(或者叫递推)的一个步骤
因此可以推广到期望的情况(事实上可以直接写)
$$ \begin{split} v_\pi(s) &= \mathbb{E}(G_t| S_t = s) \\ &= \mathbb{E}(R_{t+1} + \gamma G_{t+1}| S_t = s) \\ &= \mathbb{E}(R_{t+1}| S_t = s) + \gamma \mathbb{E}(G_{t+1}| S_t = s) \end{split} $$我们考虑去代换两个期望符号
对于第一个期望,其意义是:从$s$出发,得到奖励的均值
$$ \begin{split} \mathbb{E}(R_{t+1}| S_t = s) &= \sum_{a} \pi(a|s) \mathbb{E}(R_{t+1}| S_t=s,A_t = a) \\ &=\sum_a \pi(a|s) \sum_r p(r|s,a) r \end{split} $$始终注意:$R_{t+1}$代表是一个随机变量
对于第二个期望,其意义是:从下一个时刻$t+1$出发可以得到的期望奖励
$$ \begin{split} \mathbb{E}(G_{t+1}| S_t = s) &= \sum_{s'} \mathbb{E}(G_{t+1}| S_{t+1} = s') p(s'| s) \\ &=\sum_{s'} \mathbb{E}(G_{t+1}| S_{t+1} = s') \sum_{a}\pi(a| s)p(s'| s,a)\\ &=\sum_{s'} v_{\pi}(s') \sum_{a}\pi(a| s)p(s'| s,a) \end{split} $$综上,整理一下原式子:
$$ \begin{split} v_\pi(s) &= \mathbb{E}(R_{t+1}| S_t = s) + \gamma \mathbb{E}(G_{t+1}| S_t = s) \\\\ &= \sum_a \pi(a|s) \sum_r p(r|s,a) r+\gamma\sum_{s'} v_{\pi}(s') \sum_{a}\pi(a| s)p(s'| s,a)\\ &= \sum_a \pi(a| s) \left[ \sum_r p(r| s,a)r + \gamma \sum_{s'}p(s'| s,a){\color{Red} v_\pi(s')} \right], \forall s\in S \end{split} $$这里的$S$是state space
这样我们就得到了贝尔曼公式,由两个部分组成:
- immediate reward
- future reward
通常我们会使用给定的$\pi(a|s)$,因此这个过程可以被视作Policy Evaluation
$p(r|s,a),p(s’|s,a)$在这里是已知的
但其实不知道也有办法去求解
向量形式
我们先把贝尔曼公式进行重写,用一些其他符号进行替代:
$$ v_\pi(s) = r_\pi(s) + \gamma \sum_{s'} p_\pi(s'|s)v_\pi(s') $$表示基于策略$\pi$获取的当前奖励,以及之后的期望奖励
我们令所有的状态依次编号为:$1\to n$
对于状态$s_i$,其state value表示为:
$$ v_\pi(s_i) = r_\pi(s_i) + \gamma \sum_{s_j} p_\pi(s_j|s_i)v_\pi(s_j) $$把所有$s_i$写在一起,自然就是向量形式:
$$ v_\pi = r_\pi + \gamma P_\pi v_\pi $$- $v_\pi = \left[ v_\pi(s_1), …,v_\pi(s_n) \right ]^T \in \mathbb{R}^n$
- $r_\pi = \left[ r_\pi(s_1), …,r_\pi(s_n) \right ]^T \in \mathbb{R}^n$
并且有:
$$ P_\pi \in \mathbb{R}^{n\times n}, \text{where} \space [P_\pi]_{i,j} = p_\pi(s_j|s_i) $$理解一下图:
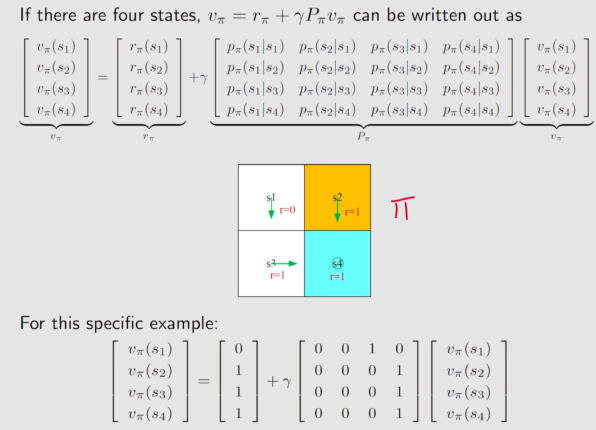
Solve State Values
我们需要通过state value衡量当前的policy的表现
因此需要进行求解
Method 1 · closed-form solution
$$ v_\pi = r_\pi + \gamma P_\pi v_\pi\\ (I-\gamma P_\pi)v_\pi = r_\pi\\ v_\pi = (I-\gamma P_\pi)^{-1}r_\pi $$但是由于需要求逆矩阵,计算量过高,这个方法一般不会使用
Method 2 · iterative solution
$$ v_{\pi, k+1} = r_\pi + \gamma P_\pi v_{\pi,k}\\ $$我们不断迭代这个等式,可以使得最后有:
$$ v_{\pi,k} \to v_\pi = (I-\gamma P_\pi)^{-1}r_\pi, k \to \infty $$Action Value
- 与state value相比,不止固定了当前的状态,action value同时固定了当前执行的动作
- action value意义很大,有时候我们倾向于采取能带来最大value的action
定义如下:
$$ q_\pi(s,a) = \mathbb{E}\left[G_t|S_t=s,A_t=a\right] $$同时有:
$$ \underbrace{\mathbb{E}[G_t \mid S_t = s]}_{v_{\pi}(s)} = \sum_{a} \underbrace{\mathbb{E}[G_t \mid S_t = s, A_t = a]}_{q_{\pi}(s,a)} \pi(a \mid s) $$因此:
$$ {\color{Red} v_\pi(s)} = \sum_a \pi(a|s){\color{Red} q_\pi(s,a)}\\ q_\pi(s,a) = \sum_r p(r| s,a)r + \gamma \sum_{s'}p(s'| s,a){\color{Red} v_\pi(s')} $$- 第一个式子:通过所有action value,求解当前state value
- 第二个式子:通过所有state value,求解当前action value
求解的方式比较多样
- 通过state value
- 通过数据采样进行求解(后文)