强化学习的数学原理 · Chap4 · Value Iteration and Policy Iteration

[TOC]

Value Iteration

基于BOE：

$$ v = f(v) = \max_\pi(r_\pi+\gamma P_\pi v) $$

我们不断做迭代：

$$ v_{k+1} = f(v_k), k=1,2,3,... $$

这个就是value iteration

整个算法可以拆成以下步骤：

$$ \pi_{k+1} = \arg\max_\pi (r_\pi+\gamma P_\pi v_k) $$

基于上一步的state value，找出当前最优的策略

$$ v_{k+1} = r_{\pi_{k+1}} + \gamma P_{\pi_{k+1}}v_k $$

基于该策略，更新所有的state value

理论上$v_k$不能被称为state value

由于所有的state都是在优化过程，因此不能保证所有state都符合贝尔曼公式

因此只是一个临时状态

从代码实现的角度：

Step0：若$\left| v_k - v_{k-1}\right | > \text{eps}$
- 否则结束，说明收敛
- 对所有的state，计算出所有的$q(s,a)$
- 得到$a^*_k(s,a) = \arg \max_a q_k(s,a)$
Step1：

$$ \pi_{k+1}(a|s) = \begin{cases} 1 & \text{ if } a=a^*_k(s) \\ 0 & \text{ if } a\neq a^*_k(s) \end{cases} $$

这是一个贪心的策略

$$ v_{k+1}(s) = \max_a q_k(s,a) $$

Value Iteration从当前的state value出发，决定了下一个Policy

使用新的Policy去更新state value

与之相比，还有一种迭代方式是以Policy作为基础

与Value Iteration不同，我们的出发点是一个初始策略$\pi_0$

进行如下迭代：

$$ v_{\pi_k} = r_{\pi_k} + \gamma P_{\pi_k} v_{\pi_k} $$

这里的求解依赖于一个迭代的过程

因此整个Policy Iteration，内含一个小的迭代

$$ \pi_{k+1} = \arg \max_\pi (r_\pi + \gamma P_\pi v_{\pi_k}) $$

从代码实现的角度

Step1：$v_{\pi_k}$基于策略$\pi_k$不断迭代，直到$v_{\pi_k}$收敛
Step2：基于$v_{\pi_k}$算出所有的$q_{\pi_k}$
- 得到$a^*_k(s,a) = \arg \max_a q_k(s,a)$
- 同样做以下事情：

$$ \pi_{k+1}(a|s) = \begin{cases} 1 & \text{ if } a=a^*_k(s) \\ 0 & \text{ if } a\neq a^*_k(s) \end{cases} $$

策略迭代会出现一个现象：接近终点的策略会先变好

因为一开始都是乱七八糟的，接近终点的策略会更先找到方向

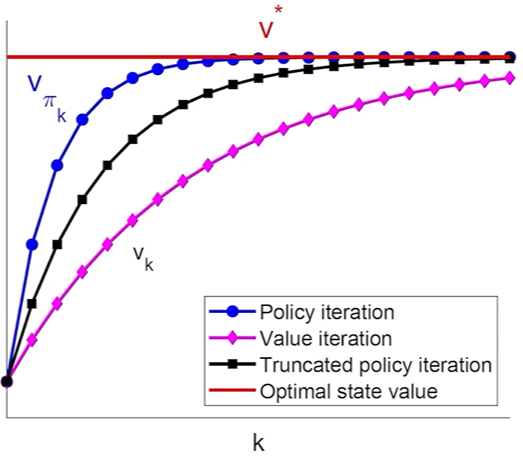
对两个算法进行对齐

前面说了：Policy Iteration是一个大的迭代包含一个小的迭代过程

而value iteration的第一次迭代得到的$v_1$，事实上就是Policy iteration小迭代中的第一个中间量

我们显然不会在这里进行无穷次的迭代

所以这个迭代次数就可以一般化成Truncated Policy Iteration（截断策略迭代）

当迭代次数为：

所以Truncated Policy Iteration是两个算法的一般化形式