L4. Sequence as input

ML 2022 Spring (ntu.edu.tw)

https://www.bilibili.com/video/BV1VN4y1P7Zj

[TOC]

Sequence

对于Sequence Labeling任务，我们需要对一段文本中的所有单词标注词性。

显然不能单独考虑一个单词，需要结合上下文
- 同一个单词在不同的上下文中会有不同的词性

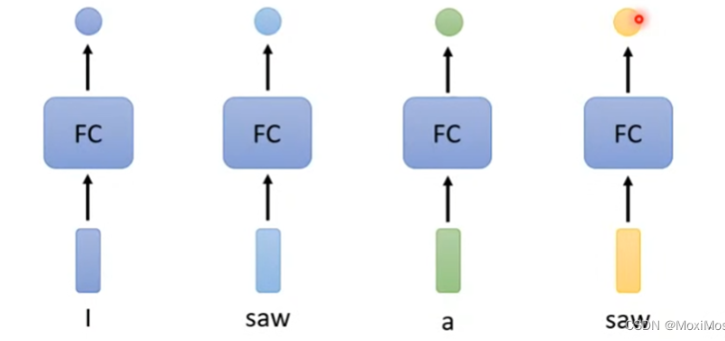
我们考虑定义一个window：
- 每个Fully-Connected需要连接前后若干个单词作为输入

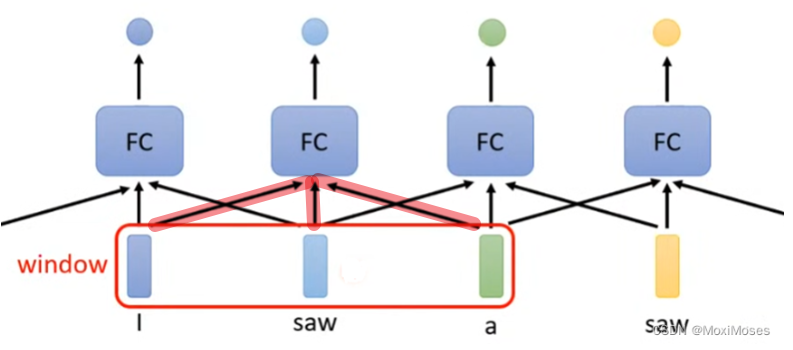
但是我们有时需要考虑整个Sequence去获得信息，我们很难通过扩大Window进行操作，复杂度会非常高

Self-Attention

概述

整个Sequence作为输入
输出向量数量等于输入向量

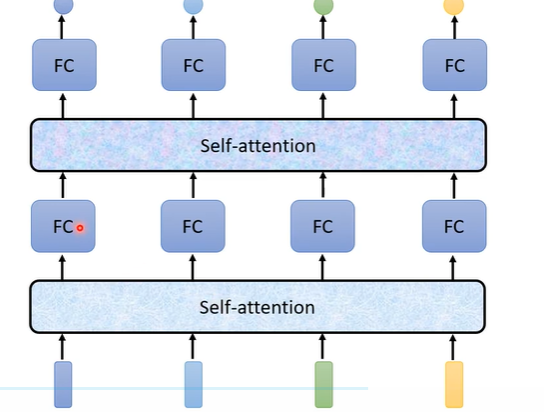
每次完成Self-Attention后，喂入FC进行操作
可以多次叠加

Dot-Product

我们会对多个输入向量之间的相关性感兴趣

Self-Attention常使用Dot-Product求出两个向量之间的相关性

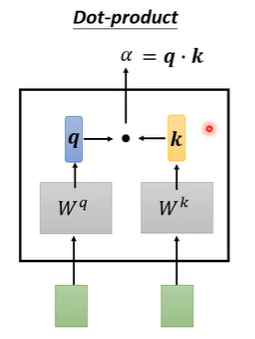
两个输入$\text{query},\text{key}$向量分别乘上$W_q,W_k$，得到向量$q,k$
对向量$q,k$进行点积，得到$\alpha$，同时也被称为attention-score

Forward

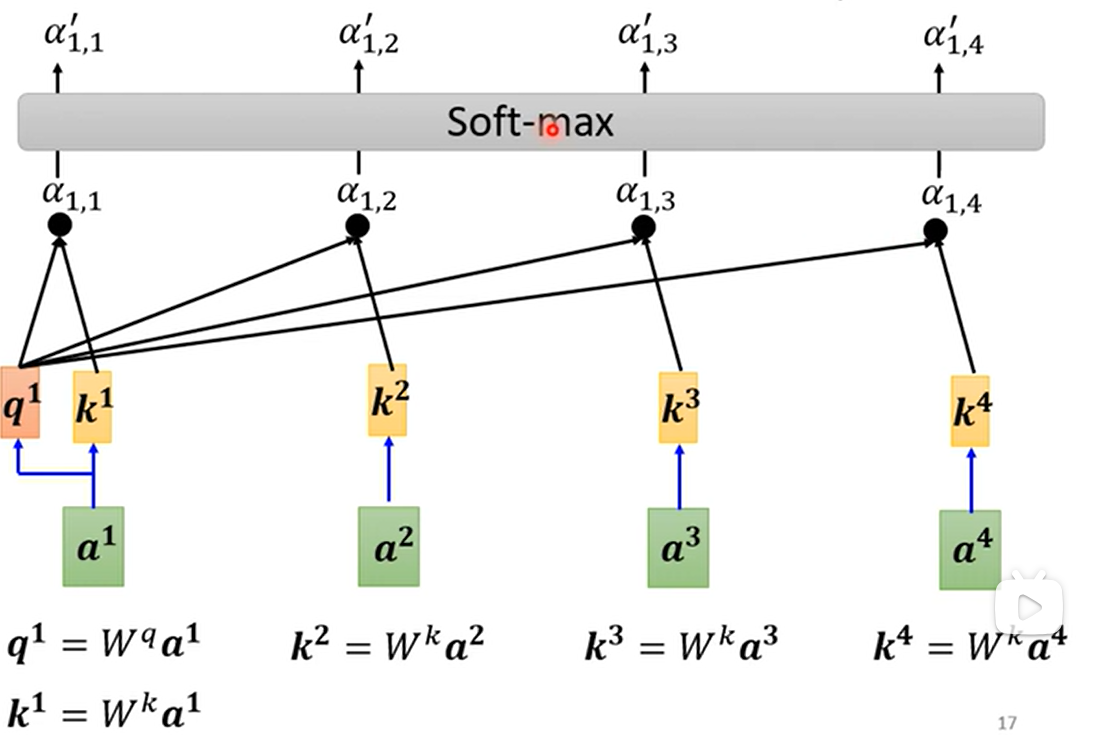
对于其中一个向量$i$，计算出自己作为查询向量的$q_i$值
所有向量都需要计算自己作为被查询向量的$k_j$值
通过Dot-Product，得到$\alpha_{i,j}$，即向量$i$对所有向量$j$的相关性
做一下Softmax，得到$\alpha’_{i,j}$

每个向量都需要通过$W_v$矩阵计算出向量$v$
$v_j$乘上标量$\alpha_{i,j}$，求和
$$ b_i = \sum_{j} \alpha'_{i,j}v_j $$

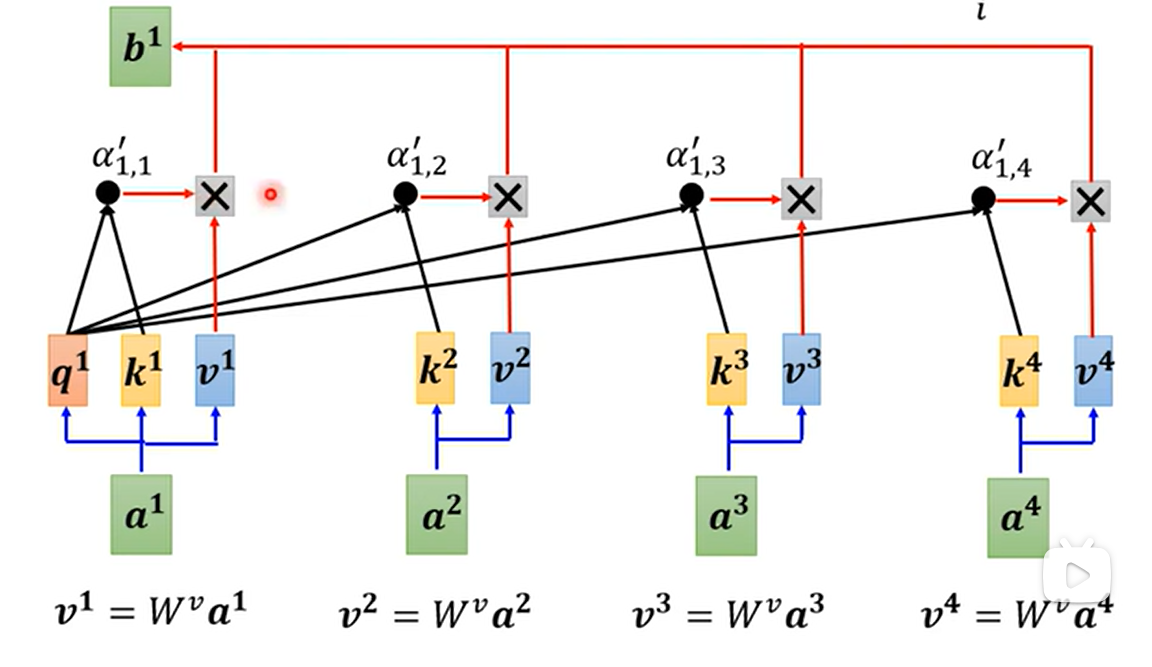
关联性越高的向量，它会$b$占有很大的成分

每个向量$a_i$得到$b_i$的计算过程是并行进行的

Forward（矩阵形式）

$W_q,W_k,W_v$都是通用的，每个向量$a_i$都需要使用，因此很容易就能表示成矩阵形式

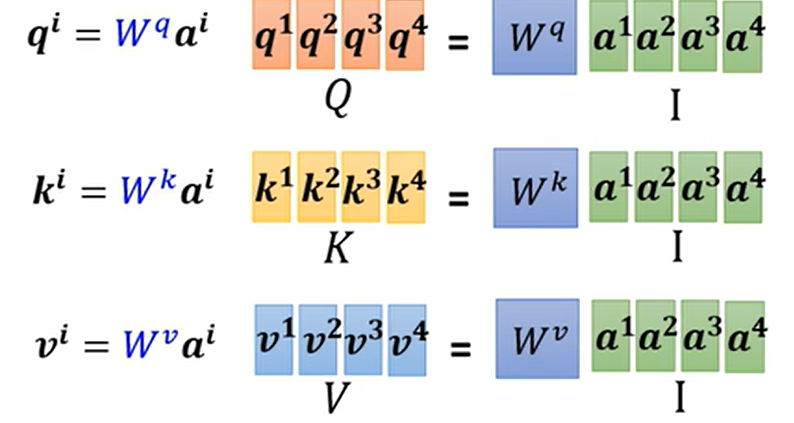
对于$q_1$，我需要让它与所有$k_j$进行点积运算
实质上就是与$k_j^T$进行相乘

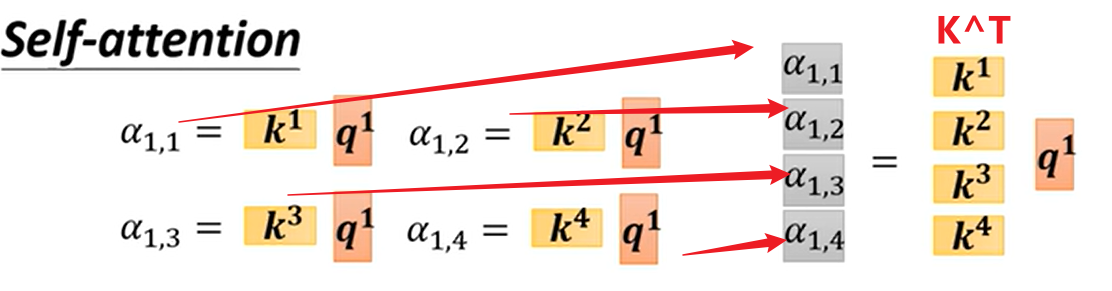
对于其他$q_i$也是同理，计算得到矩阵$A$
通过矩阵$A$，每一列过一遍激活函数（softmax）得到$A'$

计算输出矩阵

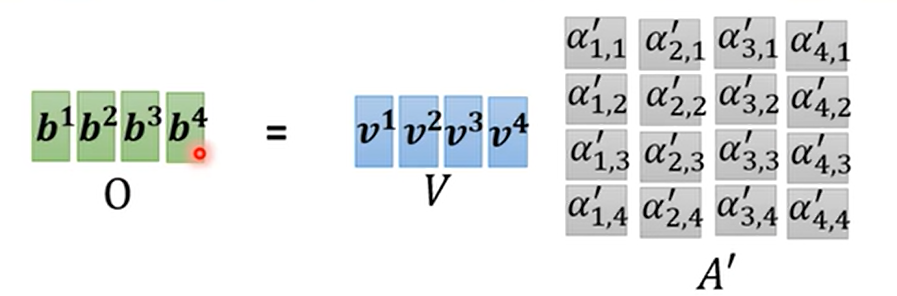
整理一下：

$$ O = VA' = (W_vI)\text{softmax}(A) \\ O =(W_vI)\text{softmax}( K^TQ ) = (W_vI)\text{softmax}( I^TW_k^TW_qI ) \\ $$

$W_q,W_k,W_v$则是我们需要学习的参数矩阵

Multi-head Self-Attention

一般的Self-Attention只会有一种$W_q$得到的一组$q$向量，作为相关性的度量

但是有时候需要丰富多个相关性指标

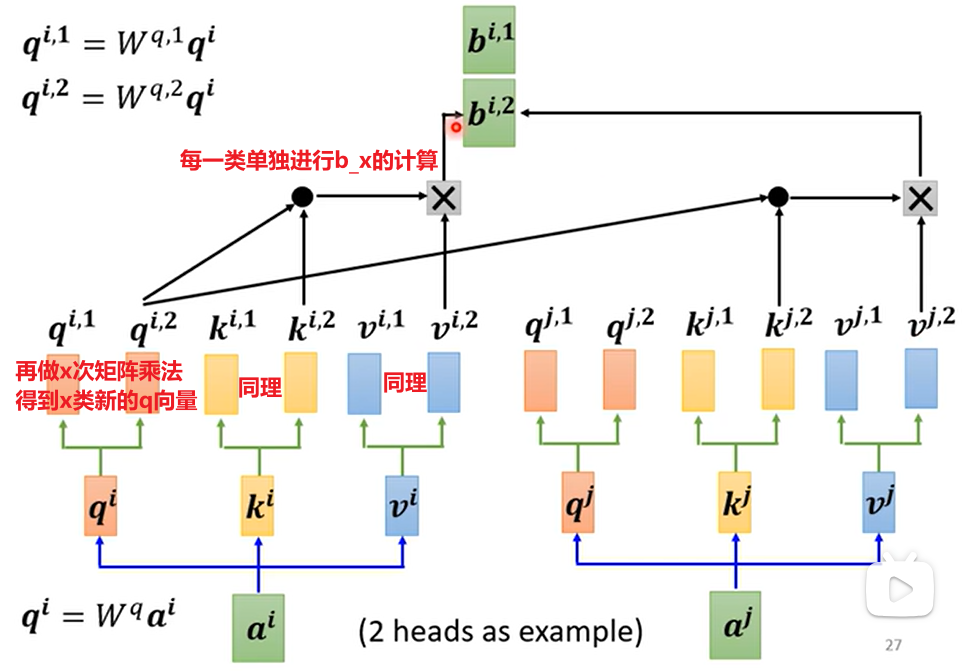
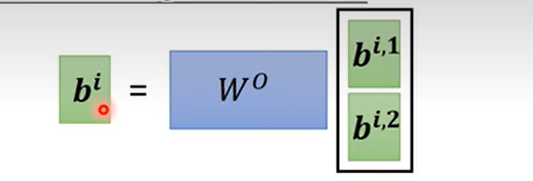
得到的多类$b_i$输出，拼起来乘一个矩阵，得到最后的输出

Position Encoding

对于$a_1, a_2, a_3, a_4$，其对于上文算法来说，并没有距离的概念（交换位置后没什么差别）
但对于实际文本来说，$a_1,a_4$是距离较远的向量，$a_2,a_3$是距离较近的向量
（需要分析一下位置对实际要的输出是有影响，才会考虑引入Position Encoding）
在求解前，每个$a_i$需要加入一个位置向量$e_i$即可

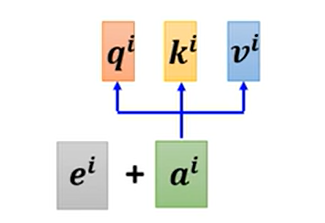
hand-crafted（人为设置）：会使用一些三角函数进行组合
- 方式非常多，暂时没有最好的

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


// 好像自己写过这个东西
__global__ void cu_matrixPositionalEmbedding(float* d_C, float* d_A, int M, int N, int level) {
    int idx = blockIdx.x * blockDim.x + threadIdx.x;
    if (idx < M * N) {
        int row = idx / N;
        int col = idx % N;
        
        int pos = row * N + col;
        d_C[pos] = d_A[idx]; pos += M * N;
        
        float powf2 = 1.0;
        for (int l = 0; l < level; ++l, powf2 *= 2) {
            float val = d_A[idx] * powf2;
            d_C[pos] = sinf(val); d_C[pos + M * N] = cosf(val);
            pos += 2 * M * N;
        }
    }
}

learn from data：直接作为参数进行学习

非文本应用

省流：只要是一个vector set，就可以进行self-attention

Self-attention for Speech
- 声音讯号转换成向量会更加复杂
- 导致整体的矩阵会变得非常大
- 所以需要引入window，考虑一小段话进行识别
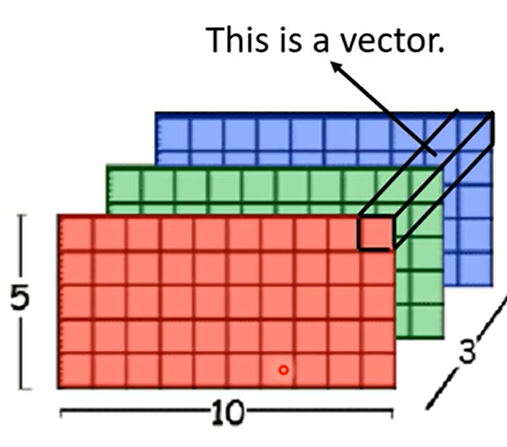
Self-attention for Image
- 每个像素的所有通道值看作一个向量
- 则我们可以得到分辨率数个向量，构成了一个vector set
- 相比CNN来说，可以考虑整个图像的所有像素，而不是一个感受野
  - 自动学习出附近哪些像素是相关的，本质上自动学习了感受野
  - 不需要人为设定感受野大小
  - 认为：Self-Attention经过调整可以做到CNN一样的事情，因此对于function set层面上，CNN被Self-Attention所包含，是有所限制的特例

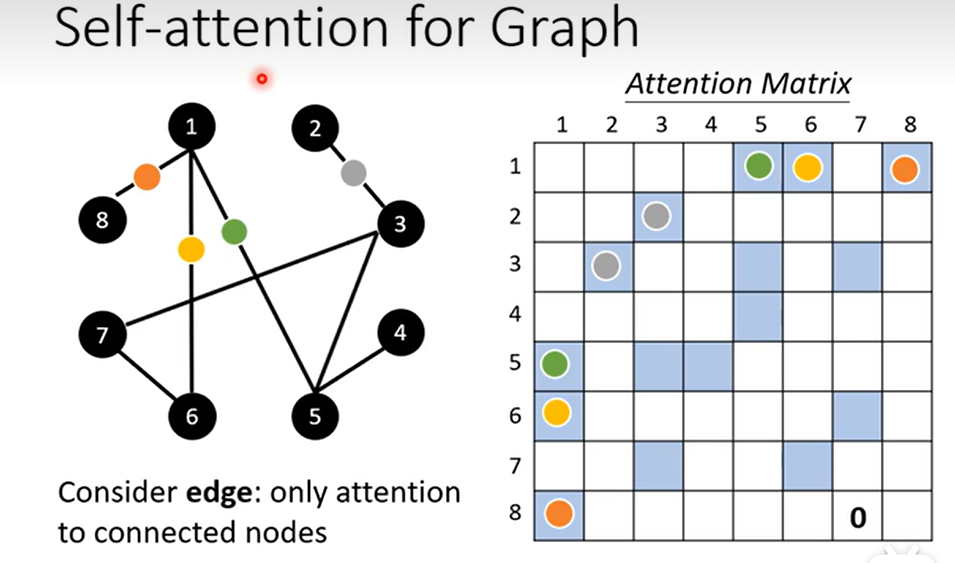
Self-attention for Graph
- 对于有边的结点对，需要计算attention-score
- 没有边可以直接认为无关，设为0
- 改改就是GNN

RNN

似乎被Self-Attention替代了

RNN没法并行
普通的RNN只会考虑左边序列的输出，而Self-Attention考虑整个序列
双向RNN需要大量memory去存储结果，才能做到考虑整个序列