浅谈MinHash

常用于网页、文本去重

前置知识

n-gram

• 通过分词将文本分解为连续的n个单词或字符序列

例如：

1

"This is an example sentence for n-gram extraction."

表示为3-gram：

1
2
3
4
5
6

('This', 'is', 'an')
('is', 'an', 'example')
('an', 'example', 'sentence')
('example', 'sentence', 'for')
('sentence', 'for', 'n-gram')
('for', 'n-gram', 'extraction')

按照此方式可以将一段文本表示成一个n元组序列，每个元组可以考虑到一定的上下文

Jaccard相似度

假设一共有$N$篇文档，每篇文档大小都是$M$，我们想知道两两文档之间的Jaccard值的开销是$O(N^2M)$

对于超大规模的文档，一般来说$M$会占大头，文档的大小都非常恐怖

流程

因此MinHash的目标是将一篇大文档表示为一个较短的signature（假设大小为$\text{numHash}$）

本质上在做数据降维

重要的前提：两个集合非常相似，那么对两个集合使用相同的变化，得到的变化结果也是相似的

例如对于$A,B$两个集合，同时使用函数$\min$，结果$\min(A),\min(B)$大概率也是相同的

基于Hash的方法

假设哈希就用最简单的

1
2

def hash(x, a, b, p):
    return (a*x + b) % p

因为叫MinHash，所以取最小值

1
2

def MinHash(document, hash):
    return min(hash(x) for x in document)

为什么这个公式是对的？

假设有30个小朋友，有的会唱歌、有的会跳舞，有的什么都会

定义：

• A = 会唱歌的集合
• B = 会跳舞的集合
• A和B的并集即为全集

我们从A中挑选身高最高的小朋友，B中也挑选一个最高的小朋友

两个小朋友是同一个小朋友的概率，等价于从全班中挑选一个身高最高的小朋友，他同时属于A和B

我们还可以使用：

• 体重
• 力气
• 成绩

等多种方式（本质上是多种哈希），将所有元素投影到一个方向，完成近似

我们只要使用多个hash函数进行测试，就可以估计出$\text{Jaccard}(A,B)$

实际操作中略微复杂，会更偏向于使用随机打乱的方法

基于随机打乱的方法

将$N$个文档中的所有token抽取出来去重，假设是一个长度为$M$的集合

那么每个文档自然可以表示为一个$M$维的01向量

我们把所有文档写在一起就是一个 $M\times N$的矩阵

例如：上山打老虎和老虎不在家

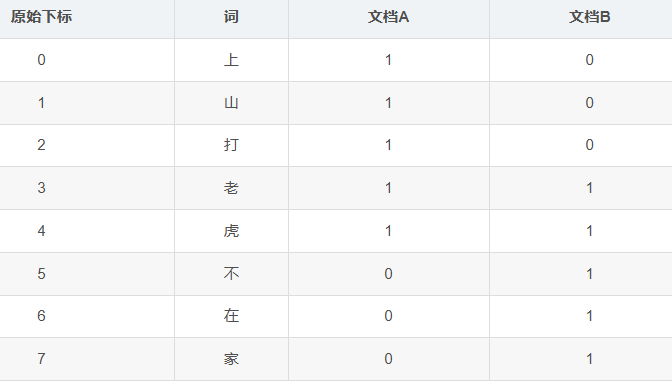
也就是说每个token对应的下标顺序如果不一致，我们表示每个文档的向量也是不一样的

我们进行一次打乱得到：

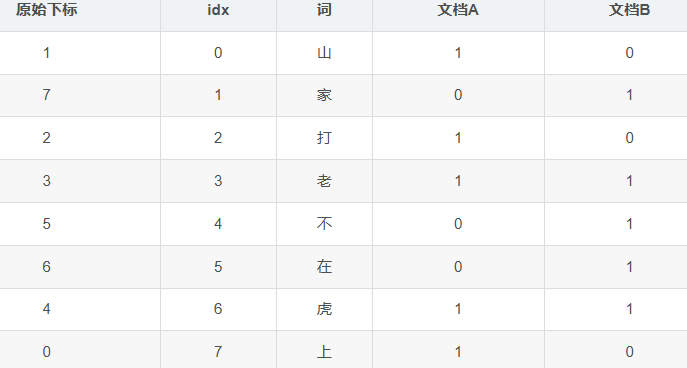
此时我们的Min选择表示向量出现第一个1的idx

例如第一张图：A是0，B是3；第二张图：A是0，B是1

我们进行多次这样的打乱排序

并统计他们相等的次数，除以总次数，就是估计出来的值

在打乱前只执行一次Hash即可，与前文的方法相比，是避免了多次hash计算，最终效果相似