[TOC]
https://www.bilibili.com/video/BV1A9tszhEpp/
微积分
总体依照:3blue1brown 微积分的本质
导数
情景:车随时间变化,采用不同的速度,行驶的距离
因此会建立一个:路程关于时间的函数,假设为:
$$ s(t) = t^2 $$$$ v(x) = \frac{s(x+dt)-s(x)}{dt} = \frac{x^2+(dt)^2+2xdt - x^2}{dt} = dt+2x $$$$ v(x) = 2x $$从几何角度出发:
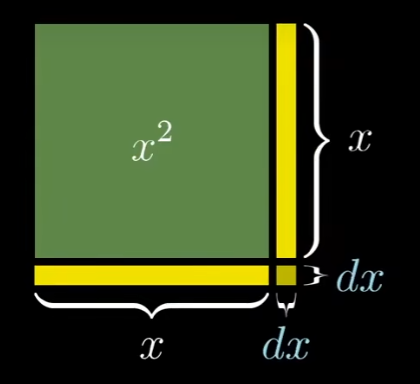
对于一个面积为$x^2$的正方形,两边分别延长$dx$
$$ dA = xdx+xdx+d^2x = 2xdx $$$d^2x$足够小,应该被忽略
$$ \frac{dA}{dx} = 2x $$$$ A_{new} = (x+dx)^n = x^n+nx^{n-1}dx+.... \\ A_{old} = x^n\\ dA = A_{new} - A_{old}=nx^{n-1}dx\\ \frac{dA}{dx} = nx^{n-1} $$链式法则
求导只需要解决三个问题:
- 函数相加
- 函数相乘
- 函数嵌套函数
所有函数都可以被表示为几个基本函数通过上述操作得到的
函数相加
对于函数:
$$ f(x) = \sin(x) + x^2 $$其积分应该为:
$$ df = \sin(x+dx)+(x+dx)^2 - (\sin x + x^2) \\ df = (\sin(x+dx) - \sin x) + ((x+dx)^2-x^2)\\ df = d(\sin x)+ d(x^2) $$函数相乘
同样的我们可以用面积来表示乘积,对于函数:
$$ f(x) = \sin(x)\times x^2 $$我们使用两个函数分别作为矩形的长与宽
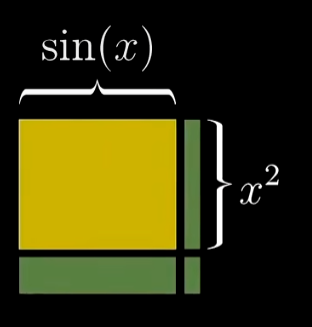
当自变量增加$dx$,则增加的面积可以表示为:
$$ df = \sin x\times d(x^2) + d(\sin(x))x^2 + d(x^2)d(\sin(x)) $$最后一项可以省略
函数复合
链式法则:
$$ \frac{dg(h(x))}{dx} = \frac{dg}{dx} = \frac{dg}{dh}\times\frac{dh}{dx} $$指数函数求导
例如:
$$ M(t) = a^t $$求导:
$$ \frac{dM}{dt} = \frac{a^{t+dt}-a^t}{dt} = a^t\frac{(a^{dt}-1)}{dt} $$此时函数右边这一项只与$dt$有关
$$ \lim_{x\to0^+}\frac{e^x-1}{x} = 1 $$$$ M(t) = a^t = e^{t\ln(a)} $$$$ \frac{dM}{dt} = \frac{dM}{du}\frac{du}{dt} = e^u\ln a = a^t\ln a $$隐函数
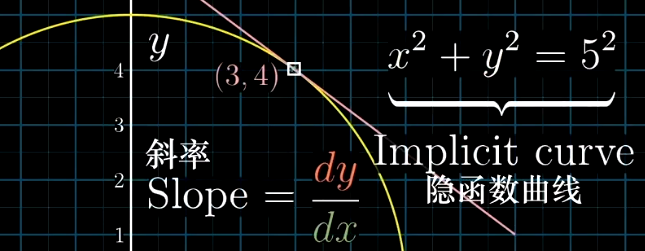
对于某个存在关系的$x,y$,他们都是自变量而非因变量,因此不存在函数上的导数关系
他们在某处的斜率被定义为:
$$ \frac{dy}{dx} $$对于上述圆方程,对这个隐函数的求导:两边同时求导:
$$ 2xdx+2ydy = 0 \\ \frac{dy}{dx} = -\frac{x}{y} $$分析其几何意义:
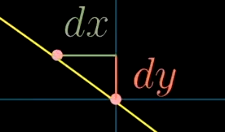
$x,y$分别变换了$dx,dy$,因此$2xdx+2ydy$表示的就是$x^2+y^2$的变化量
而这个变化量为0时,$x,y$仍然在$x^2+y^2=5^2$上
否则就会离开曲线
自然对数函数求导
本质上是对$y=\ln(x)$这条曲线上的某个点求斜率
在这条曲线上的点$(x,y)$,必然满足:
$$ e^y = x $$同样也是一条曲线,我们可以两边求导:
$$ e^ydy = dx\\ \frac{dy}{dx}= \frac{1}{e^y}= \frac{1}{x} $$极限
$$ \frac{df}{dx}(x) = \lim_{h\to 0}\frac{f(x+h)-f(x)}{h} $$对于$\frac{0}{0}$型的函数,在该点是不存在函数值的
但是可能存在极限,通常使用洛必达法则进行求解
从几何意义出发
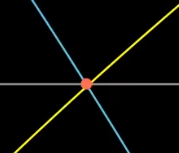
只要把这个点放大足够大,这一处的函数可以被近似为两条直线
$$ \lim_{x\to a}\frac{f(x)}{g(x)} = \frac{\frac{df}{dx}(a)dx}{\frac{dg}{dx}(a)dx} =\frac{\frac{df}{dx}(a)}{\frac{dg}{dx}(a)} $$积分
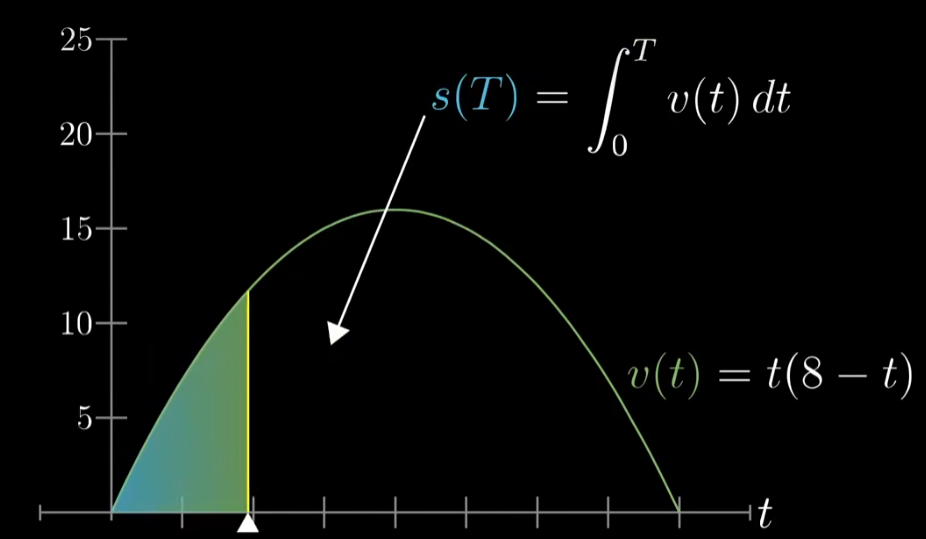
对于速度函数
$$ v(t) = t(8-t) $$$$ s(T) = \int_0^{T}v(t)dt $$这个函数实质上就是距离函数
而距离函数关于时间的导数,正是速度函数
因此:
$$ \int f(x)dx = F(x) + C\\ \frac{dF(x)}{dx} = f(x) $$通常会写成:
$$ \int_a^bf(x)dx = F(b)-F(a) $$泰勒级数
对于三角函数$\cos \theta$,我们可以考虑使用多项式进行拟合
$$ P(x) = c_0 + c_1x + c_2x^2 $$对于$x=0$处,$\cos (0) = 1$
因此$P(0) = c_0 = 1$
$$ \frac{d \cos x}{dx} = -\sin x = 0\\ \frac{dP(x)}{dx} = c_1 + 2c2x = c_1 = 0 $$$$ \frac{d^2 \cos x}{dx^2} = \frac{d(-\sin x)}{dx} = -\cos x = -1\\ \frac{d^2P(x)}{dx^2} = 2c_2 \\ c_2 = -\frac{1}{2} $$$$ \frac{d^nf(x)}{dx^n} = n!c_n\\ $$$$ f(x) = \sum \frac{1}{n!}\frac{d^nf(x)}{dx^n}x^n $$