CS231A:Computer Vision, From 3D Reconstruction to Recognition
[TOC]
L2. Camera Models
pinhole camera(小孔成像 - 摄像机)
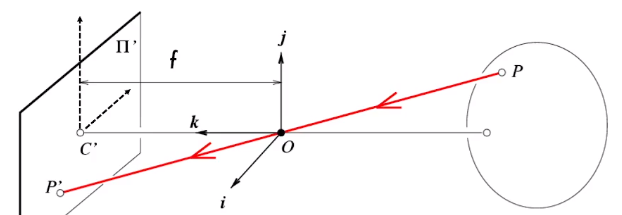
- $f$:定义为相机焦距
物理课的小知识
- 小孔越小,透光越少,但是画面清晰
- 小孔越大,透光越多,但是画面模糊
因此为了全部都要,引入了Lens(透镜)
Lenses and Cameras(透镜和相机)
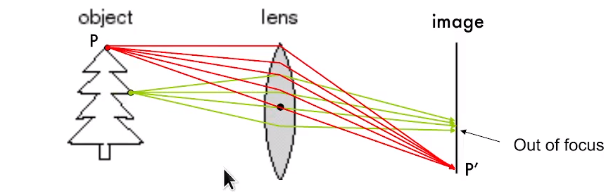
- 除了通过中心的光线,其他光线都会被折射
- 在一定距离,所有入射光线会被折射到图像的一点上
- 少于或多于这段距离,光无法聚焦在一个点上(Out of focus)
景深(Depth of Field)则是指在摄影或者摄像中,一张图像中能够保持清晰度的距离范围。
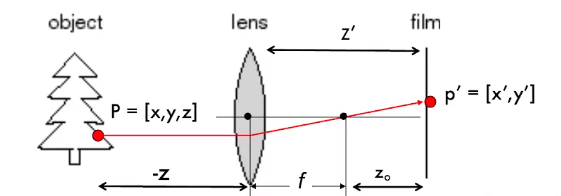
定义参数等效焦距$z’=f + z_0$,$z_0$为像距
$$ x' = \frac{z'}{z}x,y' = \frac{z'}{z}y $$但由于工艺问题,透镜成像的边缘经常发生distortion(畸变)
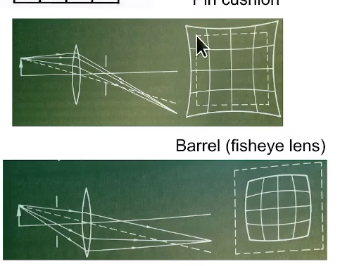
虚线为理想情况
- 图1:聚焦偏外,越角落越边缘的图像越偏外
- 图2:聚焦偏内,越角落越边缘的图像越偏内
The Geometry of Pinhole Cameras(几何)
$$ p=\begin{bmatrix}x\\y\\z\end{bmatrix} \to p'=\begin{bmatrix}x'\\y'\end{bmatrix} $$只要距离足够,透镜和小孔成像都是同一个数学模型
我们完成了三维世界到二维平面的投影
Coordinate systems(坐标系)
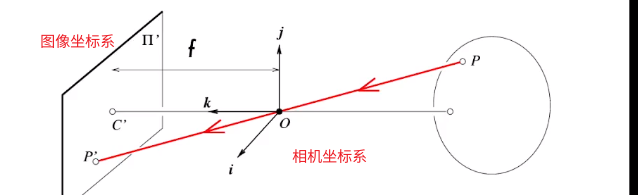
- Off Set:$(x,y,z)\to(\frac{f}{z}x+c_x,\frac{f}{z}y+c_y)$
- $(c_x,c_y)$的存在:相机由于工艺问题,无法保证焦点中心一定在图像中心,因此通过引入参数来进行矫正调整
- From Metric to Pixels:$(x,y,z)\to(k\frac{f}{z}x+c_x,l\frac{f}{z}y+c_y)$
- 我们更偏向乘上系数,使得长度单位变成像素(不同的系数解决了像素是长方形的情况)
- 所以$(c_x,c_y)$也是像素单位
当$z$发生变化时,投影坐标并不是线性变化(倒数),不利于使用线代处理
同时乘上$z$,会丢失$z$的信息
因此引入Homogeneous Coordinates(齐次坐标)
Homogeneous Coordinates(齐次坐标)
$$ (x,y)\to \begin{bmatrix}x\\y\\1\end{bmatrix} $$我们对点坐标,额外增加一个新的维度(二维变三维,三维变四维)
$$ \begin{bmatrix}x\\y\\w\end{bmatrix}\to (\frac{x}{w},\frac{y}{w}) $$$$ (x,y,z)\to(k\frac{f}{z}x+c_x,l\frac{f}{z}y+c_y)\\ (x,y,z)\to(\alpha\frac{x}{z}+c_x,\beta\frac{y}{z}+c_y) $$$$ \begin{bmatrix} \alpha & 0 & c_x & 0\\ 0 & \beta & c_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix}x\\y\\z\\1\end{bmatrix}=\begin{bmatrix} \alpha x+c_xz\\\beta y+c_y \\ z \end{bmatrix} $$$$ P_h'=MP_h $$$z$的信息就能得到很好的保存
Camera Matrix K(相机内参)
$$ M = \begin{bmatrix} \alpha & 0 & c_x & 0\\ 0 & \beta & c_y & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} = K\begin{bmatrix}I & 0\end{bmatrix} $$但由于工艺问题,有时像素平面可能不是一个矩形,而是一个平行四边形,产生了旋转
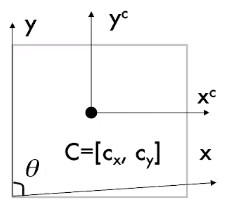
懒得推导了
- $\alpha,\beta,\theta,c_x,c_y$共五个自由度
- 上三角矩阵
World Reference System(世界坐标系)
我们希望世界坐标系转化为相机坐标系,这里我们依旧使用齐次坐标
我们先处理二维平面的情况
-
平移Translation
- $$ P'\to\begin{bmatrix}x + t_x\\y + t_y\\1\end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x\\ 0 & 1 & t_y \\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix}x \\y \\1\end{bmatrix} $$
-
缩放Scaling
-
注意是围绕原点进行缩放
-
当$s_x=s_y$时,称为相似变换
- $$ P'\to\begin{bmatrix}s_xx\\s_yy\\1\end{bmatrix} = \begin{bmatrix} s_x & 0 & 0\\ 0 & s_y & 0 \\ 0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix}x \\y \\1\end{bmatrix} $$
-
-
旋转Rotation
- 同样是围绕原点进行旋转
我们可以组合上述的矩阵:同时进行平移缩放旋转
即对$P$先后进行变换矩阵的左乘即可
对于三维情况:
-
平移Translation
- $$ P'\to\begin{bmatrix} I & T\\ 0 & 1 \end{bmatrix} \begin{bmatrix}x \\y \\z \\1\end{bmatrix} $$
-
缩放Scaling
- $$ P'\to \begin{bmatrix} S & 0\\ 0 & 1 \end{bmatrix} \begin{bmatrix}x \\y \\z\\1\end{bmatrix} $$
-
旋转Rotation
- 绕x轴旋转$\alpha$,绕y轴旋转$\beta$,绕z轴旋转$\gamma$
-
任意绕轴旋转都可以进行分解成绕三轴先后旋转
-
$R = R_x(\alpha)R_y(\beta)R_z(\gamma)$,合成三个矩阵
- $$ P'\to \begin{bmatrix} R & 0\\ 0 & 1 \end{bmatrix} \begin{bmatrix}x \\y \\z\\1\end{bmatrix} $$
在这里,我们一般不考虑缩放(刚体是不会缩放的)
$$ P' \to \begin{bmatrix}R & T \\ 0 & 1\end{bmatrix} $$即可完成旋转后,再平移
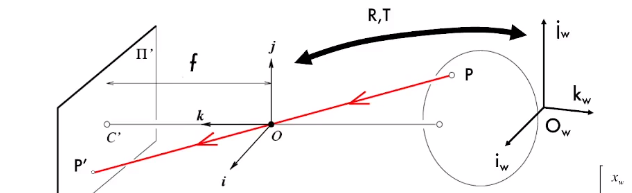
- 从世界坐标系,通过$R,T$转化到相机坐标系
- 从相机坐标系通过投影,转化为图像坐标系
其中$\begin{bmatrix}R & T\end{bmatrix}$被称为外参数
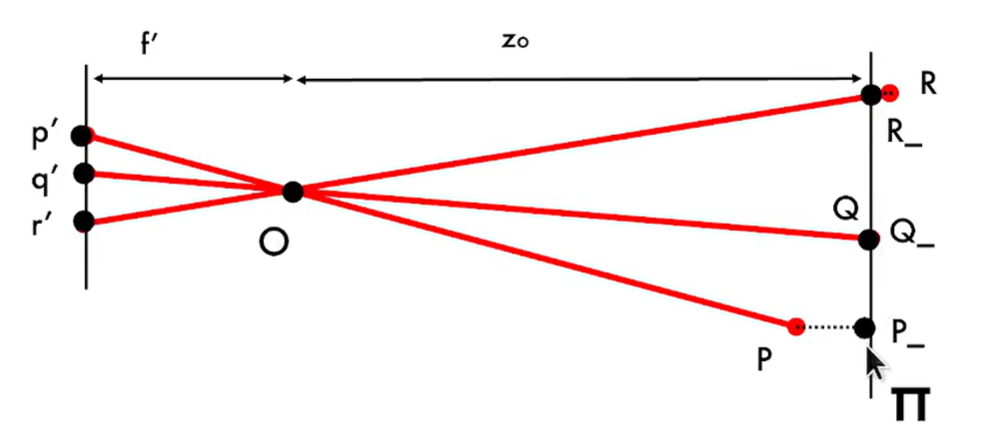
Weak Perspective Projection(弱透视投影)
当物体离相机足够远时,深度$z$其实可以近似为一个常数$z_0$,从而简化计算
L8: Fitting and Matching
Fitting
Choose a parametric model to fit a certain quantity from data
Estimate model parameters
Critical issues
- noisy data
- 数据中存在的随机误差或不确定性,测量、记录或传输过程中的各种因素引起
- 对整体趋势影响较小
- 处理噪声数据的方法包括平滑技术(如移动平均)、滤波方法、数据清洗等
- outliers
- 数据集中与其他观测值明显不同的值,测量错误、录入错误、实际现象的稀有事件
- 具有明显的偏离,可能对分析结果产生较大的影响
- missing data
Techniques
目标:拟合点集$(x_i,y_i)$
Least Square methods(最小二乘法)
- 直线模型:$y-mx-b = 0$
- 找到$(m,b)$使得最小化误差$E = \sum(y_i-mx_i-b)^2$
对$h$求导
$$ \frac{dE}{dh} = -2X^TY+2X^TXh=0 $$$$ h = (X^TX)^{-1}X^TY $$但是这样是代数意义上的最优解
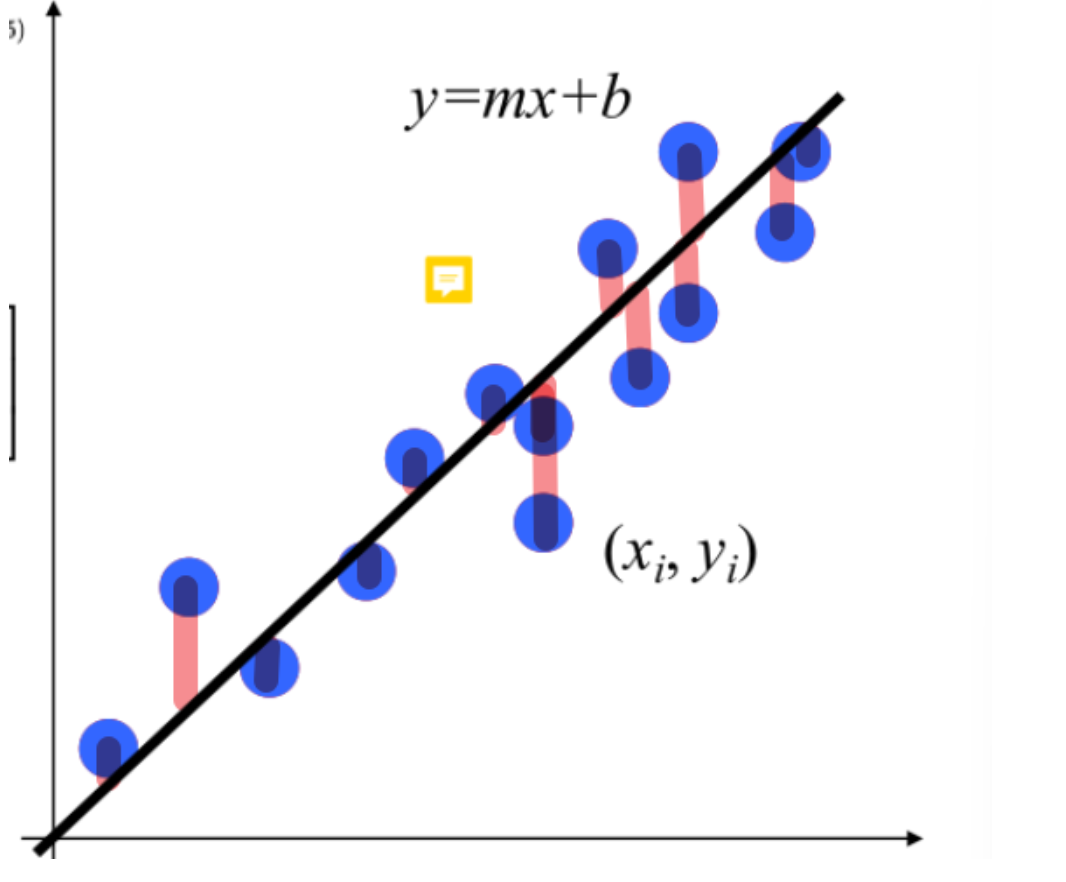
考虑几何意义上的最优解:
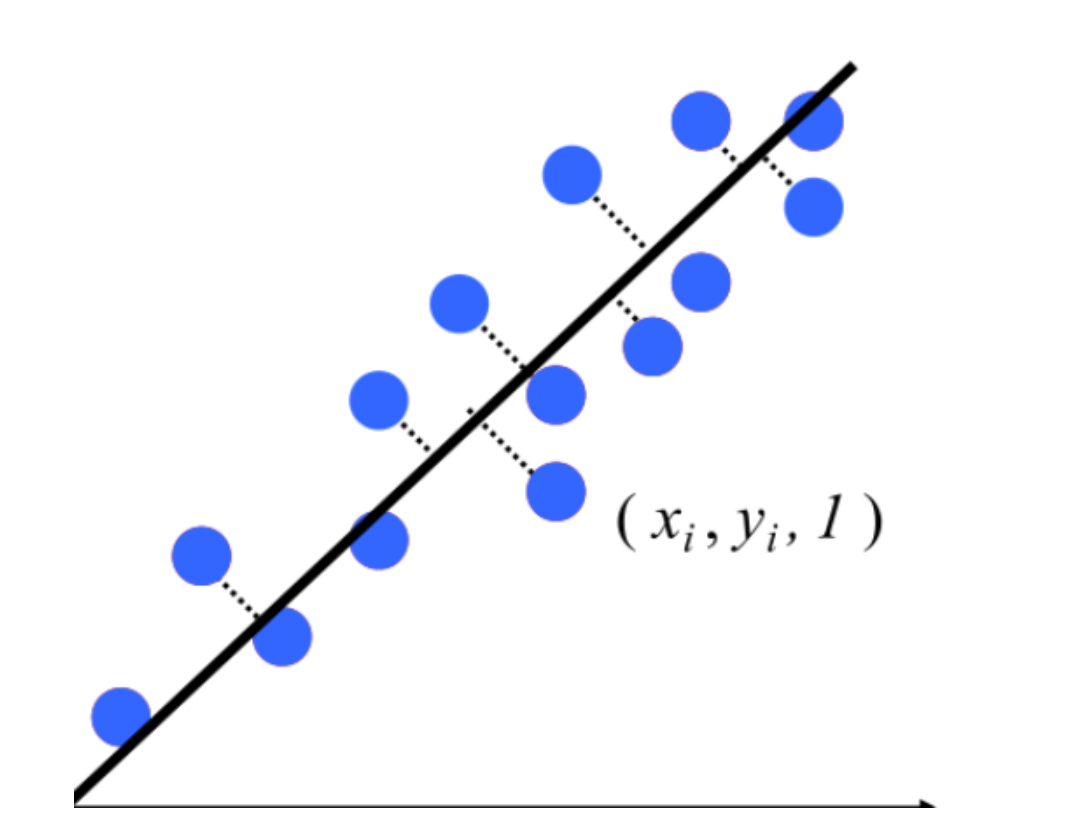
我们可以$a,b$的存在表示了斜率,因此我们可以通过类似归一化的操作,使得$\sqrt{a^2+b^2}$为1,或者为一个定值
因此我们事实上只需要关心$|ax+by+d|$,代表了相对大小,不需要具体的真实值
故定义:$E = \sum |ax+by+d|^2$
我们需要寻找最优的$(a,b,d)$
令矩阵
$$ A = \begin{bmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ ...&...&...\\x_n&y_n&1\end{bmatrix}\\ h = \begin{bmatrix} a\\b\\d\end{bmatrix} $$则问题转化为:最小化 $||Ah||$,并且限制$||h|| = 1$
使用SVD分解即可完成优化问题(留坑待填)
最后:
- 噪声:鲁棒的
- 外点:影响巨大
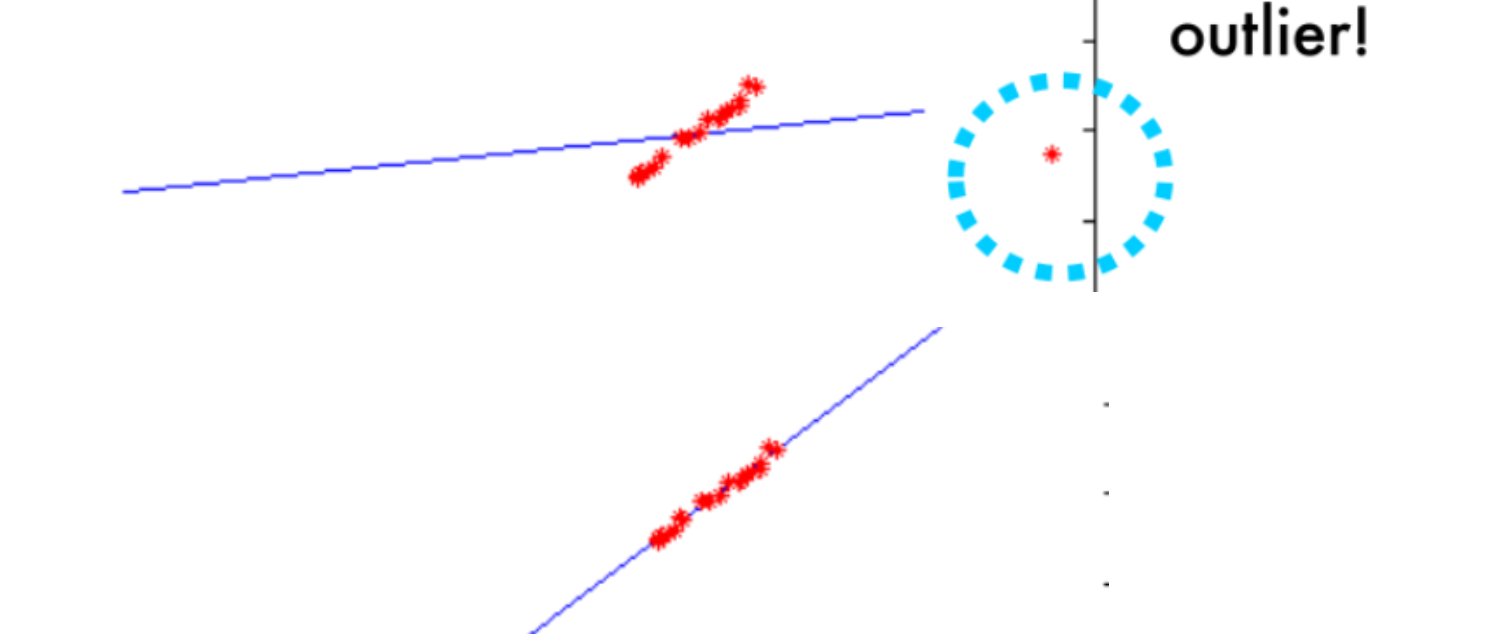
conclusion: Least Square is not robust w.r.t. outliers.
“w.r.t.” 是英文表达中的缩写,意思是 “with respect to”,翻译成中文是 “关于”、“针对”、“就…而言” 等等。
Least Squares: Robust Estimators (鲁棒估计器)
令残差$\mu = ax+by-d$
$$ \rho(u;\sigma) = \frac{\mu^2}{\sigma^2+\mu^2} $$
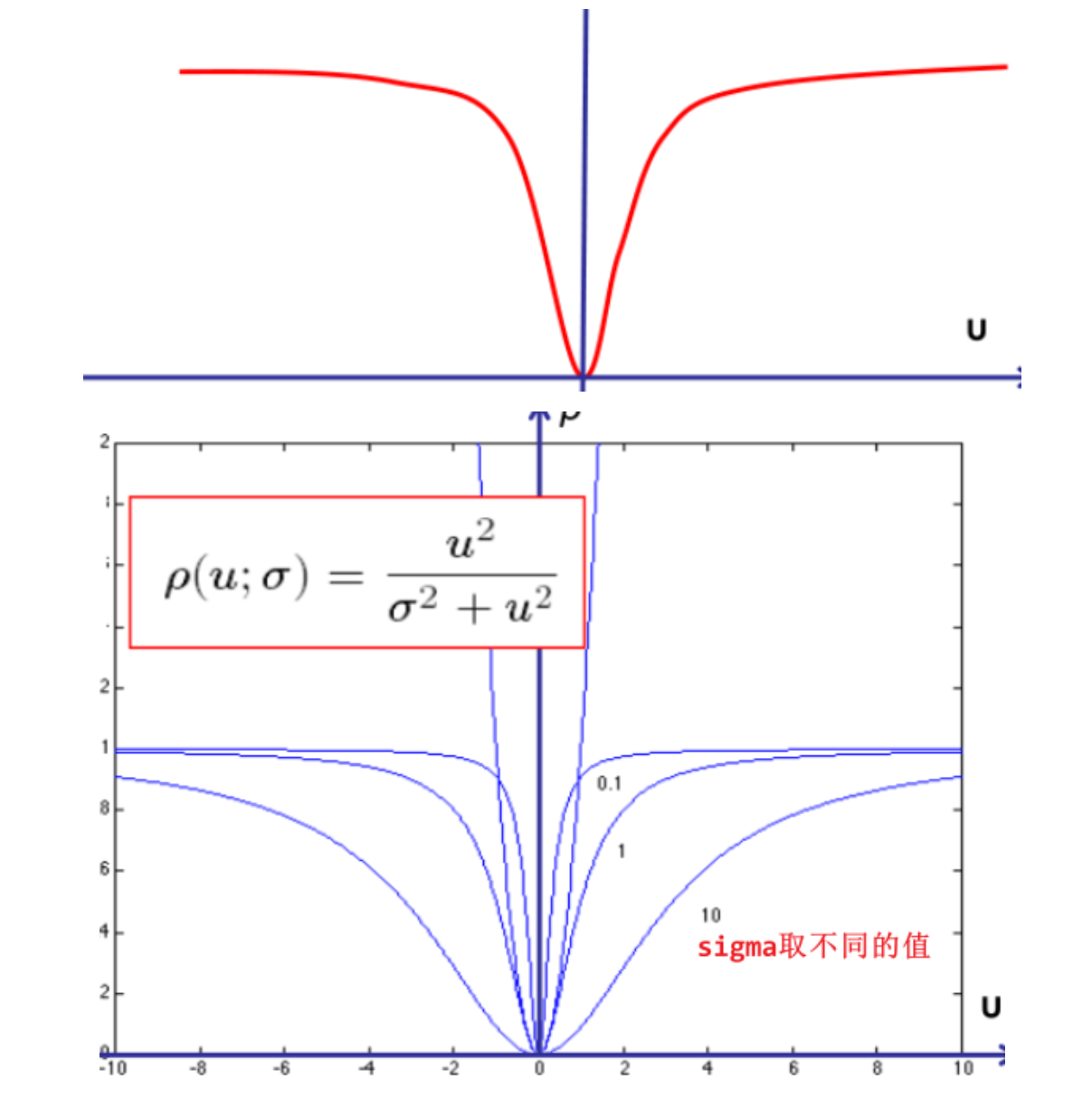
- $\mu$越大,函数值接近1
- $\mu$越小,函数是一个关于$\mu^2$的函数
较大的残差,原本会极大影响损失函数的值
通过此方法,我们限制了大残差的贡献,从而降低了对损失函数的影响,故能拟合的鲁棒性提升
RANdom SAmple Consensus(RANSAC)
- 假设1:嘈杂的数据不会为任何单一模型投一致的票
- 假设2:有足够的数据点来商定一个好的模型
我们定义好阈值$\delta$,与给定直线的距离在阈值范围内的点,被称为内点;否则是外点
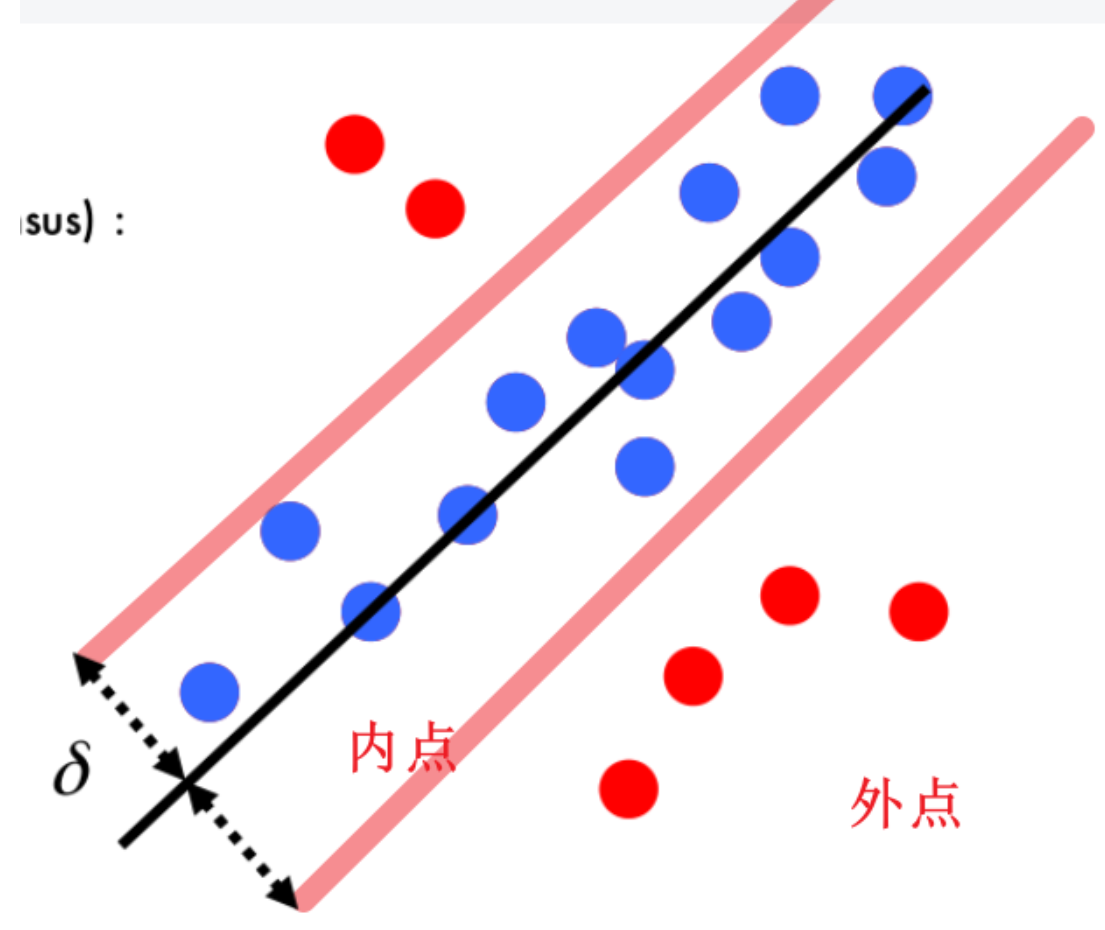
算法流程
- 随机选择出需要确定模型的最小数量的点(例如:确定直线需要两个点,因此随机两个点)
- 对于随机选出的点,计算出模型
- 计算出内点和外点
重复多次,外点数量最小的模型即为我们需要的
因此我们比较好奇重复多少次可以基本保证能找到最优解
设重复次数为$N$,算法成功概率为$p$(一般取0.99),$e$表示内点数量与点数之比,$s$表示采样点的数量
$$ 1-p = (1-e^s)^N $$$$ N = \frac{\log (1-p)}{\log (1-e^s)} $$
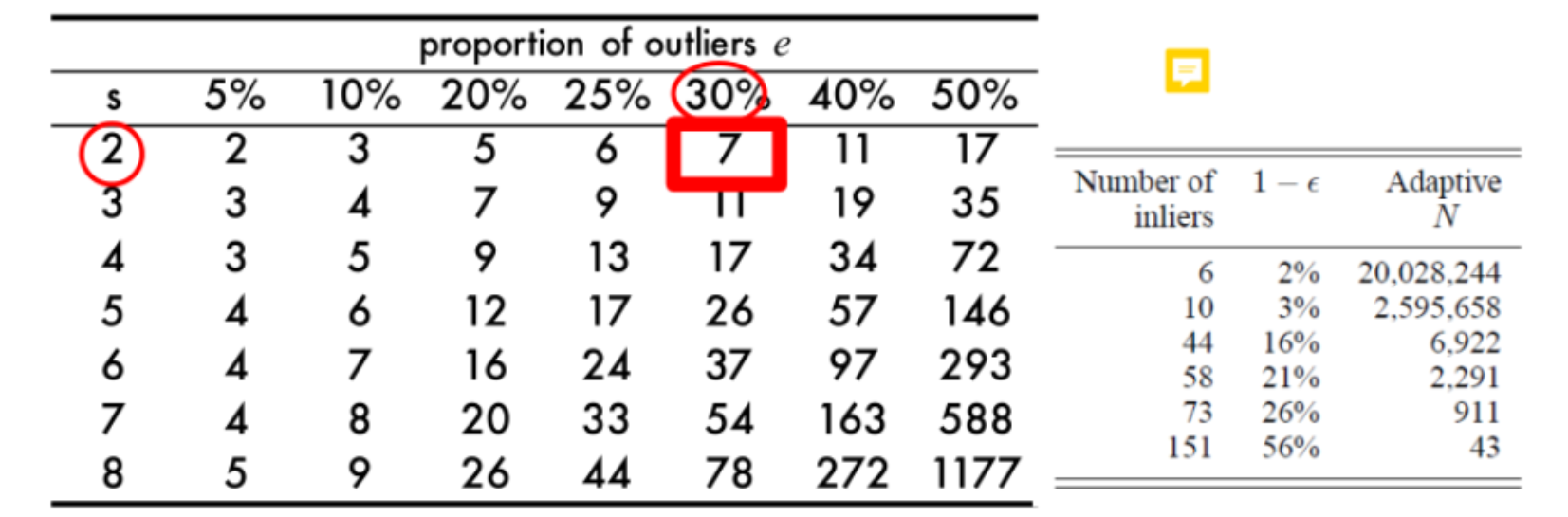
不管是需要采样的点变多,还是内点比例下降,都会使得次数增加
conclusion: Cannot be used if ratio inliers is too small
但对于大部分场景,外点是占较大部分的,因此很难使用
Hough transform(霍夫变换)
设一条直线:$y=mx+n$,其中$(x_i,y_i)$是该直线上一点
我们考虑将$m,n$看作自变量与因变量:$n = -x_im-y_i$
因此我们得到了
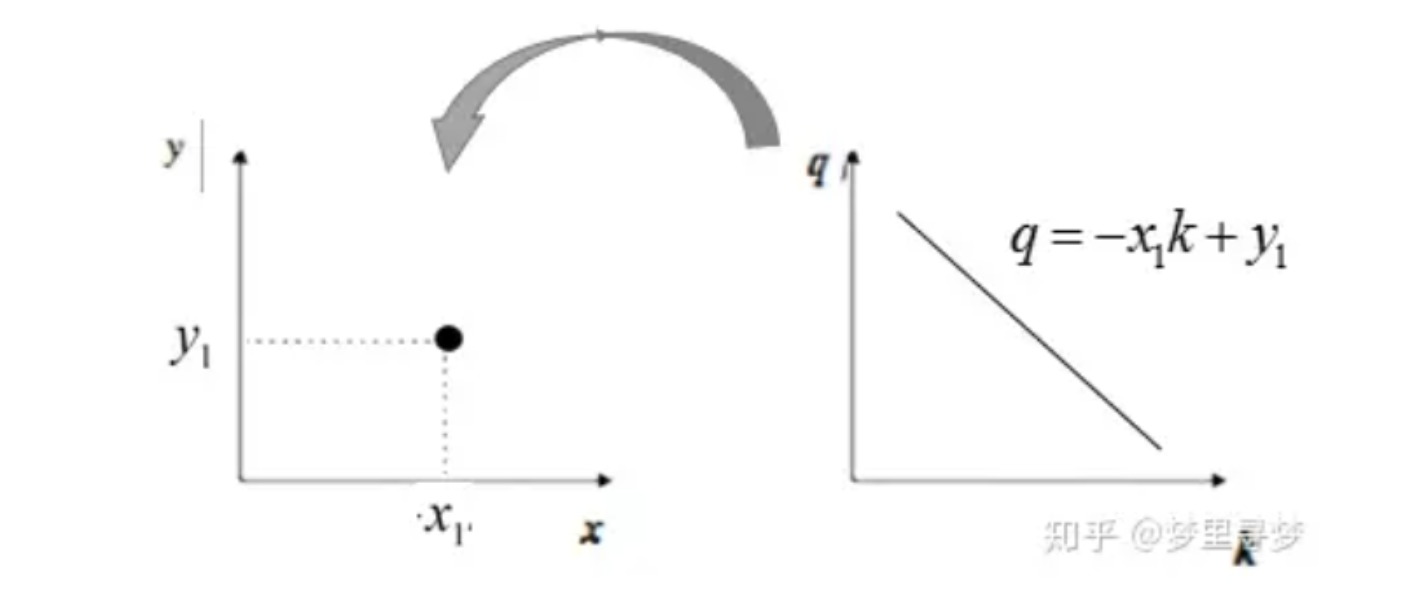
经过霍夫变换后得到的被称为是霍夫空间
笛卡尔坐标系中的一个点,对应霍夫空间中的一条直线
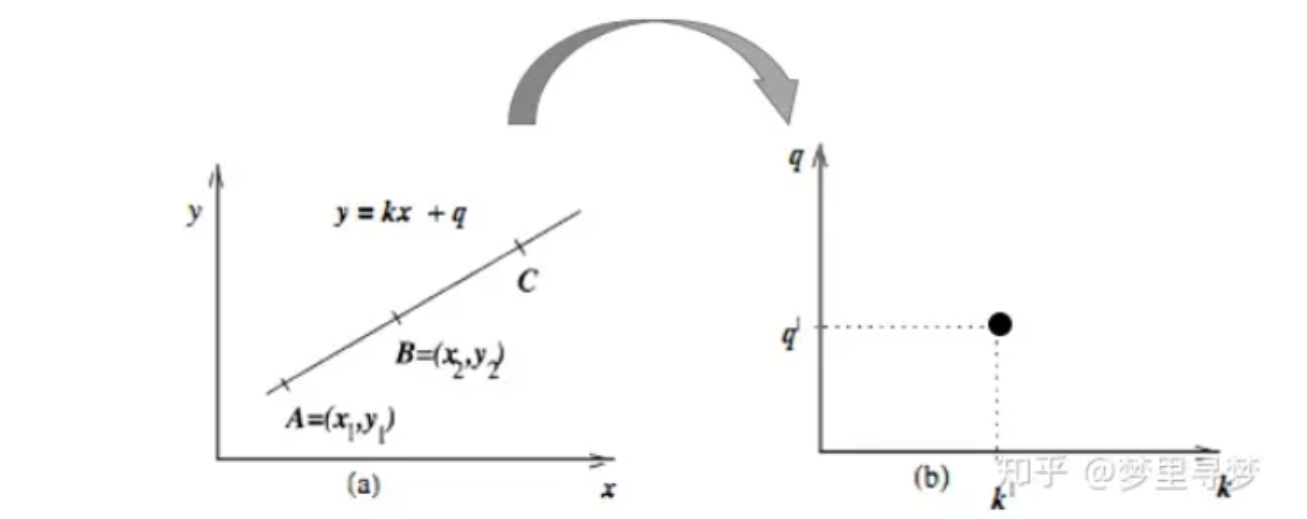
同理,笛卡尔坐标系中的一条直线,对应霍夫空间中的一个点
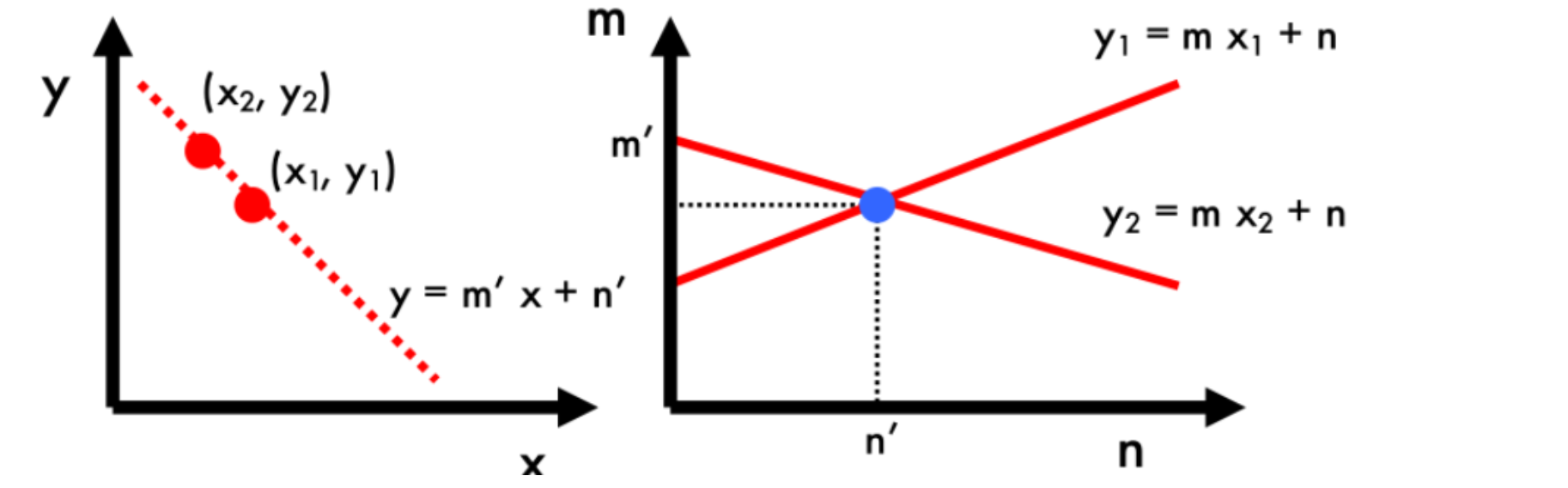
因此在笛卡尔坐标系中,同一直线上的点,其在霍夫空间中将交于同一点
理论上我们只需要知道哪些点被投票得最多,这条直线就是我们需要的
但问题还很多:我们无法表示垂直的线
考虑切换为极坐标系
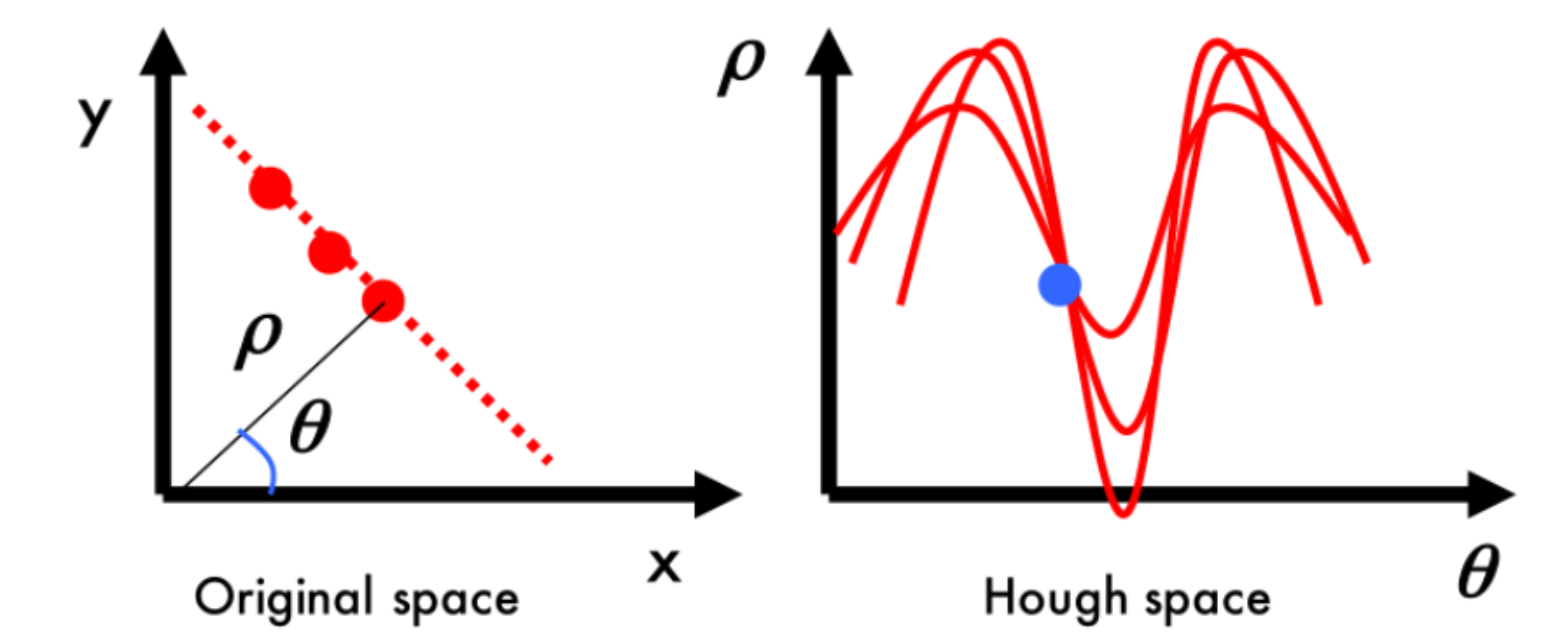
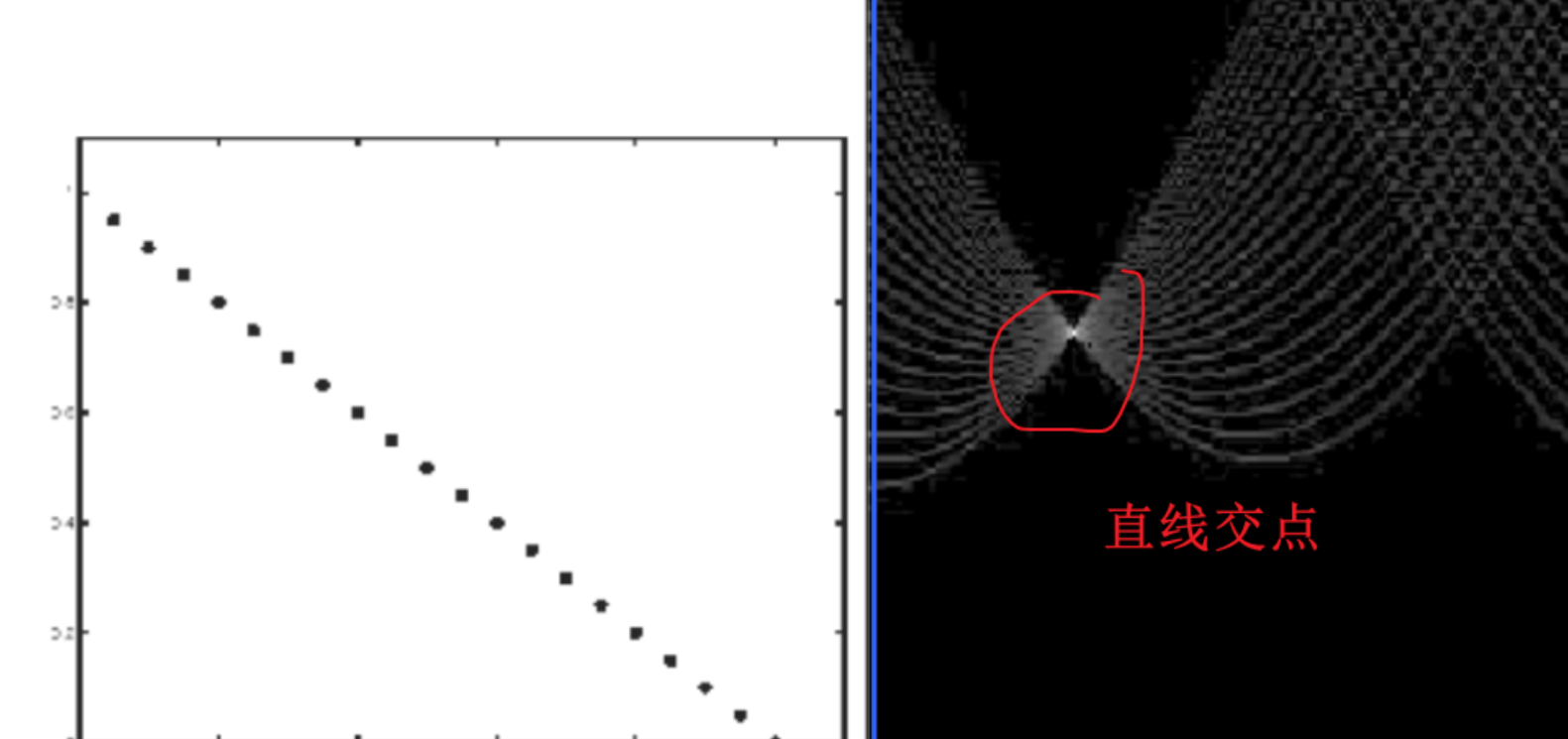
我们将霍夫空间看作一个网格
其中高度为原图像对角线长度($\rho$的最大值),宽度为$\theta$的最大值$2\pi$
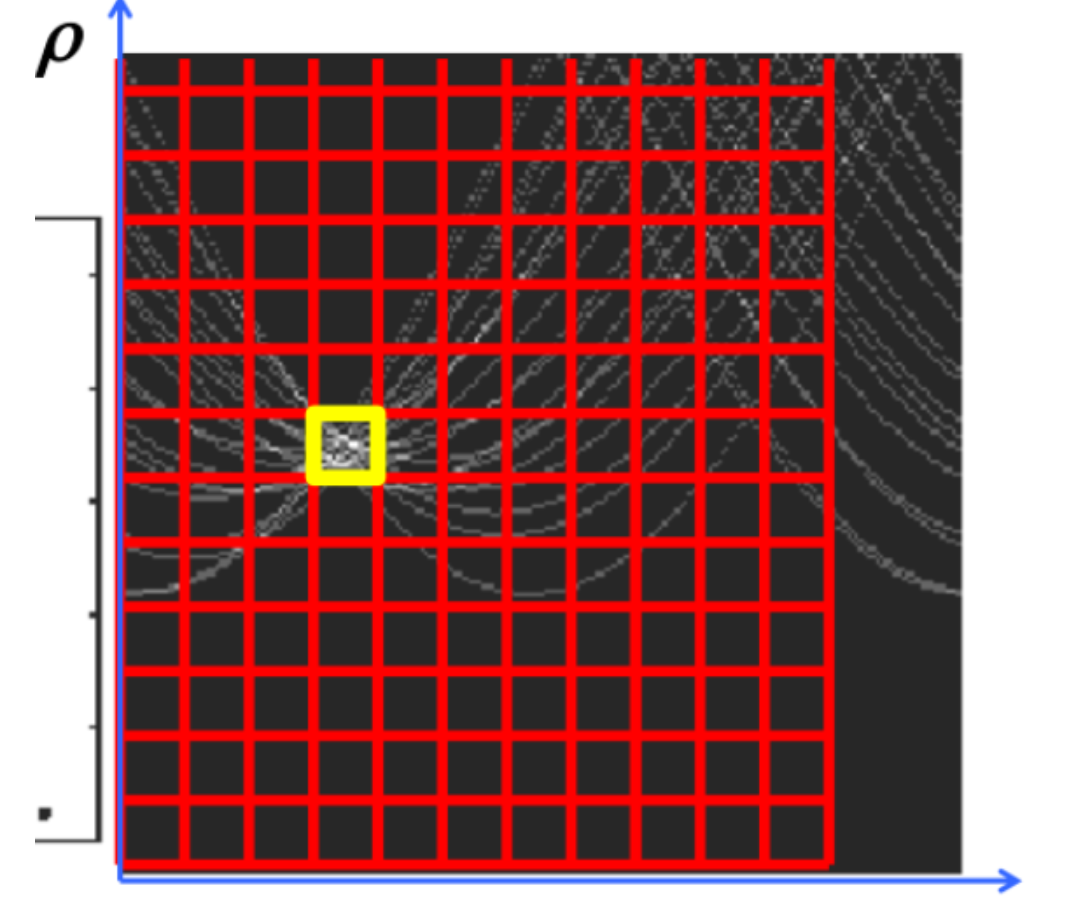
枚举网格点,估计一下其中的交点数量
对于高维数据非常难以处理
L9. Detectors and descriptors
Detectors
Edge detectors
Edge产生的要素
- 深度不连续性
- 表面方向不连续性(物体表面不同部分的朝向或法线方向发生突然变化)
- 反射率不连续性(即,表面材料性质的变化、颜色)
- 光照不连续性(例如,高光; 阴影)
边缘检测的例子

检测标准
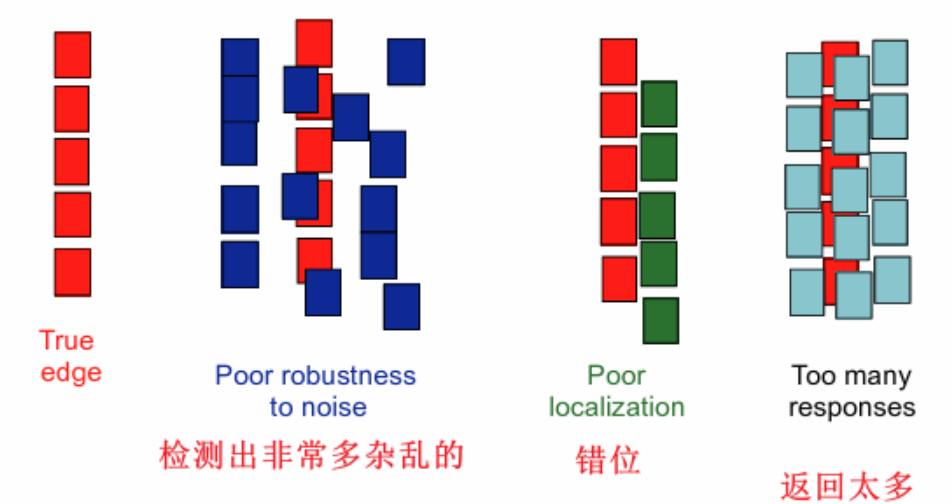
- Good detection accuracy:不误检测噪声,漏检测真实边缘
- Good localization:检测边缘应该尽可能接近真实边缘
- Single response constraint:单一的回应
Detectors的设计
- 使用导数,定义了梯度较高(也就是变化较为激烈)的地方
- 对图像进行了平滑处理,提取导数之前减少噪音
因为是离散的,所以单位长度是一个像素,我们对一个像素作一个差值就是变化率,即导数
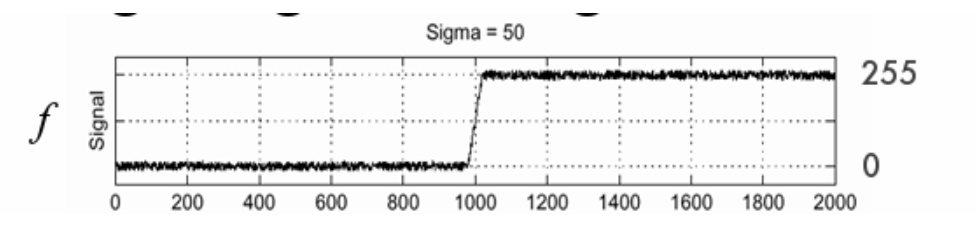
考虑如上的一个图像,我们若直接求出导数图像,你会发现并没有特别显著的大导数
原因是本身图像的波动大概就是5左右,而上升部分的差值也差不多是5
所以你会发现导数基本都一样
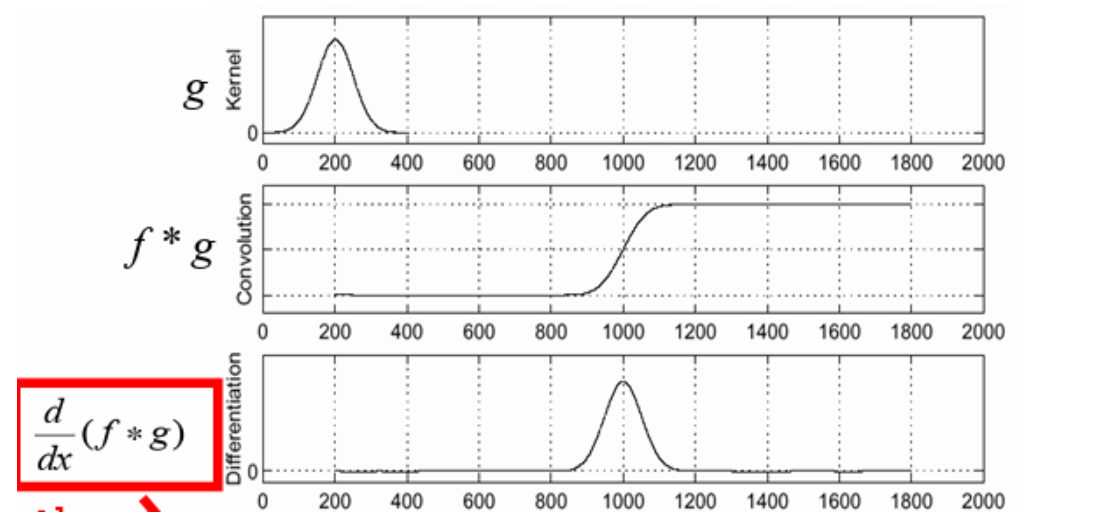
因此我们使用高斯模糊的卷积核进行平滑处理
$$ S = \bigtriangledown(g\ast I) = (\bigtriangledown g)\ast I \\ = \begin{bmatrix} \frac{\partial g}{\partial x} \\ \frac{\partial g}{\partial y} \end{bmatrix}\ast I = \begin{bmatrix} g_x\ast I \\ g_y\ast I \end{bmatrix} \\ = \begin{bmatrix} S_x & S_y \end{bmatrix} $$Corner/blob detectors
- 可重复性:尽管存在几何和光度变换,但同一特征可以在多幅图像中被找到。
- 显著性:每个特征都位于图像的“有趣”区域。(反正基本不是空白区域)
- 局部性:一个特征占据图像的“相对较小”区域。
Harris corner detector
在窗口位置变化时探索窗口内的强度变化
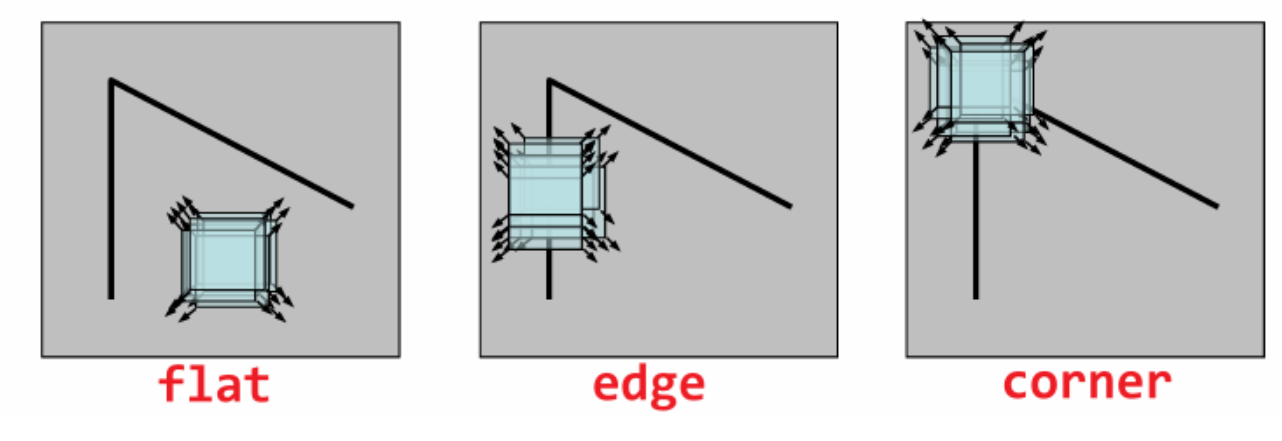
- flat:在所有方向上都没有变化
- edge:沿着边缘方向没有变化
- corner:在所有方向上都有显著变化

我们无法知道corner的尺度变化
Blob detection
回到边缘探测,我们可以把卷积后的结果的导数
修改为二阶导
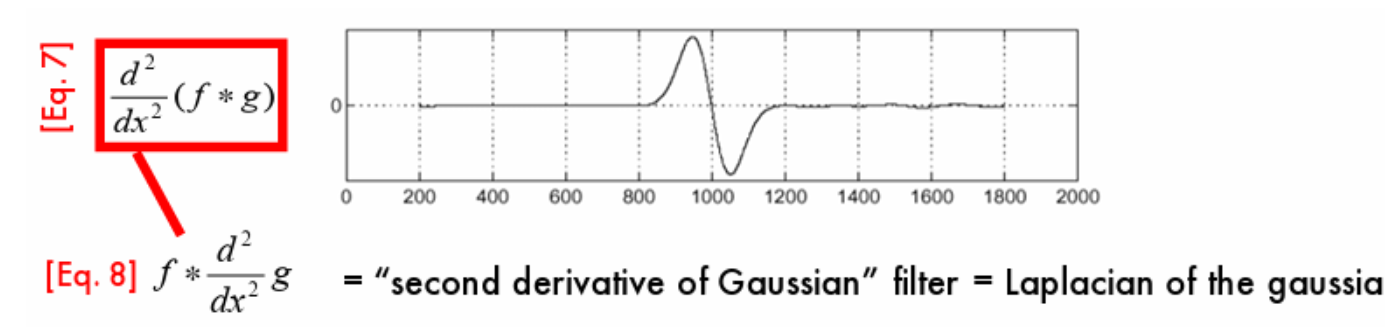
因此我们的高斯算子可以换成拉普拉斯算子(高斯的导数)

对原图像使用拉普拉斯算子进行处理即可
因此对于一个比较宽的图形,两侧边缘会分别导出两个波动
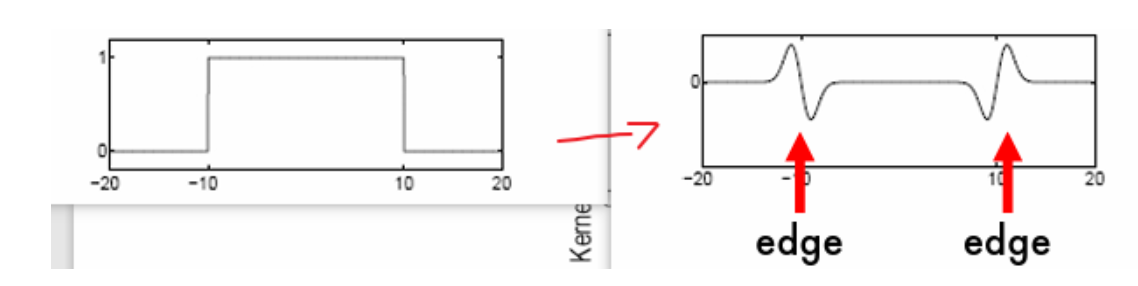
我们先尝试固定拉普拉斯算子,当图形宽度变化时
某种情况下,两个波动会融合在一起,并且幅度最大值取在了图形中央
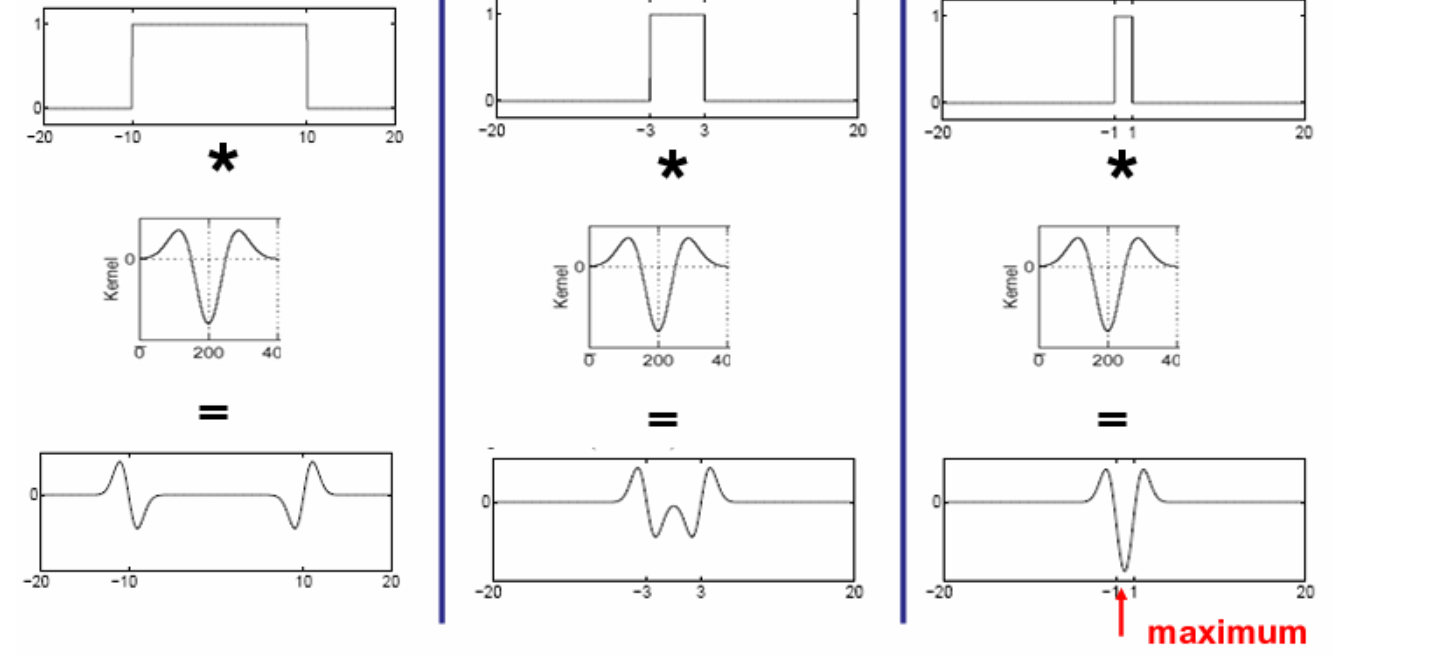
所以我们调一下参数,就可以找到幅度最大的点,从而估计出尺度大小
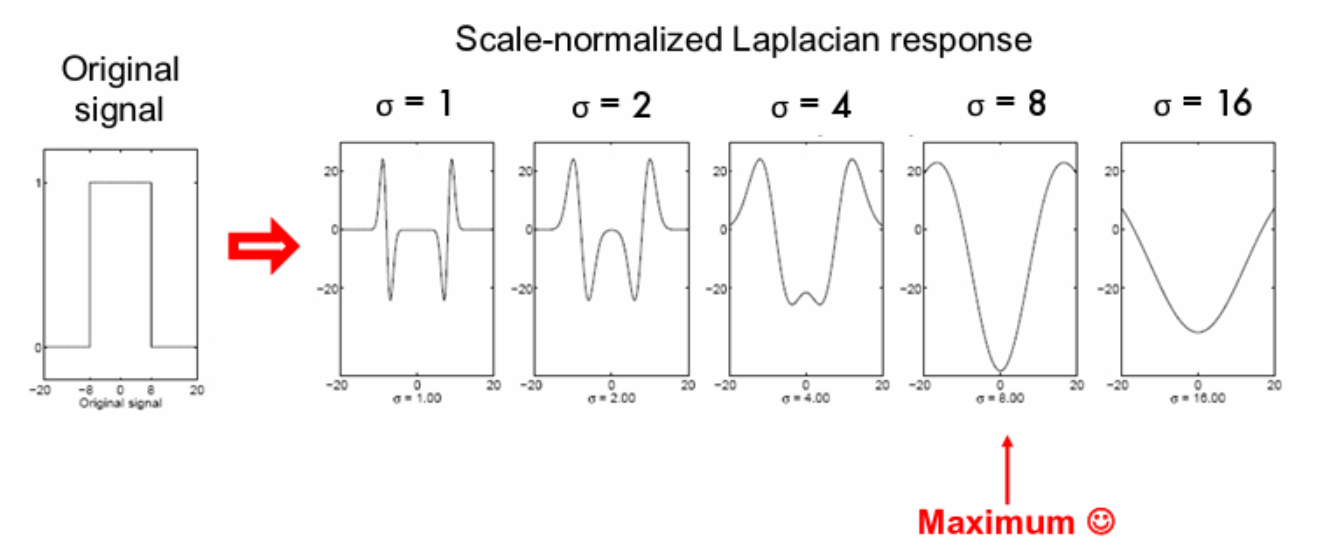
并且对于半径为$r$的圆,取到最大值的参数是可以计算的
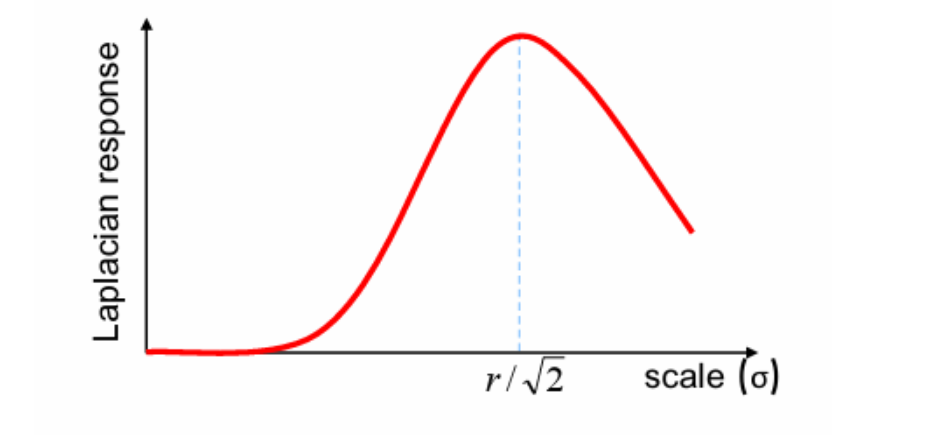
DoG
高斯差分,你只需知道这个算子会更常用一点
Descriptors
描述信息一般需要:
特征保证
- 光照不变性(Invariant w.r.t Illumination):特征应该不受光照变化的影响。
- 姿势不变性(Invariant w.r.t Pose):特征应该不受物体姿势变化的影响。
- 尺度不变性(Invariant w.r.t Scale):特征应该不受尺度变化的影响。
- 类内变异不变性(Invariant w.r.t Intraclass variability):特征应该能够在相同类别的不同实例之间保持稳定性。
特征要有
- 高度独特性(Highly distinctive):特征应该具有足够的独特性,以便在大型特征数据库中能够以高概率找到其正确匹配的特征。
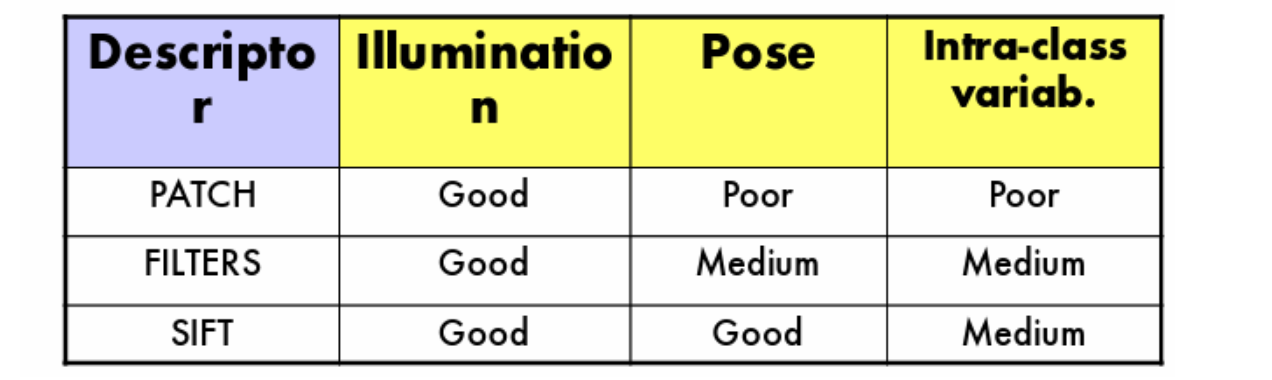
Simplest Descriptor - Patch
图像中的一个小区域或局部区域,通常由一组相邻像素组成
将特征周围的像素$n\times m$的小图片展开为$[1,nm]$大小的一维向量$w$
$$ w = \frac{w-\bar{w}}{||w-\bar{w}||} $$减去均值除以模长
无论图像的光照条件如何变化,这种归一化保证了描述符的生成不会受到影响,从而增强了描述符的稳定性和可靠性
缺点
- 对于位置、姿势、尺度和类内变异的小变化敏感
- 特征区分度较差
Filter
提供卷积核做点事情,然后提取特征
只能说鲁棒性有所提升
SIFT
大致理解即可,并不准确
- 使用DoG确定位置和特征尺度
对于一个$N\times N$的窗口,我们对每个像素计算梯度
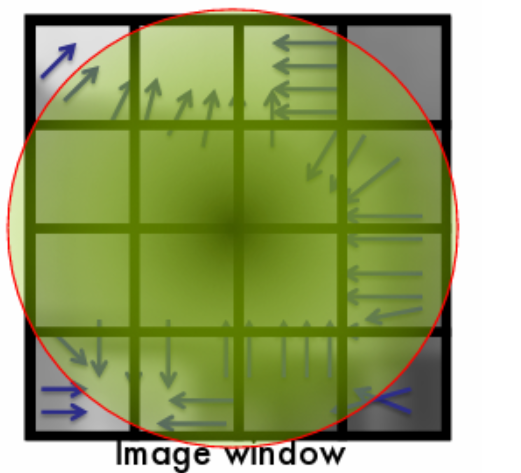
我们把$[0,2\pi]$分成若干份,对所有方向进行计数
数量最多的即为主方向
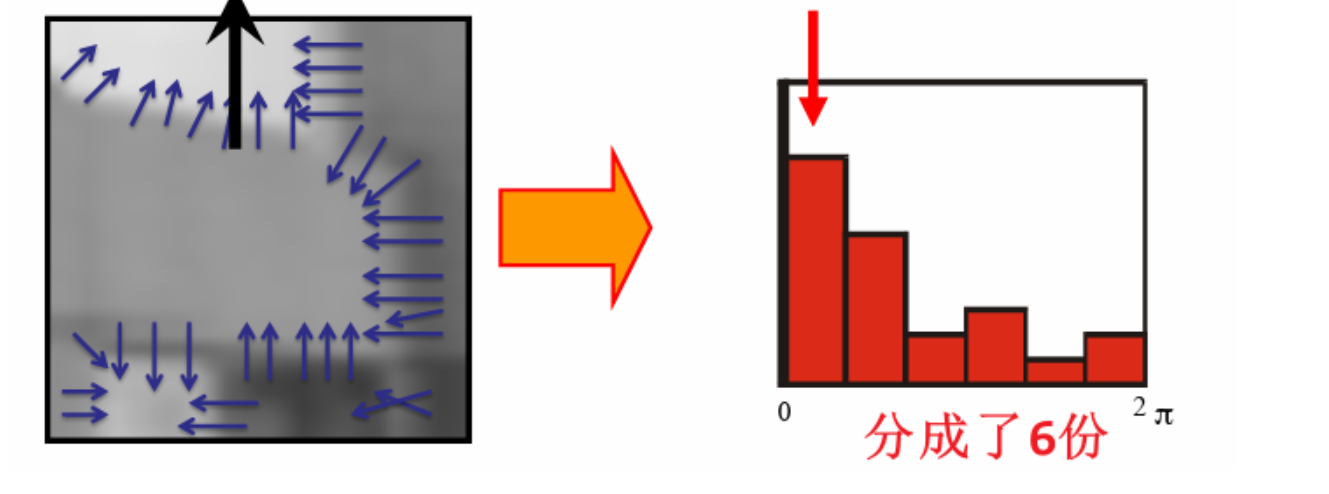
那么只需要按照主方向的角度进行旋转即可
打包后得到的向量即为描述符
显然
- 强度:DoG的归一化、梯度足够处理
- 姿势:按照主方向把所有箭头旋转成一样的角度,无视了姿势变化
- 尺度:DoG处理完毕
- 类内变异:直方图有一定的粗略计算,有一定鲁棒性
L11. Visual recognition
数学补坑
SVD分解(未完成)
卷积
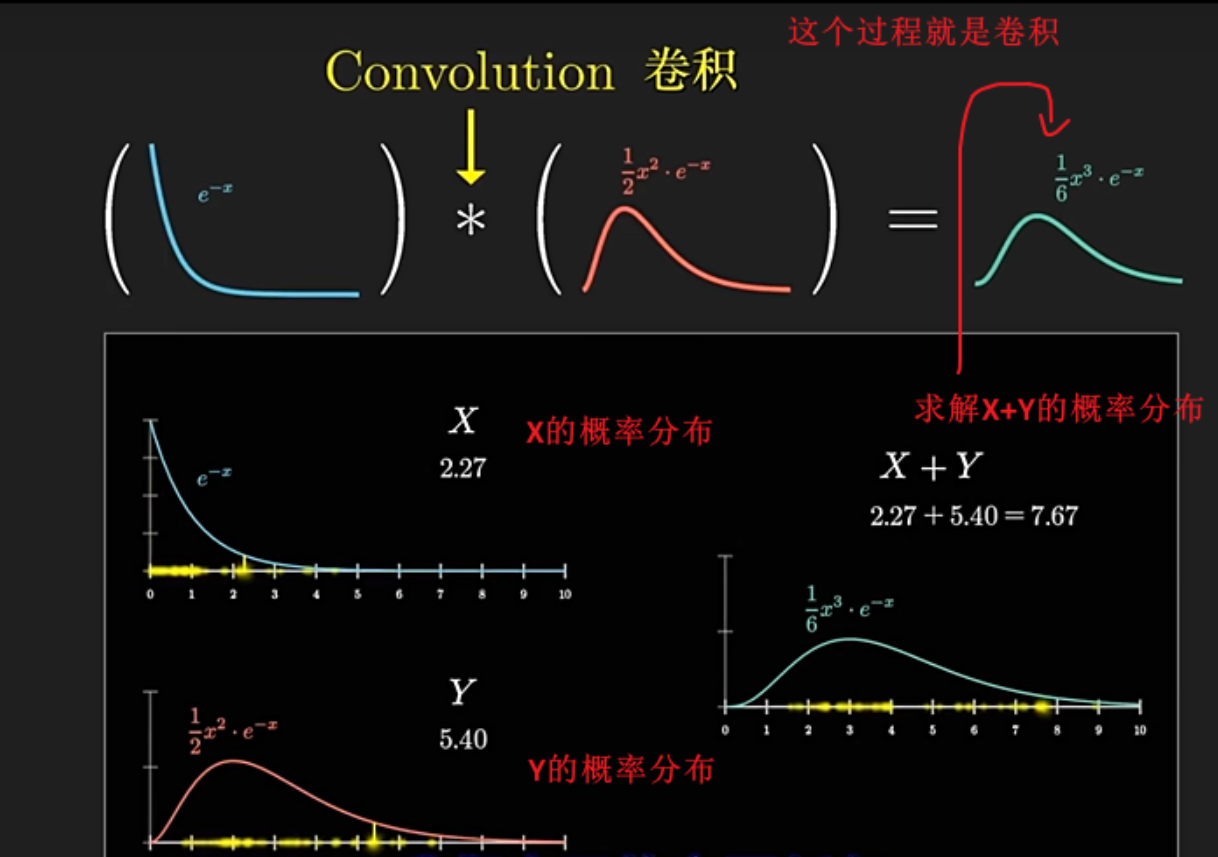
在这里我们主要理解一下离散的情况即可
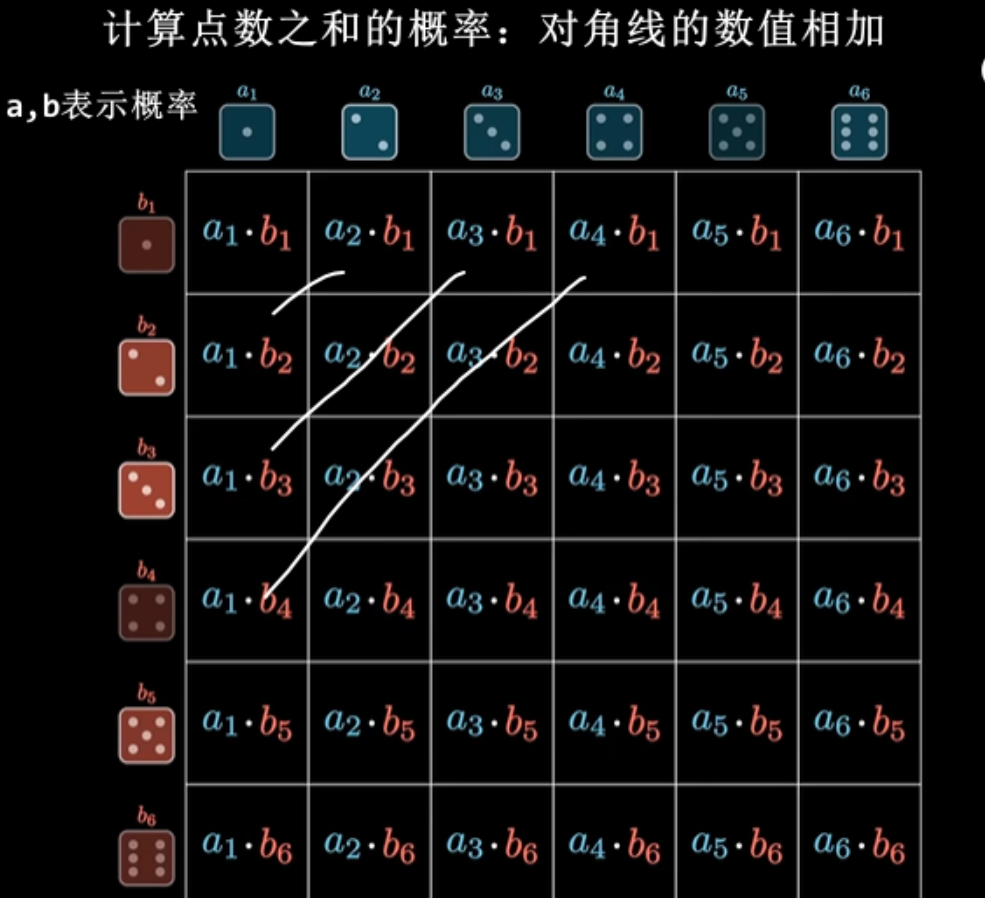
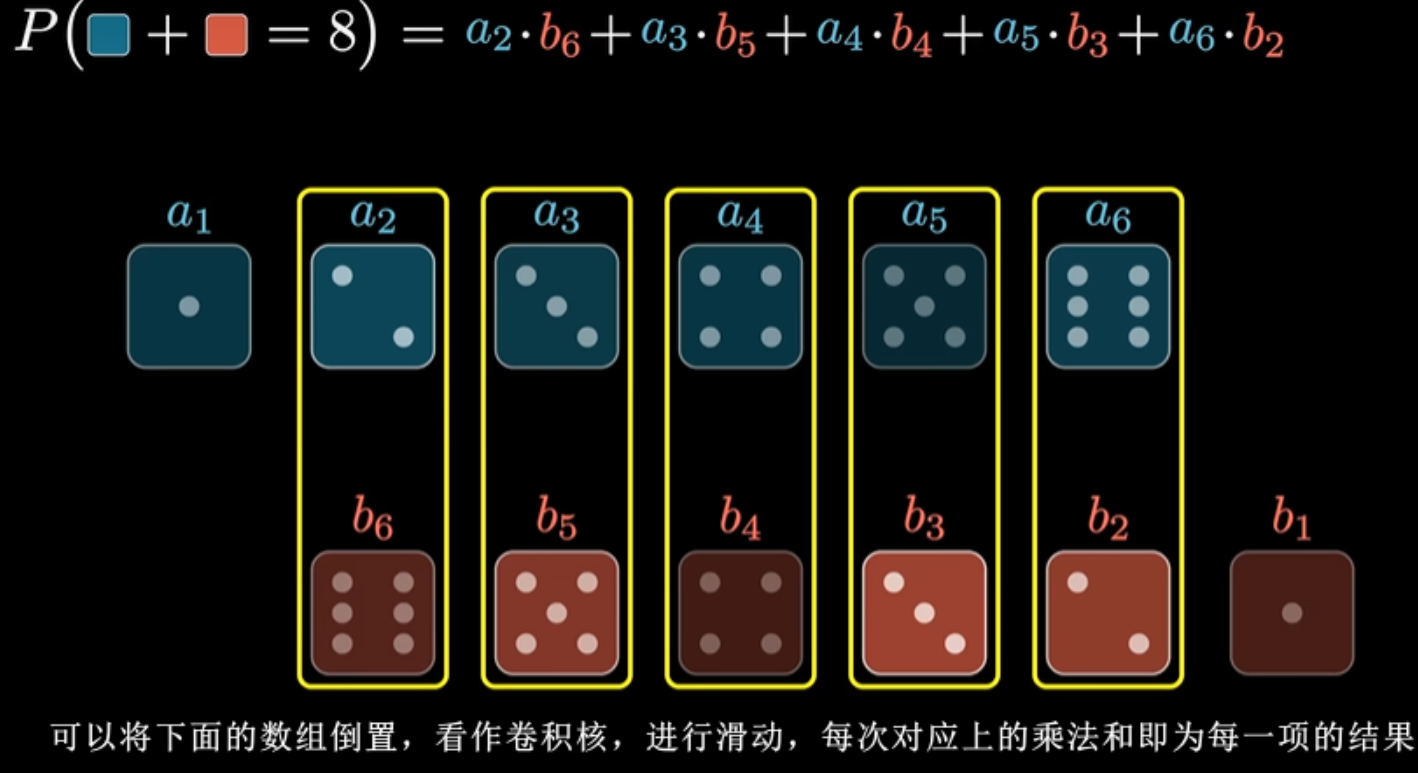
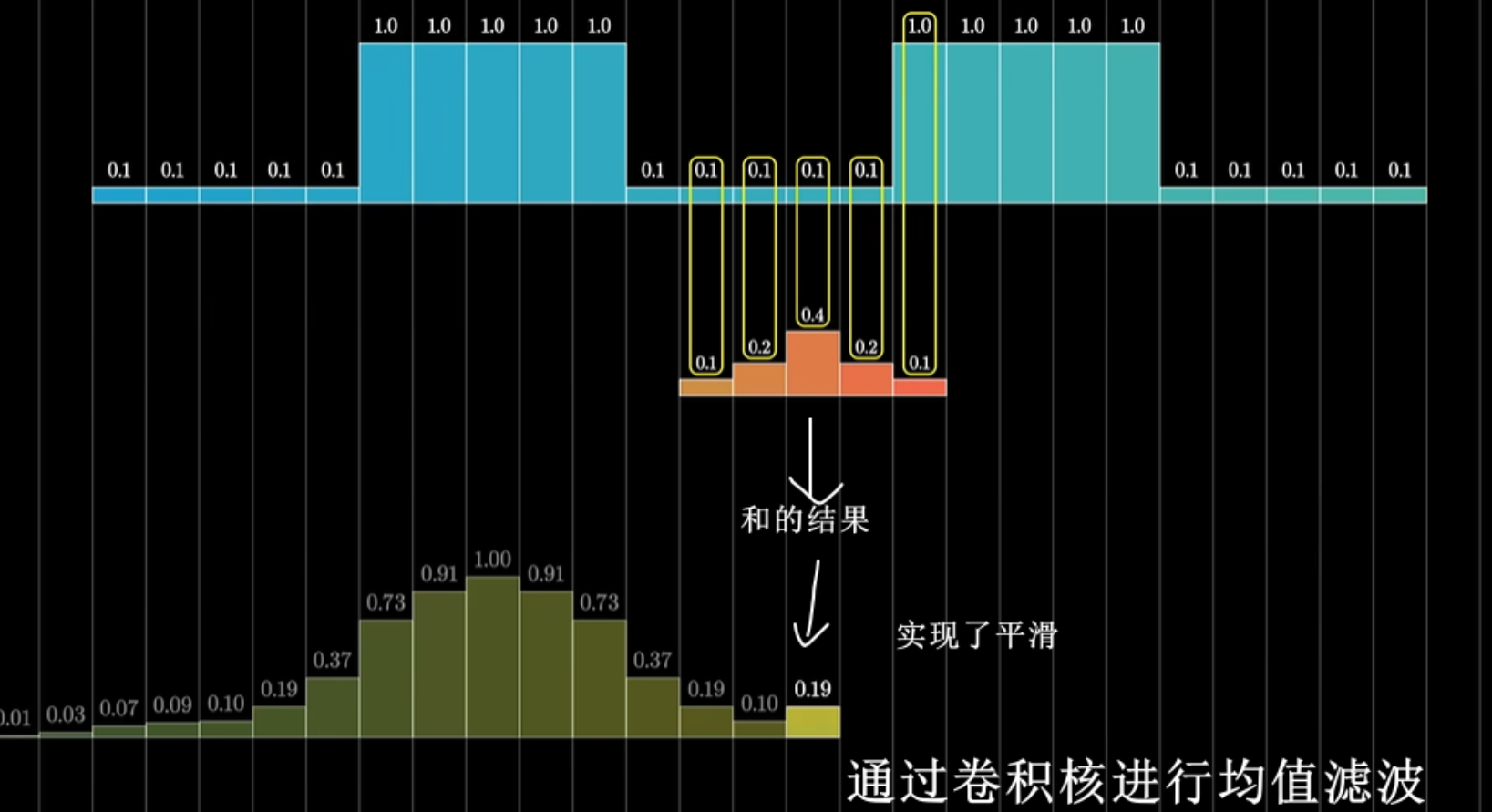
高斯模糊:
在二维图像上,使用一个$n\times n$的卷积核,卷积核的值从中心开始符合二维高斯分布,对整个图像的颜色进行加权平均