Large Language Diffusion Models
[TOC]
Intro
理想情况下,无限数据+无限模型容量+正确训练 ,可以收敛到真实分布
因此不管是ARM还是DLM,只要是合格的条件生成模型,都能学到真实语言分布
因此指令跟随、上下文学习并不是ARM的专利
Approach
概率公式
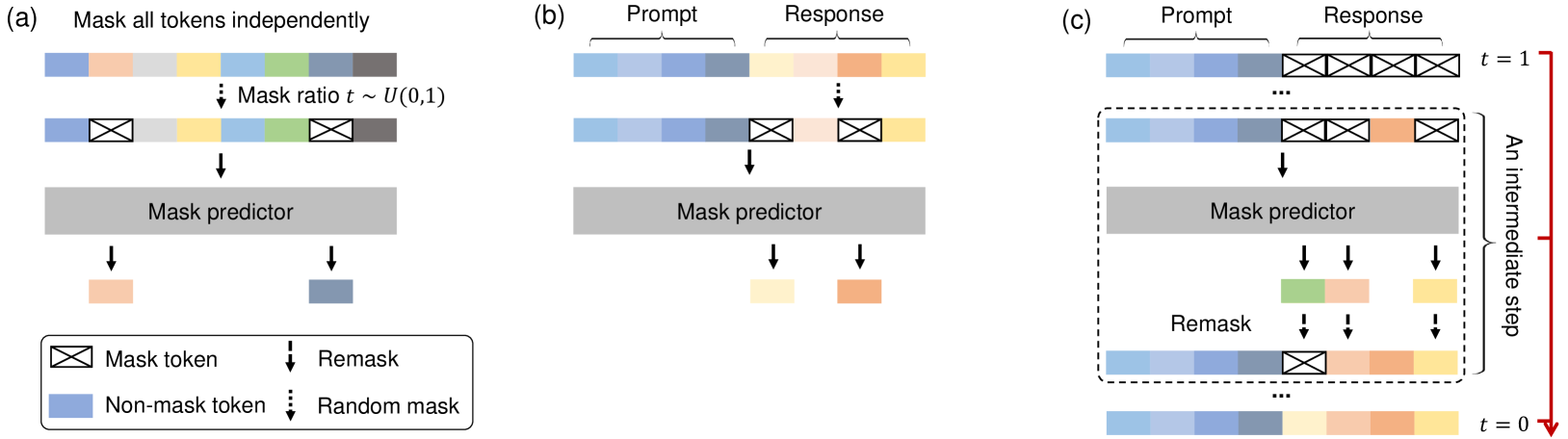
前向过程Forward Process
序列中逐渐添加mask,直到所有序列全部masked
- 每个标记有一定概率masked,或者保持unmasked状态
- 给定原始数据$x_0$,随机采样的一个时间点$t \in [0,1]$
- $t=0$表示起点,全部token都是unmasked
- $t=1$表示终点,全部token都已经masked
- 序列中每个token的masked概率就是$t$
- 该时刻的序列被定义为$x_t$
Bert的mask比例是固定的
反向过程Reverse Process
参数为$\theta$的模型,生成序列$x_0$的概率$p_\theta(x_0)$就是我们需要训练的模型
我们希望其尽可能接近真实数据的分布$p_{data}(x_0)$
- 反向过程的目标:$x_{t=1}$出发,恢复$x_0$
- 方法:通过
mask predictor,逐步填充masked token
Mask Predictor
LLaDA的核心是一个mask predictor
其中的·表示一个占位符
例如:
|
|
则$p_\theta(\cdot \mid [I,[MASK],cats])$ 就是一个基于词表的概率分布表
| token | p |
|---|---|
| like | 0.9 |
| eat | 0.1 |
此时Mask Predictor会对所有[MASK]进行预测
不像ARM只预测一个token
假设序列为:$(x_t^1, x_t^2,…,x_t^L)$
我们的目标即为,对于masked位置$i$,最大化概率:
其中$x_0^i$就是原序列的ground truth
损失函数
对于单个masked位置,我们希望概率尽可能大
因此需要使用交叉熵损失
补习一下交叉熵
假设真实分布是$q(y)$,模型分布是$p_\theta(y)$
交叉熵定义为:
$$ H(q,p_\theta) = -\sum_y q(y)\log{p_\theta(y)} $$在该任务下,$q(y)$是一个独热分布
$$ q(y) = \left\{\begin{matrix} 1&,y=x_0^i \\ 0&,otherwise \end{matrix}\right. $$代入得
$$ \mathcal{L}(x_0^i,x_t) = -\log p_\theta(x_0^i\mid x_t) $$
故整体的损失就只需要对所有masked位置求和
其中$1\left[ x^i_t=M\right] $表示指示函数,确保代入计算的数值是[MASK]
但是这样是不合理的,序列中[MASK]越多,损失似乎会越大
因此需要做一下归一化
对于$x_t$,其在该时刻会有$tL$个token被masked
因此需要代入一个$\frac{1}{t}$(值得一提的是,$\frac{1}{t} \geq 1$)
$$ \mathcal{L}(x_0,x_t) = -\frac{1}{t}\sum_{i=1}^L1\left[ x^i_t=M\right] \log{p_\theta\left( x_0^i\mid x_t\right)} $$建立关于模型参数$\theta$的损失函数则有:
$$ L(\theta) \triangleq -\mathbb{E}_{t,x_0,x_t}\left[\frac{1}{t}\sum_{i=1}^L1\left[ x^i_t=M\right] \log{p_\theta\left( x_0^i\mid x_t\right)}\right] $$- $\triangleq$代表
定义为
这里不是在陈述一个“事实”,而是在引入损失函数的定义。
如果写$=$,读者可能会以为“这是某个推导得到的等式”;
如果写 $\triangleq$,读者一眼就知道:哦,这是“定义”,不是推导。
- 从均匀分布$U(0,1)$采样的任意$t$,从数据集中采样的任意数据$x_0$,根据前向传播方法得到的$x_t$
负对数似然的上界
我们本身的目标是使得$p_\theta(x_0)$的分布接近$p_{data}(x_0)$
但是我们从未单独定义、训练$p_\theta(x)$这个模型
而是定义了一个$p_\theta(x_0^i\mid x_t)$,不断重复迭代,起到了$p_\theta(x)$的作用
因此我们上述内容得到的$L(\theta)$是作为模型$p_\theta(x_0^i\mid x_t)$的损失函数
我们如何保证训练出这个模型,可以使得$p_\theta(x_0)$的分布接近$p_{data}(x_0)$?
我们定义真实的似然函数是
$$ \mathcal{L}(\theta) = -\mathbb{E}_{p_{data}(x_0)}\left [\log{p_{\theta}(x_0)}\right] $$- 按照真实分布,采样数据$x_0$,得到的似然函数期望
我们需要最小化这个式子
定义前向加噪分布$q$:
$$ q(x_t\mid x_0) = \prod_{i=1}^L \left [ (1-t)\times 1(x_t^i=x_0^i) + t\times 1(x_t^i=M) \right] $$其描述了通过已知的前向过程,从$x_0$得到$x_t$的概率
$q$是我们引入的噪声分布,并非需要训练的参数模型,不使用$p$定义
由于前向过程是已知的,我们考虑使用它表示$p_\theta$
$$ p_\theta(x_0) = \sum_{x_t}p_\theta(x_0\mid x_t)p_\theta(x_t)= \sum_{x_t}p_\theta(x_0, x_t) $$原始句子出现的总概率就是把所有可能路径的概率加起来。
(先得到$x_t$,再生成$x_0$)
引入已知的$q$
$$ p_\theta(x_0) = \sum_{x_t}q(x_t\mid x_0)\frac{p_\theta(x_0,x_t)}{q(x_t\mid x_0)} $$其中$\sum_{x_t}q(x_t\mid x_0)] \times (\cdot)$,可以理解为对$q(x_t\mid x_0)$的期望
离散情况下:$\mathbb{E}_{x\sim r}(g(x)) = \sum_x r(x)g(x)$
此时$x_0$是当作固定值,所有都可以看作关于$x_t$的函数
因此则有:
$$ p_\theta(x_0) = \mathbb{E}_{ q(x_t\mid x_0)}\left[\frac{p_\theta(x_0,x_t)}{q(x_t\mid x_0)}\right] $$任意从$q$分布中采样$x_t$
采样 Jensen不等式:
$$ \log \mathbb{E}(z) \geq \mathbb{E}(\log{z}) $$此时则有:
$$ \log{p_\theta}(x_0) = \log{\mathbb{E}_{ q(x_t\mid x_0)}\left[\frac{p_\theta(x_0,x_t)}{q(x_t\mid x_0)}\right]} \geq \mathbb{E}_{ q(x_t\mid x_0)}\left[\log{p_\theta(x_0,x_t)} - \log{q(x_t\mid x_0)} \right] $$$$ -\log{p_\theta}(x_0) \leq -\mathbb{E}_{ q(x_t\mid x_0)}\log{p_\theta(x_0,x_t)} + \mathbb{E}_{ q(x_t\mid x_0)} \log{q(x_t\mid x_0)} $$分解一下联合概率
$$ \log{p_\theta(x_0,x_t)} = \log{p_\theta(x_0\mid x_t)} + \log{p_\theta(x_t)} $$代回则有:
$$ -\log{p_\theta}(x_0) \leq -\mathbb{E}_{ q(x_t\mid x_0)}\log{p_\theta(x_0\mid x_t)}-\mathbb{E}_{ q(x_t\mid x_0)}\log{p_\theta(x_t)} + \mathbb{E}_{ q(x_t\mid x_0)} \log{q(x_t\mid x_0)} $$- $p_\theta(x_t)$:其中$x_t$是前向过程人为生成的,因此与$\theta$无关
- $q(x_t\mid x_0)$是噪声项,与$\theta$无关
因此可以写成
$$ -\log{p_\theta}(x_0) \leq -\mathbb{E}_{ q(x_t\mid x_0)}\log{p_\theta(x_0\mid x_t)} + \text{const} $$两边同时对真实数据计算期望
$$ -\mathbb{E}_{p_{data}(x_0)}(\log{p_\theta}(x_0) ) \leq -\mathbb{E}_{p_{data}(x_0)}(\mathbb{E}_{ q(x_t\mid x_0)}\log{p_\theta(x_0\mid x_t)}) + \text{const} $$左边实质上就是我们需要优化的目标,命名为负对数似然$\text{NLL}$
根据
$$ \log {p_\theta(x_0\mid x_t)} = \sum_{i=1}^L 1\left [ x^i_t=M\right ] \log{p_\theta}(x_0^i\mid x_t) $$代入得:
$$ -\mathbb{E}_{p_{data}(x_0)}(\log{p_\theta}(x_0) ) \leq -\mathbb{E}_{p_{data}(x_0)}\mathbb{E}_{ q(x_t\mid x_0)}\left[\sum_{i=1}^L 1\left [ x^i_t=M\right ] \log{p_\theta}(x_0^i\mid x_t)\right] + \text{const} $$事实上右边就是:
$$ -\mathbb{E}_{p_{data}(x_0)}\mathbb{E}_{ q(x_t\mid x_0)}\left[\sum_{i=1}^L 1\left [ x^i_t=M\right ] \log{p_\theta}(x_0^i\mid x_t)\right] = -\mathbb{E}_{t,x_0,x_t}\left[\sum_{i=1}^L1\left[ x^i_t=M\right] \log{p_\theta\left( x_0^i\mid x_t\right)}\right] = tL(\theta) $$上述内容都是正项(负概率对数),$t \in [0,1]$,因此满足
$$ -\mathbb{E}_{p_{data}(x_0)}\mathbb{E}_{ q(x_t\mid x_0)}\left[\sum_{i=1}^L 1\left [ x^i_t=M\right ] \log{p_\theta}(x_0^i\mid x_t)\right] + \text{const} \leq L(\theta) + \text{const} $$则有:
$$ \text{NLL} = -\mathbb{E}_{p_{data}(x_0)}(\log{p_\theta}(x_0) ) \leq L(\theta) + \text{const} $$至此,成功证明了$L(\theta)$决定了$\text{NLL}$的上界(常数可以忽略)
Pre-Training
- 输入:
mask predictor$p_\theta$,训练数据$p_{data}$ - 输出:$p_{\theta}$(收敛)

mask predictor采用Transformer架构- 不采用
causal mask,能看见双向上下文 - 未使用KV Cache,采用标准的
Vanilla Multi-Head Attention,每个头单独一份k,q,v - Transformer架构尽量与LLaMA3对齐,从
attention和FFN两个参数大头中,选择了减少FFN的参数量,保持参数规模可以比较
- 不采用
在自回归 LLM 生成时,生成新 token 时可以复用之前的 K/V 矩阵(不用重新算整个序列的注意力)。
这是 KV cache 的意义:极大加速推理,节省显存。
但 LLaDA 每一步预测的是 全局被 mask 的位置(不是单个 token),所以每一步输入分布会变,全序列 K/V 都要重新计算 → KV cache 无法使用。
- 99%的数据固定长度4096
- 1%的数据随机采样长度
SFT
对于问答对$(p_0,r_0)$,我们不改变提问部分,只对回答部分进行掩码加噪得到$r_t$
损失函数设计为:
$$ -\mathbb{E}_{t,p_0,r_0,r_t}\left[\frac{1}{t}\sum_{i=1}^{L'}1[r^i_t = M]p_\theta(r_0^i\mid p_0,r_t)\right] $$- $r_0$的长度是天然动态的,使用
EOS填充
Inference
给定$p_0$,我们从完全掩码的$r_1$开始
设定超参数如下:
- 迭代次数(采样步骤总数):a trade off between efficency and quality
- 生成长度:实质上是一个上界
假设我们从时间$t\in(0, 1]$转移到$s\in[0,t)$,需要做的事是:
- $p_0,r_t$作为模型的输入,预测$r_0$(模型会
unmask所有被掩码的token) - 由于我们只转移到$s$,因此需要保留$sL$个掩码
- 对预测出的$r_0$,从中随机
remask$\frac{s}{t}L$个token - 得到$r_s$
- 对预测出的$r_0$,从中随机
- $s = t, r_t = r_s$重复迭代
默认将$|t-s|$是一个定值,以定长的步长进行迭代

理论上remask策略是随机的
但是论文给出了两种基于退火的remask策略
在生成过程中,需要随机性逐步递减,冻结高确定性的部分、把随机性集中在不确定区域
- low-confidence remasking:取置信度最低的$\frac{s}{t}L$个预测token进行remask
- semi-autoregressive remasking:对序列进行分块,从左到右顺序生成

Experiments
实验1 · Scalability
- 验证:LLaDA是否与自回归模型ARM具有相同的可拓展性
目的:证明论文的核心论点:
理想情况下,无限数据+无限模型容量+正确训练 ,可以收敛到真实分布
因此不管是ARM还是DLM,只要是合格的条件生成模型,都能学到真实语言分布
因此指令跟随、上下文学习并不是ARM的专利
实验设计
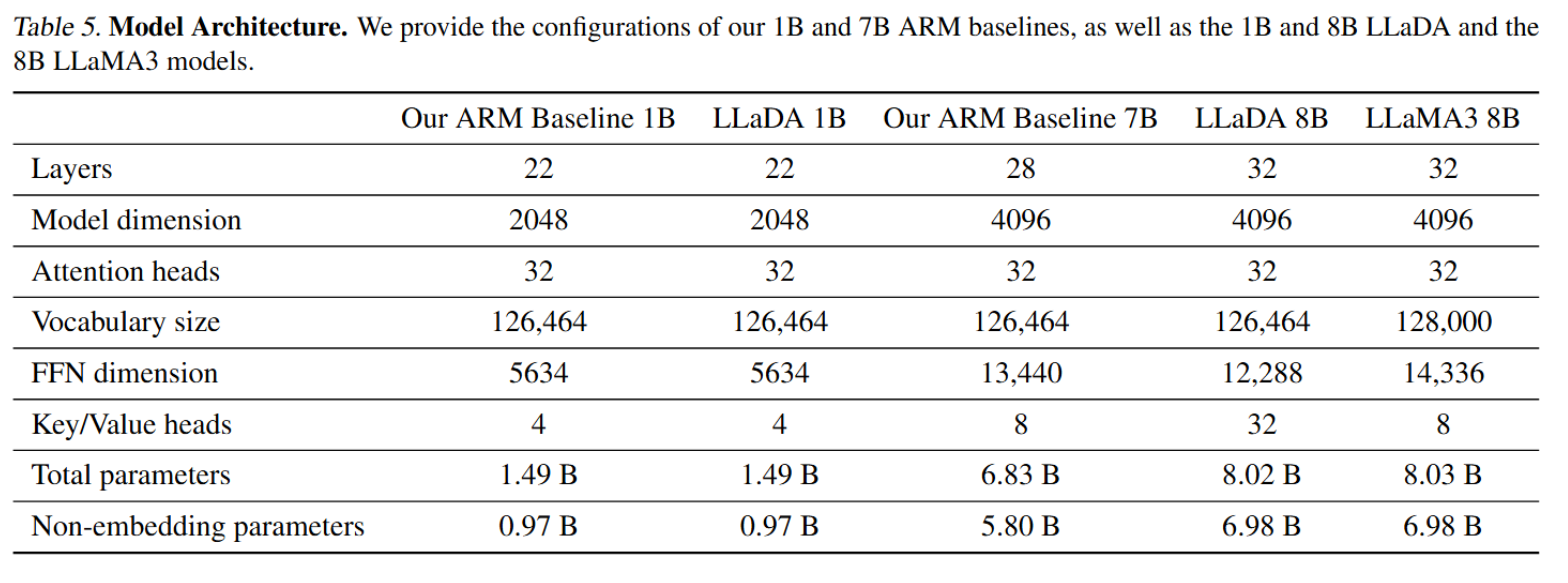
针对MDM和ARM两类语言模型,进行如下控制变量
- 模型结构:采样同一套Transformer架构(优化器、参数量……各种机制),只修改了mask
- 参数量:在1B规模下完全一致,在7B规模由于资源限制有一些不同
- Transformer:causal mask
- 数据:预训练语料相同
唯一的实验的变量:
- FLOPs:使用6ND公式作为横轴
- N 是模型的非 embedding 参数量(固定,比如 1B 或 8B)
- D 是训练过的 token 数量(数据量,可以变化)
- 实验通过改变 D ,计算出 6 × N × D (即训练 FLOPs)作为横轴的计算预算
实验指标:
- MMLU、ARC-C、CMMLU、PIQA、GSM8K、HumanEval
(多任务、推理、中文、物理、数学、代码)
实验结果
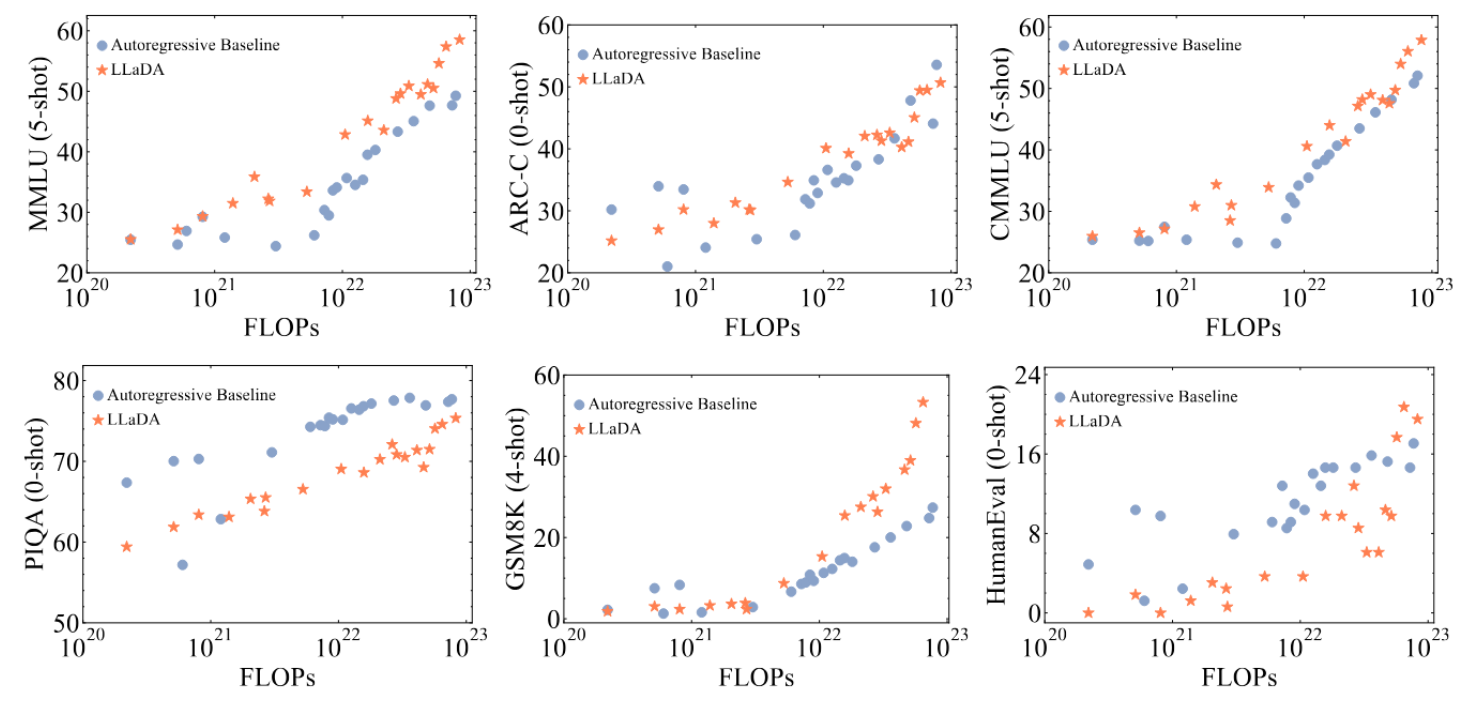
- 部分任务体现优势
- 对于性能稍逊的任务(PIQA),差距也在逐渐缩小
同时喷了先前的一篇工作的结论:达到相同的似然需要16倍算力
- 似然是间接指标(LLaDA的lower bound)
- 先前的工作只有GPT2的参数量,本文提高到7-8B
Nie, S., Zhu, F., Du, C., Pang, T., Liu, Q., Zeng, G., Lin, M., and Li, C. Scaling up masked diffusion models on text. arXiv preprint arXiv:2410.18514, 2024.
结论:LLaDA 在相同训练规模与算力条件下,表现出与 ARM 相似甚至更强的可扩展性。
实验2 · Benchmark
- 验证:LLaDA经过预训练和SFT之后是否能够和已有的ARM在上下文学习与指令遵循能力上进行竞争
实验设计
- 实验对象:LLaDA、一系列参数相当的模型
- Base阶段:比较了所有模型的预训练base模型
- instruct阶段:LLaDA只进行了SFT,其他模型均完成了SFT+RL
- 原文:交给未来的工作
- 任务:通用、数学科学、代码、中文等常见benchmark
实验结果
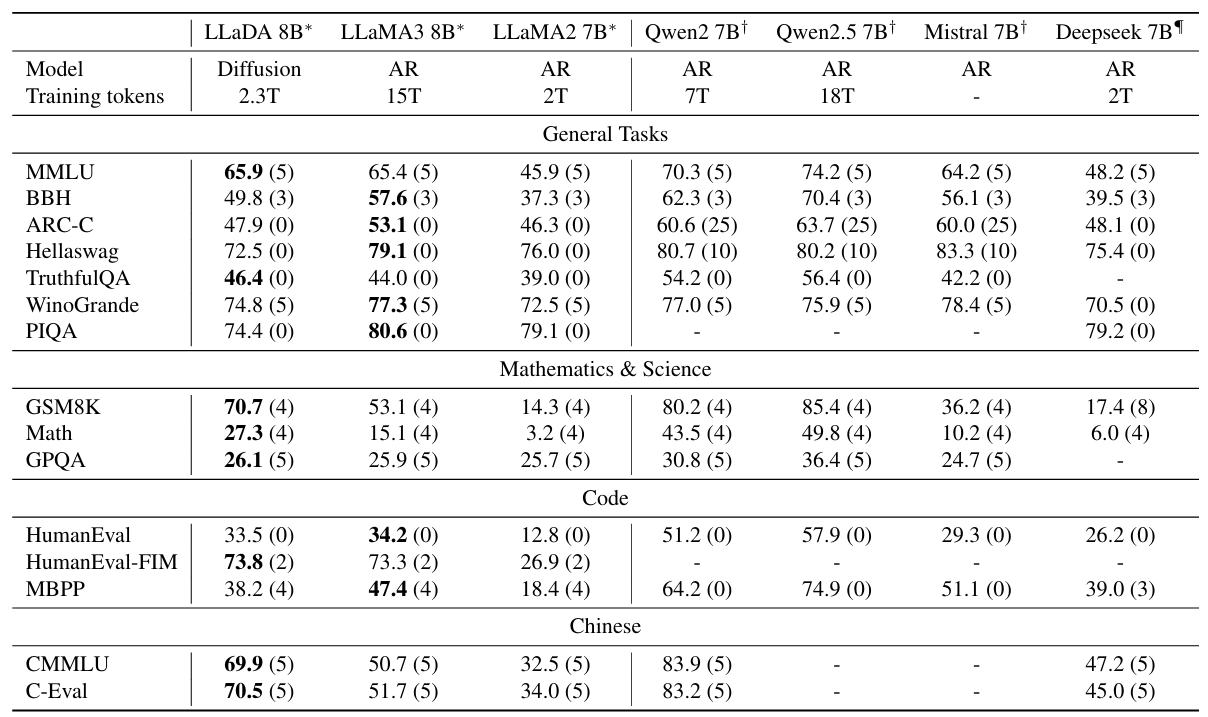
-
在所有任务上超过LLaMA2 7B,与LLaMA3 8B相当
- 所有模型的训练数据存在差异
- 作者认为LLaDA的优势区间与劣势区间的主要原因在数据质量与分布上
-
GSM8K数据集上体现了显著的优势,论文针对这个情况做了补充实验,证明不存在数据泄露
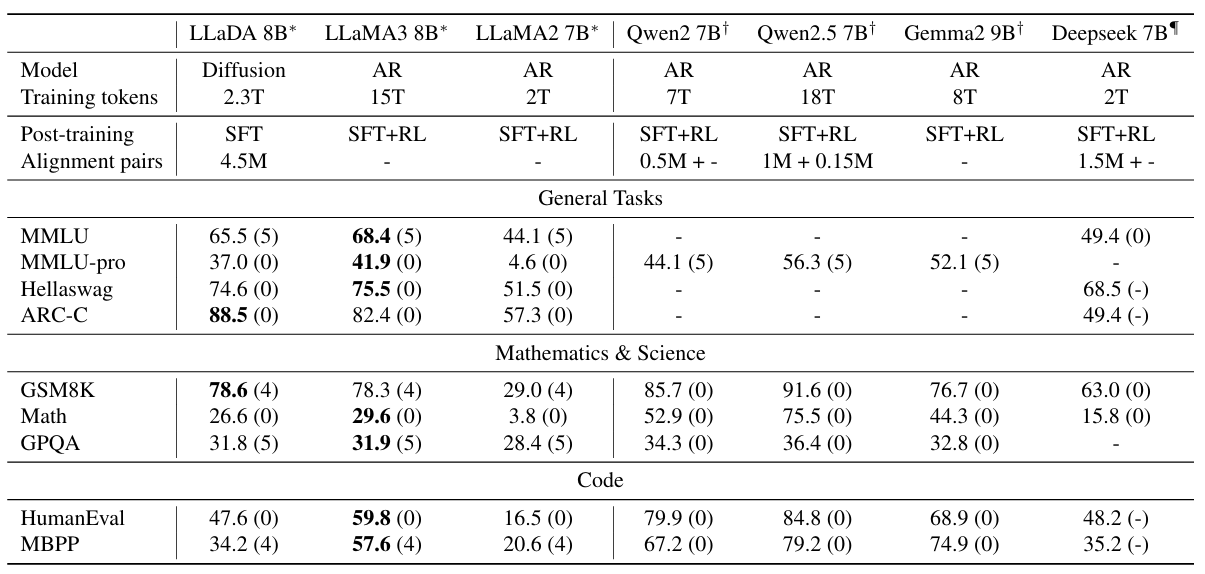
- SFT数据质量较差,出现了性能下降(MMLU)
- 没有采用RL,因此性能略微落后LLaMA3 8B
结论:
- 在数据集透明度不足的情况下,以丰富的标准化流程、多样化任务,足以证明LLaDA的性能卓越,是唯一具备竞争力的非自回归模型
实验2 · 补充实验
验证:LLaDA在GSM8K数据集中的优势不来源于数据泄露(data leakage),检测在全新数据集中仍然能保证推理能力
省流:找了一个2024年的新数据集,模仿GSM8K的形式做一遍实验

- LLaDA在所有难度(解题步骤数)中均显著优势
- 两类模型随着难度上升准确度逐渐下降,但是LLaDA下降较慢
结论:
- LLaDA允许模型在每一步同时考虑全局 token 关系,因此在多变量方程、层次关系推理中优于单向自回归
实验3 · Reversal Reasoning and Analyses
Reversal Curse(反向诅咒):ARM从左到右生成序列,因此反向生成或逆序推理的表现很差
验证:LLaDA是否克服了反向诅咒
实验设计
- 数据:496对著名中文诗句(上下两句),每一句子(A,B)构成两个任务
- Forward:给定A预测B
- Backward:给定B预测A
|
|
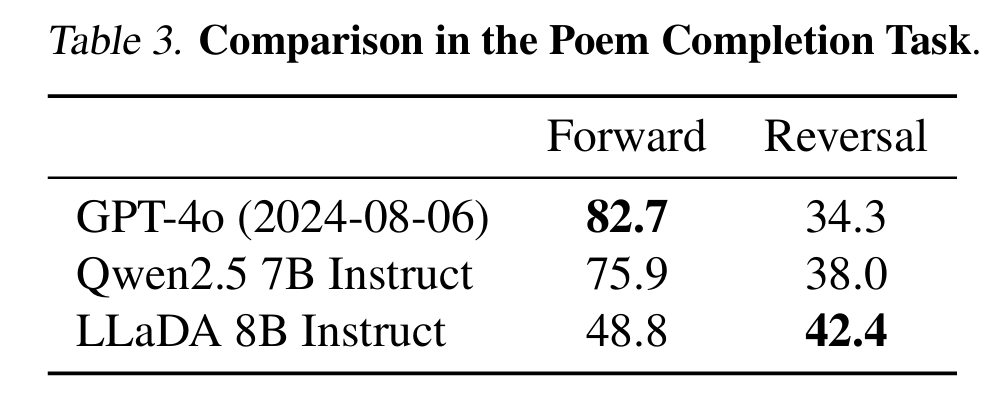
-
GPT-4o 和 Qwen2.5 均有更大数据和RL优化,但仍失败
-
LLaDA 虽仅 SFT,无RL,仍在 reversal 上大幅领先
附录补充
论文从三个角度补充了为什么LLaDA是无方向偏置的模型
- 理论证明:LLaDA本质上等价于在所有生成顺序上做平均,从而消除方向偏置
- 解释为什么 diffusion 结构在数学上是方向对称的
- 实现机制:理论正确的情况下,需要确保算法实现不出现从左到右
- 确保生成算法本身不引入方向信息
- 超参数层面:通过实验说明采样步数与效率不会干扰方向一致性
- 排除方向性差异由采样精度造成的可能性
A.2 Inference
- 目的:证明LLaDA训练和推理目标等价于对所有可能生成顺序的平均建模
对于训练时的核心目标函数:
$$ L(\theta) \triangleq -\mathbb{E}_{t,x_0,x_t}\left[\frac{1}{t}\sum_{i=1}^L1\left[ x^i_t=M\right] \log{p_\theta\left( x_0^i\mid x_t\right)}\right] $$训练目标是:模型在任意mask模式下,都能预测出原token
该训练模式不会看到任何固定方向的序列,故天然是双向建模的
推不动了,pass一下
Remasking
反向过程的核心:预测 - 重新掩码 - 继续预测
上文提到了三种不同的掩码策略
论文使用GSM8K进行了消融实验
- 生成长度固定512
- 采样步数固定256(长度的一半)
- block:32

- Base模型:最低置信度即可,半自回归是不需要的
- Instruct模型:必须是最低置信度+半自回归
- 单独最低置信度会严重降低性能
论文解释:SFT阶段引入了大量
EOS,模型一般会给EOS较大的置信度。因此推理时EOS会被大量生成,并且几乎不可能被remask(置信度非常高)因此需要引入半自回归,保证每个块内收敛出连续的内容,抑制
EOS早产
尽管引入半自回归,但是块内仍然是并行的(?)
补充一下,模型对生成长度这个超参数非常不敏感

但对采样步数非常敏感(生成长度1024)
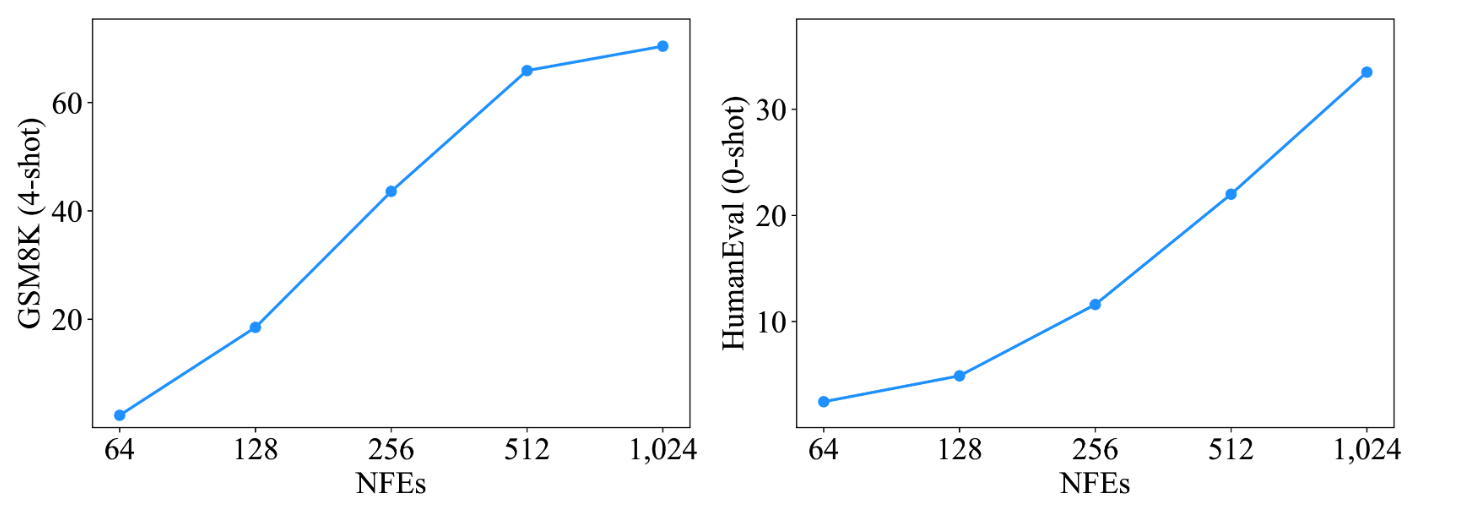
结论:
- LLaDA不受自回归方向性的约束,具有更平衡的前后向建模能力
Case Studies
附录中展示了一些其他例子,说明生成的对话是出色的(单轮、多轮)