[TOC]
【李宏毅】2025最新的Diffusion Model教程!1小时清楚扩散模型原理,简直不要太爽!人工智能|机器学习|OpenAI_哔哩哔哩_bilibili
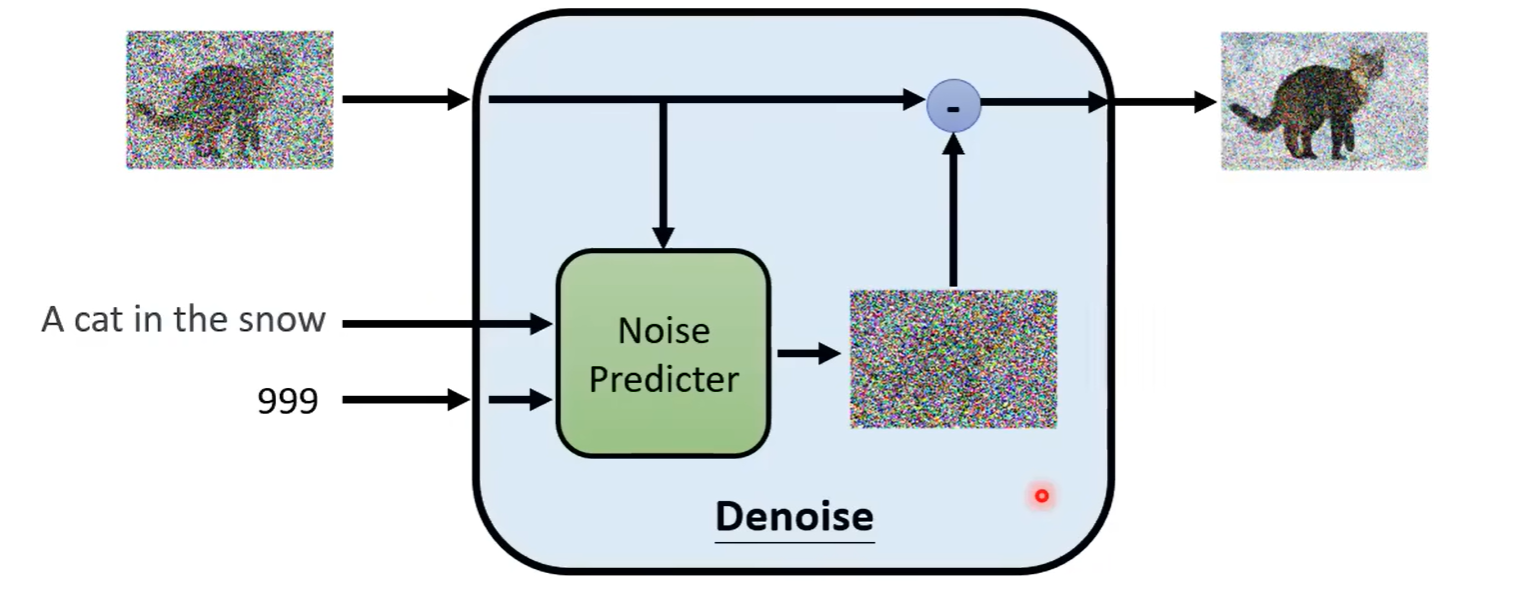
Denoise Model
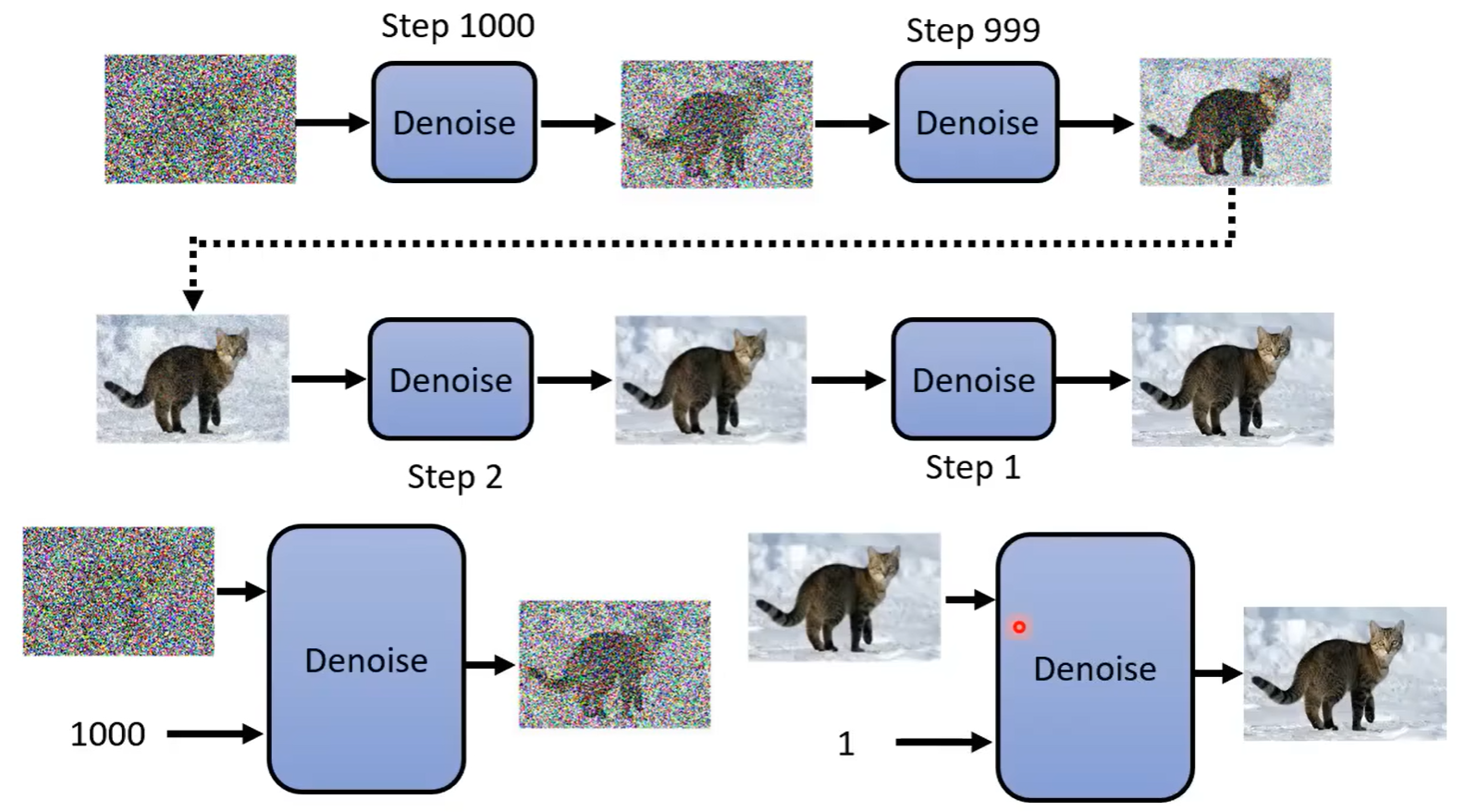
- 第一步,从正态分布中随机一个二维向量(纯噪声)作为最开始的输入
- 第二步,假设迭代次数为1000,将输入送入Denoise Model进行推理,得到新的图片
- 不断重复步骤(同时需要输入当前step数字,表示噪声的严重程度,见图片下方)
- 完成迭代,得到生成的图片
输入与输出
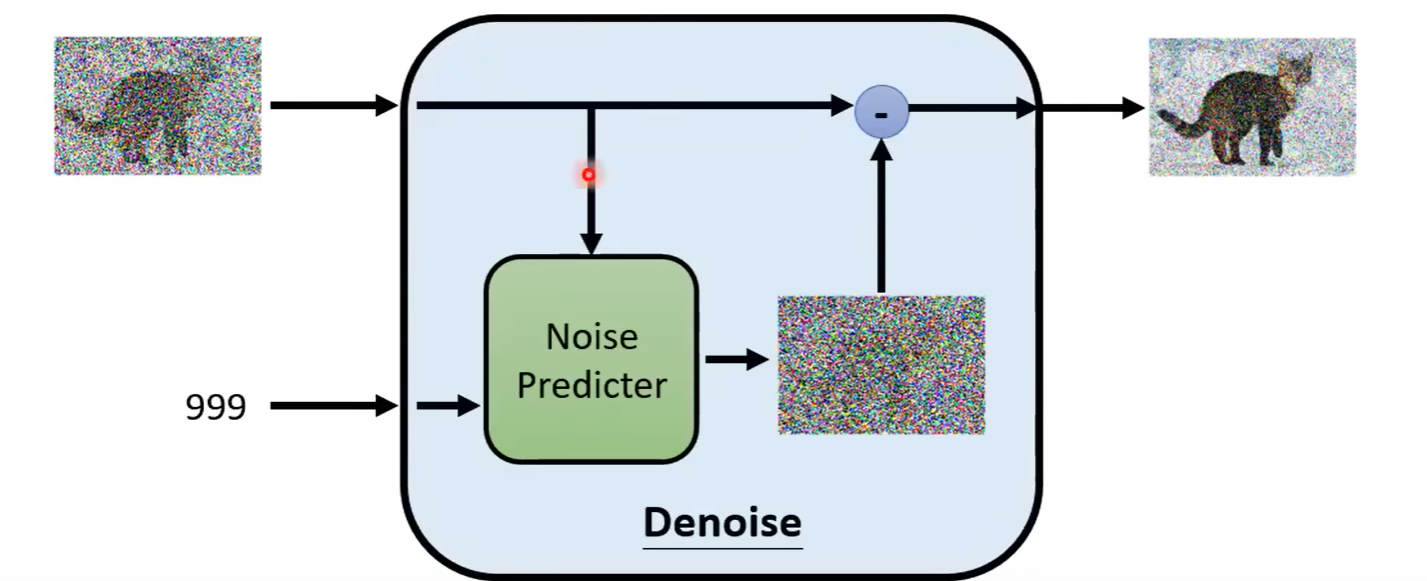
如果直接让模型输出denoise之后的图片,本质上需要让模型学会生成新的图片,实践证明是一件比较难的事情
但是我们将模型训练成一个Noise Predicter,推理出图片中的噪音是什么样的
最后使用图片减去噪音,则可以得到迭代出的图片
Train
数据可以自己造,迭代一定次数,每次生成一个正态分布随机出的噪声
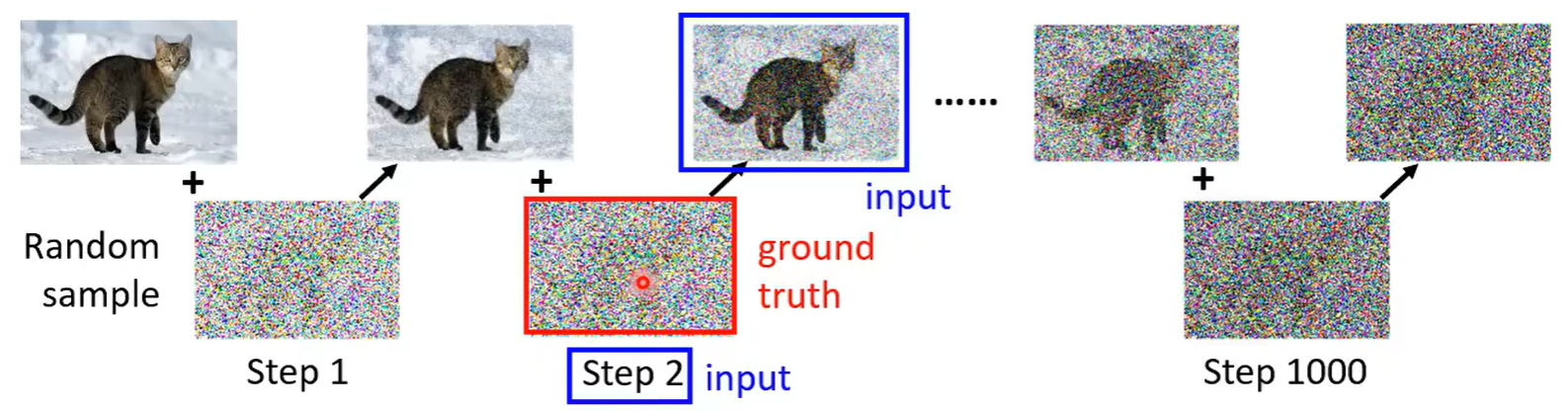
生成的噪声就是ground truth
Text2Img
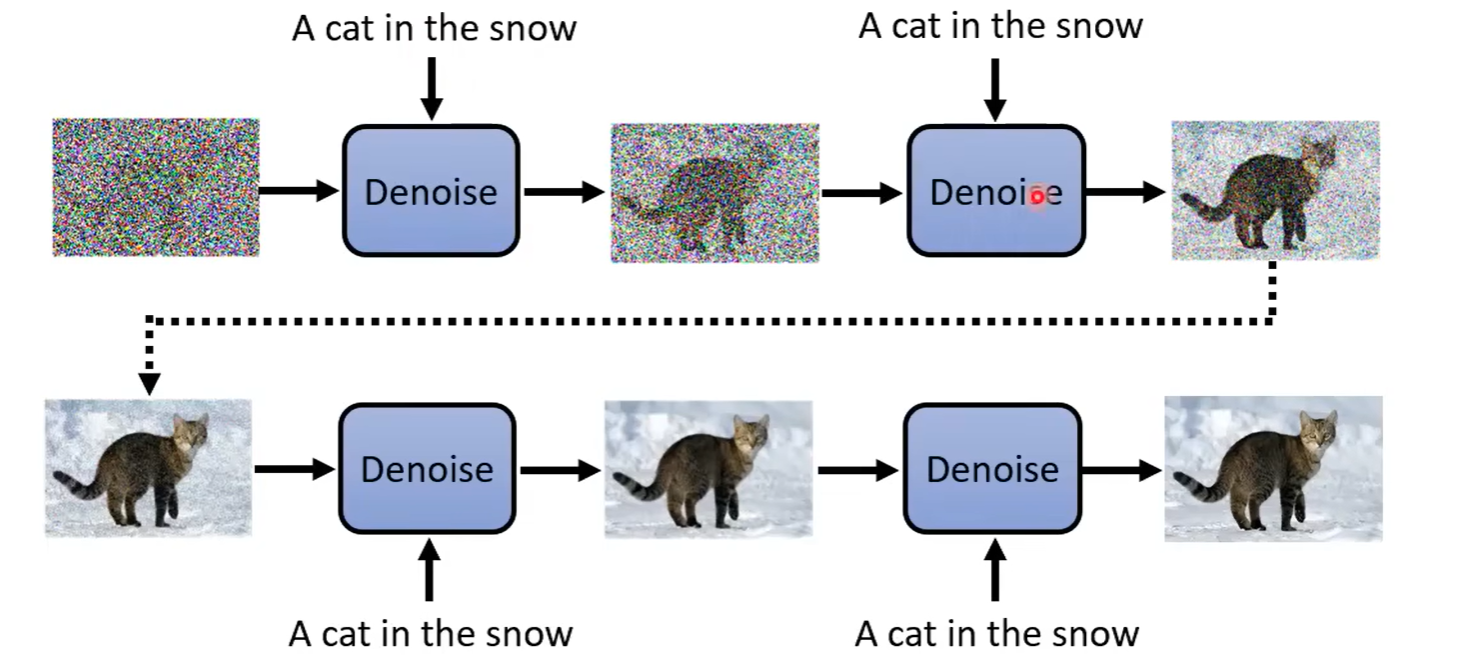
一般来说我们希望通过文字prompt生成想要的图片,而不是让模型自己决定生成什么样的图片
但其实也很简单,将文字作为输入送入到Denoise Model中即可
Diffusion图片生成
主流的图片生成模型Stable Diffusion、DALLE……的Framework基本都差不多
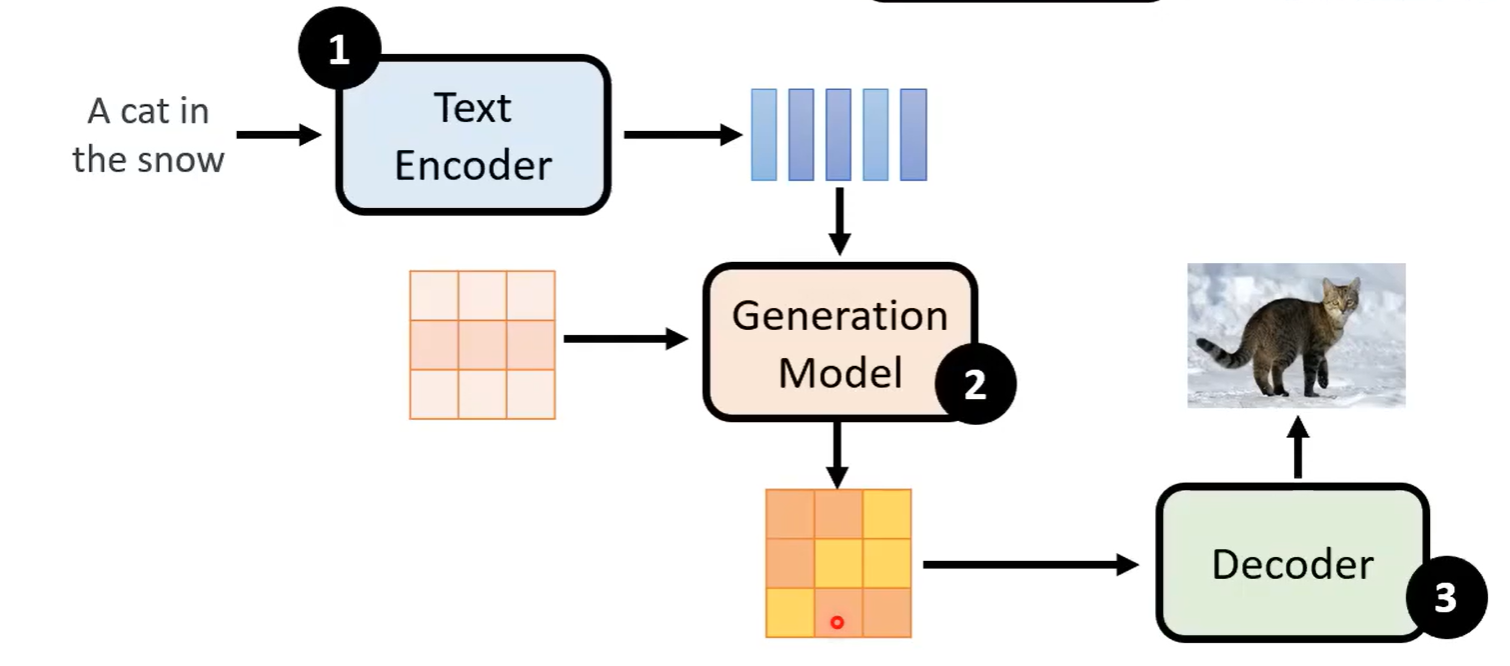
- Generation Model的输入来自于,最后输出一个类似压缩版本的图片向量
- 文字经过
text encoder得到向量 - 从正态分布中随机一个初始向量
- 文字经过
- 通过Decoder生成高清图片
Text Encoder
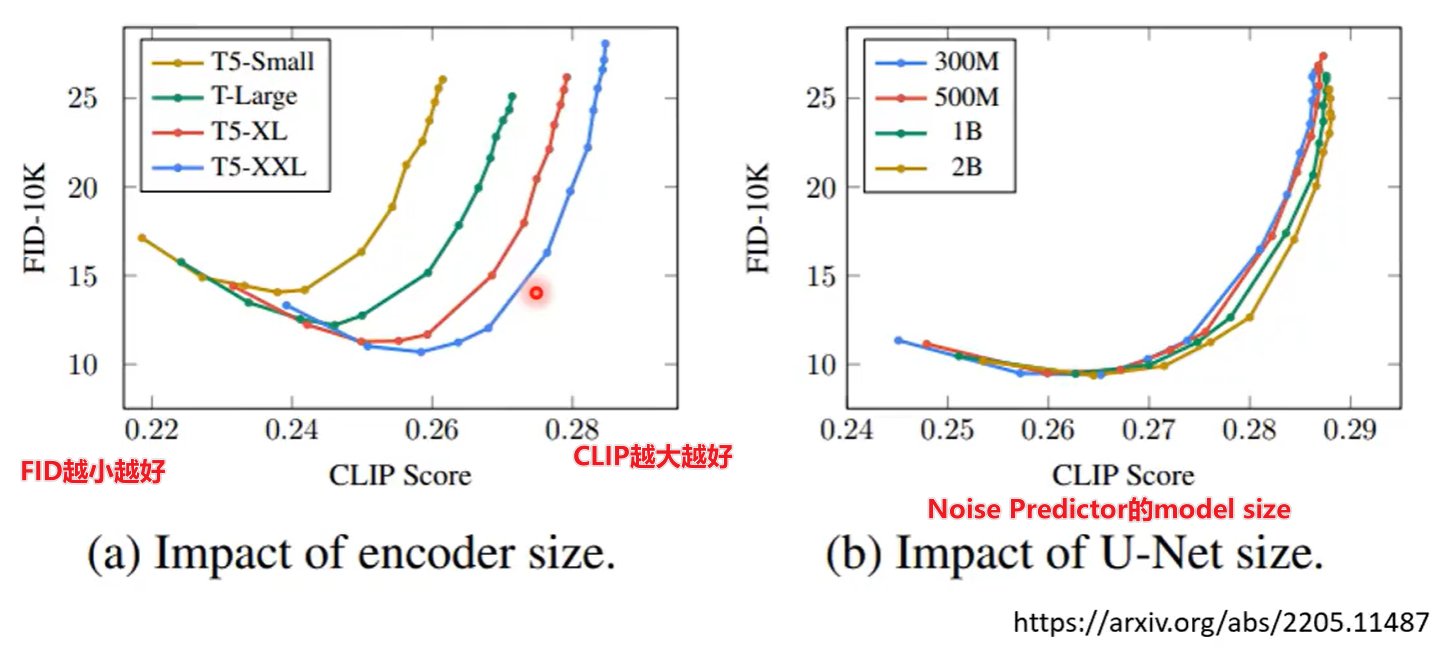
文字Encoder对最终模型的影响远大于Noise Predictor,不管采用多大的U-Net,似乎效果没什么变
Decoder
取决于Framework中的技术路线
-
Generation Model生成一张小图,Decoder进行高清图生成
- 找大量图片进行down sample,即可完成数据集制作
-
Generation Model生成Latent representation(潜在表示)
- 使用auto-encoder的方法进行训练
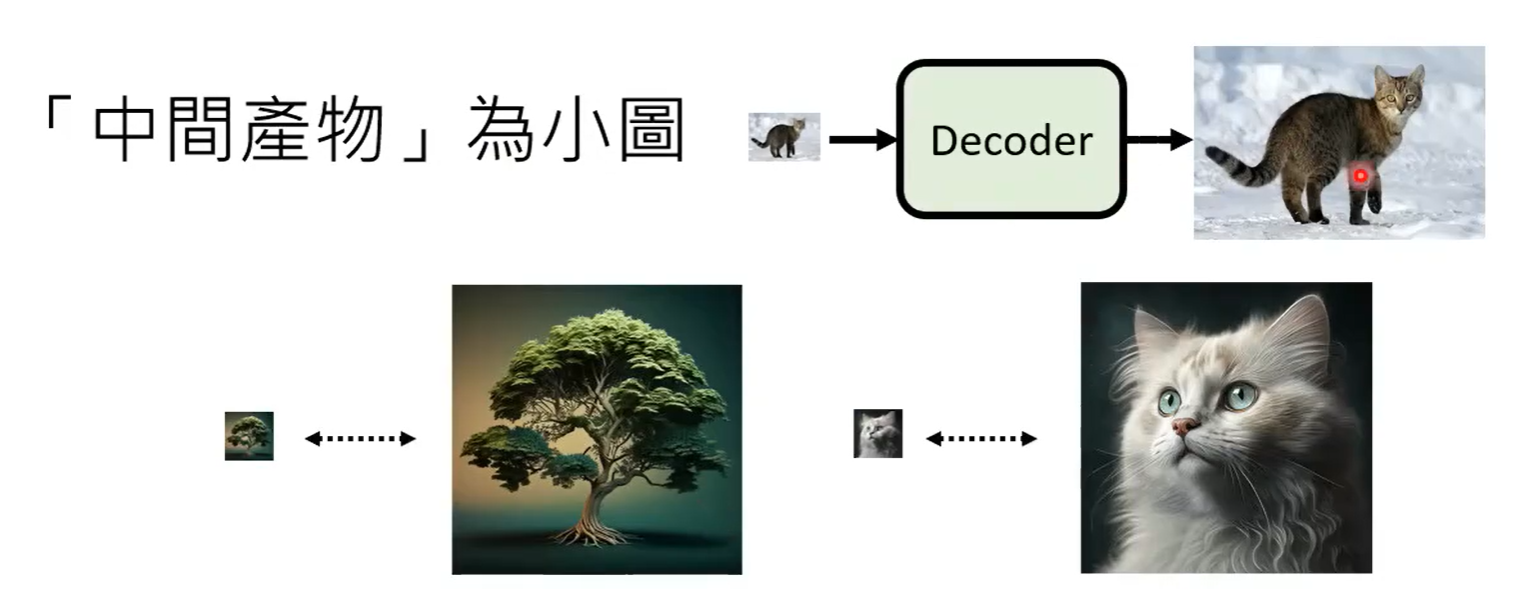
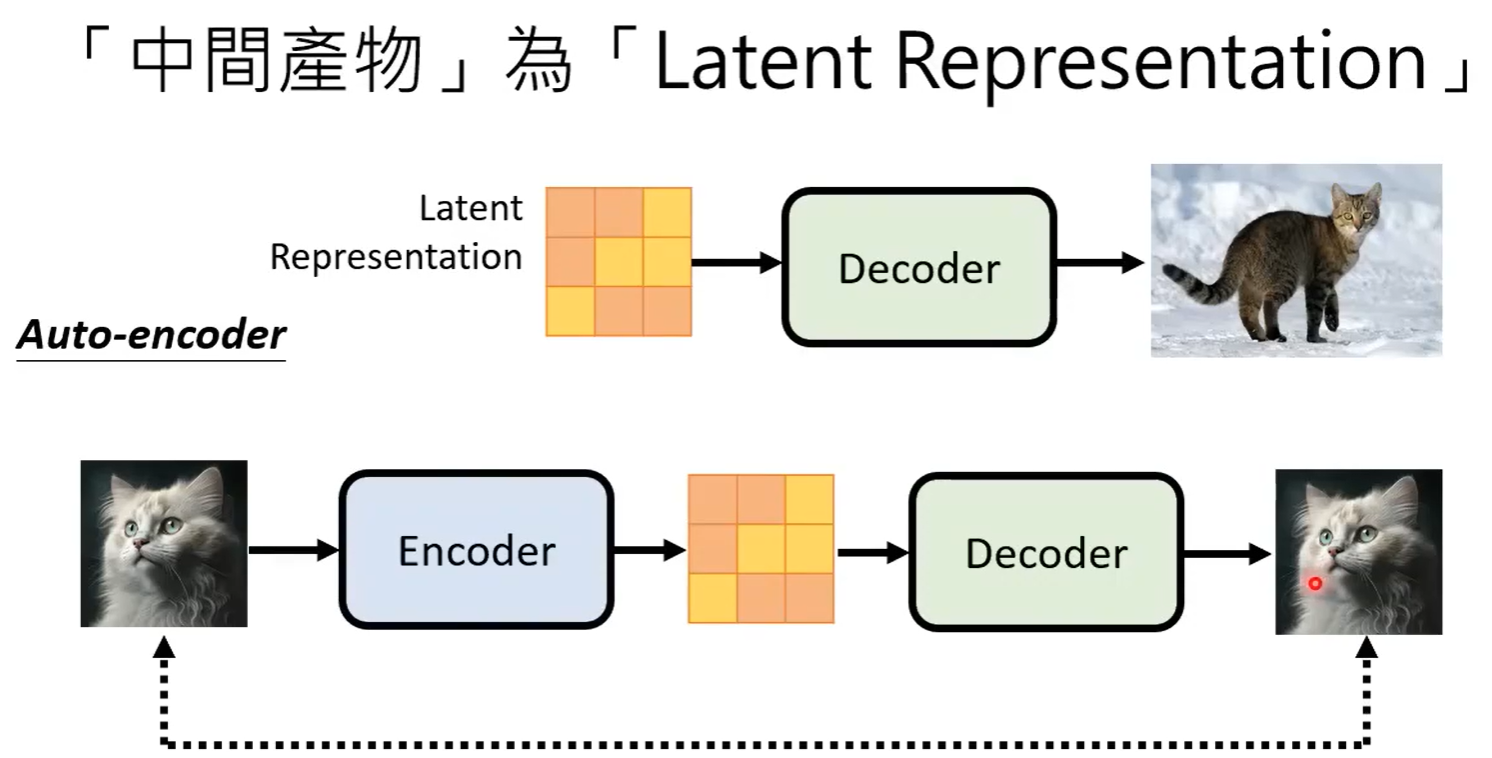
Generation Model
- Diffusion Model
- 输出:图片
- Generation Model
- 输出:Latent Representation
同样会使用Forward Process进行数据生成
因此随机的noise应该加在Latent Representation上
数学推导
优化目标
图像生成的本质:
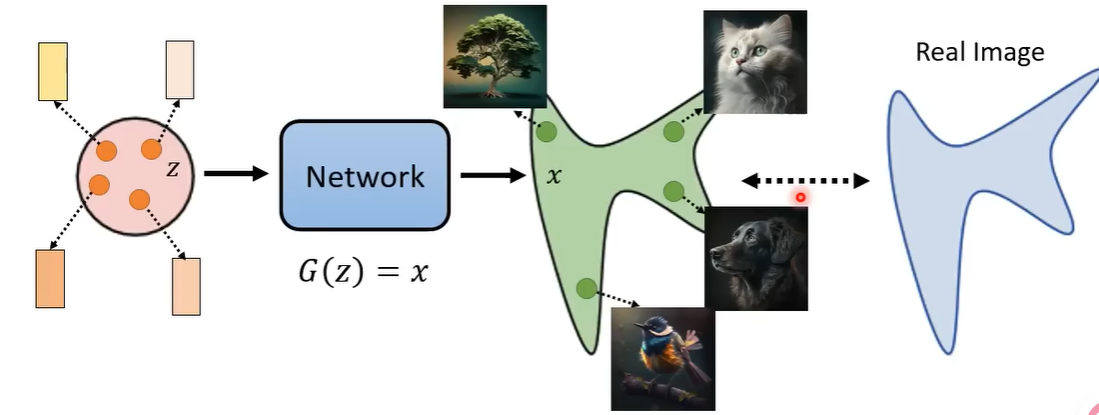
从一个高斯中随机出的向量$z$,通过生成网络$G(z)$得到的分布$x$,希望尽可能接近真实
- 文字等其他信息作为condition(本质上是条件概率)
记模型的参数为$\theta$,则模型的概率分布为$P_\theta{(x)}$,真实数据的分布为$P_{data}{(x)}$
$$ Sample \left\{ x^1, x^2, ..., x^m\right \} \space from \space P_{data}(x)\\ \theta^*=\arg \max_\theta \prod_{i=1}^{m}P_\theta{(x^i)} $$$$ \theta^*=\arg \max_\theta \sum_{i=1}^{m}\log P_\theta{(x^i)} =\arg \max_\theta \frac{1}{m}\sum_{i=1}^{m}\log P_\theta{(x^i)} $$希望模型能以尽可能高的概率生成我们观察到的数据
只要我们从真实数据中采样的数据量$m$足够大,就可以用真实数据的期望,代替样本的均值
$$ \theta^*=\arg \max_\theta \mathbb{E}_{x\sim P_{data}}\left [ \log P_\theta(x) \right] $$转换成积分形式:
$$ \theta^*=\arg \max_\theta \int P_{data}(x)\log P_\theta(x) dx $$概率乘上数值
KL散度
有两个概率分布:
- P分布:代表真实的情况或我们观察到的数据分布。
- Q分布:代表我们模型预测的分布、一个近似分布
现在的问题是:如果我们使用Q分布来编码来自P分布的数据,会犯多大的“错误”?会损失多少信息?
使用KL散度进行表示
KL散度是不对称的
- 用Q近似P的损失 不等于 用P近似Q的损失
对于离散型变量:
$$ D_{KL}(P\mid\mid Q) = \sum_i P(i)\log (\frac{P(i)}{Q(i)}) $$- $P(i)$是事件$i$在真实分布$P$中发生的概率。
- $Q(i)$是事件$i$在近似分布$Q$中发生的概率。
对于连续型变量:
$$ D_{KL}(P\mid\mid Q) = \int_{-\infty}^{\infty}p(x)\log (\frac{p(x)}{q(x)})dx $$这里使用的是概率密度函数
$$ \int P_{data}(x)\log P_\theta(x) dx = \int P_{data}(x)\log P_\theta{(x)}dx - \int P_{data}(x) \log P_{data}(x)dx + \int P_{data}(x) \log P_{data}(x)dx \\ = \int P_{data}(x)\log \frac{P_\theta(x)}{P_{data}(x)}dx + \int P_{data}(x) \log P_{data}(x)dx $$
第二项是与$\theta$无关的一项(常数),这样不影响$\theta$优化,因此可以直接舍弃
$$ \theta^* = \arg \max_\theta \int P_{data}(x)\log \frac{P_\theta(x)}{P_{data}(x)}dx\\ = \arg \max_\theta \left [ -\int P_{data}(x)\log \frac{P_{data}(x)}{P_\theta(x)}dx\right ]\\ = \arg \min_\theta \left [ \int P_{data}(x)\log \frac{P_{data}(x)}{P_\theta(x)}dx\right ]\\ = \arg \min_\theta D_{KL}(P_{data}\mid\mid P_\theta) $$Denoising Diffusion Probabilistic Models
那么如何计算$P_\theta(x)$呢?对于DDPM,图片是逐渐Denoise得到的
我们假设最后得到的干净图片是$x_0$,一开始的随机噪声是$x_T \sim \mathcal{N}(0,I)$
先补充一些数学
马尔可夫性质(离散时间)
对于一个随机过程$\left { X_t \right }_{t\in T}$,$T$是离散的时间序列$\left { 0,1,2,…\right}$
若对于任意时间点$t$,满足:
$$ P(X_t=x\mid X_{t-1}=x_{t-1},...,X_1=x_1) = P(X_t=x\mid X_{t-1}=x_{t-1}) $$也就是说,给定当前状态,未来状态与过去状态条件独立。这就是“无记忆性”。
重参数化技巧
对于深度学习过程,若途中从高斯中进行采样,是不可导的,无法进行反向传播
|
|
x的产生是随机的,无法写出关于参数的函数,无法反向传播到mu和sigma
因此我们希望引入一个具体的表达方式,方便求导
可以采用的是:
$$ x = \mu + \sigma \odot \epsilon $$其中$\epsilon \sim \mathcal{N} (0,I)$,$\odot$表示逐元素乘法,$I$是单位矩阵
|
|
我们只需要学习$\mu,\sigma$,而$\epsilon$作为随机噪声,在单次的传播过程中是固定的,不影响求导
$$ \mu = \left [\mu_1, \mu_2, ..., \mu_d\right]\\ \sigma = \left [\sigma_1, \sigma_2, ..., \sigma_d\right]\\ \epsilon = \left [\epsilon_1, \epsilon_2, ..., \epsilon_d\right],\epsilon \sim \mathcal{N}(0,1) $$因此
$$ x = \mu + \sigma \odot \epsilon\\ x_i = \mu_i + \sigma_i \cdot \epsilon_i,\forall i\\ \therefore x_i\sim \mathcal{N}(\mu_i,\sigma^2_i) $$各维度是独立的
分布
假设你想知道"今天是否下雨了"(未知事物),但你无法直接看窗外。
- 先验分布:在没有任何证据时,你根据历史数据猜测"今天下雨的概率是20%"
- 证据:你听到有人说"地上是湿的"
- 后验分布:在知道"地上是湿的"这个证据后,你更新对"今天下雨"的概率判断(比如变成70%)
正态分布(高斯分布)
- 性质1:均值与方差的线性组合
若$z = ay+b$,且$y\sim \mathcal{N}(\mu, \sigma^2)$,其他均为常数
则:
$$ z \sim \mathcal{N}(a\mu + b,a^2\sigma^2 ) $$- 性质2:独立正态分布的和
若$y_1,y_2$都是独立的正态分布变量,则他们的和$z=y_1+y_2$也是正态分布
$$ z\sim \mathcal{N}(\mu_1+\mu_2, \sigma^2_1+\sigma_2^2) $$加噪
加噪是一个正向过程
从数据集的原始图片$x_0$出发,最终需要得到$x_T \sim \mathcal{N}(0,I)$
如果每一步按照前文所说进行简单加噪
$$ x_t =x_{t-1} + \epsilon_t, \quad \epsilon_t\sim \mathcal{N}(0,\sigma^2I) $$其中$\sigma$可以让我们自己定义
故随着时间累计:
$$ x_t = x_0 + \sum_{i=1}^t\epsilon_i $$$\epsilon_i$是独立同分布的,故
$$ x_t \sim \mathcal{N}\left ( x_0, t\sigma^2I \right) $$这样无法保证最后$x^T$是一个标准正态分布
且随着$t$增加,数值的不稳定性会上升
加噪目标:
- 最终是标准正态分布的纯噪声
- 加噪可控、平滑过渡
- 数值稳定
设计:
$$ x_t = \sqrt{1-\beta_t}\cdot x_{t-1} + \sqrt{\beta_t}\cdot \epsilon_t $$其中$\beta_t$是预先设定的缩放系数,在$(0,1)$之间
从原理上能够解释为:衰减旧图片,添加新噪声
推导一下方差:
$$ \text{Var}(x_t) = \text{Var}(\sqrt{1-\beta_t}\cdot x_{t-1} + \sqrt{\beta_t}\cdot \epsilon_t)\\ = (1-\beta_t)\text{Var}(x_{t-1}) + \beta_t\text{Var}(\epsilon_t) $$如果$x_{t-1}$之前的方差都是按照某种方式保持的很好,方差为1
同时我们知道$\epsilon_t$是标准正态分布,方差也是1
$$ \text{Var}(x_t)= (1-\beta_t)\text{Var}(x_{t-1}) + \beta_t\text{Var}(\epsilon_t) = 1-\beta_t + \beta_t = 1 $$所以后续按照此方法,能够始终保持数值稳定
高效加噪
一般迭代次数还是足够多的, 如果使用循环就会很慢
我们可以对公式进行展开:
- 迭代1次
- 迭代2次
- 迭代3次
令
$$ \alpha_i = 1-\beta_i,\quad \overline{\alpha}_t = \prod_{i=1}^{t}\alpha_i $$- $x_0$的系数:$\sqrt{\overline{\alpha}_t}$
- $\epsilon_i$的系数:$\sqrt{\beta_i\prod_{j=i+1}^t \alpha_j} = \sqrt{\beta_i\cdot\frac{\overline{\alpha}_t}{\overline{\alpha}_i}}$
得:
$$ x_t = \sqrt{\overline{\alpha}_t}x_0 + \sum_{i=1}^t\sqrt{\beta_i\cdot\frac{\overline{\alpha}_t}{\overline{\alpha}_i}}\cdot \epsilon_i $$左边是定值,右边显然服从某个正态分布
并且方差完全取决于系数,令
$$ \sigma^2_t=\sum_{i=1}^t\beta_i\cdot\frac{\overline{\alpha}_t}{\overline{\alpha}_i} = \sum_{i=1}^t\beta_i\prod_{k=i+1}^t(1-\beta_k) $$此时有:$x_t\sim \mathcal{N}(0,\sigma^2_tI)$
这里有点跳跃,我们希望之间使用一个更简单的表示替换掉这个
如果我们能够找到一个方差相等的一项,就可以替换
这里智慧的假设是
$$ 1-\overline{\alpha}_t $$使用数学归纳法进行证明,当 $t=2$时:
$$ 1-\overline{\alpha}_t = 1-(1-\beta_1)(1-\beta_2) = \beta_1+\beta_2-\beta_1\beta_2\\ \sigma^2=\beta_1(1-\beta_2) + \beta_2 = \beta_1+\beta_2-\beta_1\beta_2 $$两者相等
推导两者的递推关系
前者:
$$ 1-\overline{\alpha}_t = 1 - \overline{\alpha}_{t-1}\cdot(1-\beta_t) = (1-\beta_t)(1-\overline{\alpha}_{t-1}) + \beta_t $$后者:
$$ \sigma_t^2 =\sum_{i=1}^t\beta_i\prod_{k=i+1}^t(1-\beta_k) \\ = \sum_{i=1}^{t-1}\beta_i(1-\beta_t)\prod_{k=i+1}^{t-1}(1-\beta_k) + \beta_t \\ = (1-\beta_t)\sum_{i=1}^{t-1}\beta_i\prod_{k=i+1}^{t-1}(1-\beta_k) + \beta_t \\ = (1-\beta_t)\sigma_{t-1}^2+\beta_t $$两者递推关系相同,故有:
$$ \sigma^2_t = 1-\overline{\alpha}_t $$原噪声项满足
$$ \sum_{i=1}^t\sqrt{\beta_i\cdot\frac{\overline{\alpha}_t}{\overline{\alpha}_i}}\cdot \epsilon_i \sim \mathcal{N}(0,(1-\overline{\alpha}_t)I) $$替换成满足同一个分布的噪声项
$$ \sqrt{ 1-\overline{\alpha}_t}\cdot \epsilon $$依旧可以使得$x_t \sim \mathcal{N}(0, (1-\overline{\alpha}_t)I)$
所以完全可以写成:
$$ x_t = \sqrt{\overline{\alpha}_t}x_0 +\sqrt{ 1-\overline{\alpha}_t}\cdot \epsilon, \quad \epsilon\sim\mathcal{N}(0,I) $$至此,我们可以通过该公式直接从一个干净的$x_0$得到一个加噪图片$x_t$,极大简化了训练过程
并且该式符合重参数化的
为什么上面的公式是$\epsilon$?
由于我们保证数值稳定,因此本质上是加上关于$\epsilon_i$的一个线性组合(并且线性组合系数权重始终为1),因此等价于只加上一次的标准正态分布
去噪
去噪是训练的核心步骤与目标
定义真实的逆向分布:
$$ q\left(x_{t-1}\mid x_t\right) $$由于上文所提到的运算关系,计算$q(x_t\mid x_{t-1})$是没问题的
这里我们打断一下,不妨推导一下$q(x_t\mid x_{t-1})$的分布
首先有如下关系:
$$ x_t = \sqrt{1-\beta_t}\cdot x_{t-1} + \sqrt{\beta_t}\cdot \epsilon_t $$则有(已知$x_{t-1}$的情况推$x_t$,故可以把$x_{t-1}$看作定值,且$\epsilon \sim \mathcal{N}(0,I)$):
$$ \mathbb{E}(x_t\mid x_{t-1}) = \sqrt{1-\beta_t}\mathbb{E}(x_{t-1}) + \sqrt{\beta_t}\mathbb{E}(\epsilon_t) = \sqrt{1-\beta_t}\cdot x_{t-1} \\ \text{Var}(x_t\mid x_{t-1}) = \beta_tI $$故:
$$ q(x_t\mid x_{t-1})\sim \mathcal{N}(x_t;\sqrt{1-\beta_t}\cdot x_{t-1}, \beta_tI) $$补充解释一下这个诡异的分号,其代表该分布是关于$x_t$的分布,即只有$x_t$是随机变量
??????
但是反过来计算逆向分布是一件非常难的事情
我们需要学一个模型,定义为:
$$ p_\theta\left(x_{t-1}|x_t\right) $$