LLaDA-Rec - Discrete Diffusion for Parallel Semantic ID Generation in Generative Recommendation

[TOC]

Intro

Generative recommendation基于AR LLM，面临两个问题：

unidirectional constraint：无法在建模item语义时，捕获全局依赖
error accumulation：错误累积

补充一些前置知识：

RQ-VAE（Residual Quantized Variational Autoencoder）
- 需要把Item表示成一个离散的token序列（Semantic ID），使用类LLM的生成方式进行推荐
- RQ-VAE把Item的embedding压缩成离散token
  - RA-VAE是多层级的，每一层会拟合一点，最后输出一个token序列
  - 通过控制层数，控制token序列长度

将生成式推荐运用到dLMs上也面临若干问题：

Mismatch between Residual Quantization (RQ) and Discrete Diffusion
- 多层级的方案与dlms的并行不是很契合，且dlms序列中所有token同等重要
Beam Search is Not Directly Applicable to Discrete Diffusion
- Beam Search比较适合自回归的top k，但是固定从左到右
- dlms是双向的
Differences between Language Modeling and Recommendation

Contribution

Parallel Tokenization：设计了多头VQ-VAE，将物品切分为多个子向量，每个向量并行查找独立的codebook，最终生成ID
Discrete Diffusion Training：使用两种mask机制
- User-History Mask
- Next-Item Mask
Discrete Diffusion Inference：适配了Beam Search

Preliminaries

推荐任务的问题定义：

$$ \mathcal{H} = \left [ i_1, i_2, ..., i_{n-1}\right] $$

基于用户历史的物品信息，预测下一个可能的物品$i_n$

生成式推荐将单个物品表示为定长的若干个token

$$ \mathcal{S_H} = \left[c_{1,1},...,c_{1,M},...,c_{n-1,1},...,c_{n-1,M}\right] $$

我们需要找到一个最佳的模型$\theta$，使得：

$$ \theta^* = \arg \max_\theta P_\theta(s_n\mid \mathcal{S_H}) $$

这个转化为AR LLM的建模还是非常方便的

对于dLM：

$$ P_\theta(s_n\mid \mathcal{S_H}) = \prod_{t=1}^T\prod_{m=1}^M\begin{cases} P_\theta(c_{n,m}\mid s_n^t,\mathcal{S_H}) & if \space [MASK]\ 1 & otherwise

\end{cases} $$

Method

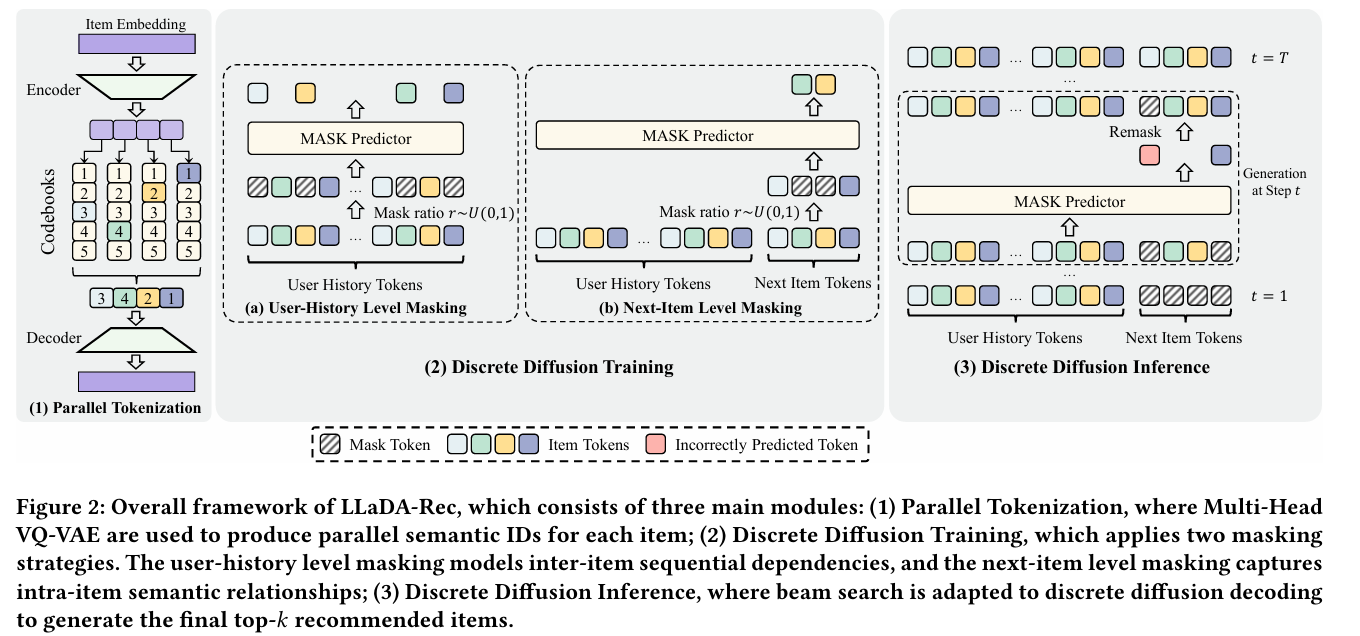
Parallel Tokenization via Multi-Head VQ-VAE

希望多个 token 之间是“完全平等”的，不应该存在 RQ-VAE 那种“前面的 token 更重要

Embedding通过Bert、Sentence-T5等得到$v_i$
通过Encoder（MLP实现），得到潜在空间$z$
将向量切成多个子向量，每个向量送入不同的Head
每个子向量查codebook，并行得到token(code index)
将code index对应的向量（code embeddings），进行拼接
Decoder重建$\hat v_i$

整个Tokenizer的损失由两部分组成：

$$ L_{Recon} = \left \| v_i-\hat v_i \right \|^2_2 $$

（L2范数的平方）

Encoder：学习如何编码到合适的latent space
Codebook：学习到如何覆盖latent space
Decoder：重建

$$ L_{VQ} = \sum_{m=1}^M \left ( \left\| sg[z_{i,m}] - e_{c_i,m}\right\|_2^2 + \alpha \left\|z_{i,m}-sg[e_{c_{i,m}}]\right\|^2_2 \right) $$

对于第一项
- sg代表阻止接受梯度，只有$e$会接受梯度
- 这样只更新codebook，使得codebook更接近latent space向量$z$（请靠近encoder的输出）
对于第二项
- sg阻止codebook的梯度
- 更新encoder，贴近codebook

最终的损失：

$$ \mathcal{L_{\text{VQ-VAE}}} = \mathcal{L_\text{Recon}} + \mathcal{L_\text{VQ}} $$

Discrete Diffusion Training

User-History Level Masking

参考LLaDA的预训练

让模型学会用户序列内部的关系

Next-Item Level Masking

参考LLaDA的SFT

理解同一 item 的 token 内部结构

但是LLaDA-Rec的训练没有分成两个阶段

提出了一个联合损失函数：

$$ L_{total} = L_{Item-Mask} + \lambda_{His-Mask}L_{His-mask} + \lambda_{Reg}\left\|\theta\right\|^2 $$

Discrete Diffusion Inference

直接使用模型不太行，没法做到生成前k个推荐项目

所以如何把Beam-Search嵌入到dlms中

一开始我们会有一个全部都是[MASK]的序列，长度为$M$：

1

[MASK] [MASK] [MASK] ... [MASK] [MASK]

dlm可以预测所有位置的生成token的置信度

假设我们要迭代$T$次，因此$K = M/T$

每次依照置信度选择前$K$个token位置，其他位置remask

根据这些位置，以及超参数$B$，迭代出$B$条置信度最高的路径

做beam search

不断迭代