[TOC]
https://www.bilibili.com/video/BV1A9tszhEpp/
不知道开了第几个坑,这里需要从头开始补一下深度学习
但是这里会比较浅,稍微过一下我忘记的知识
Pre
- 传统:专家系统、知识图谱,本质上都是设定好规则,没什么美感
- 适合已有既定规则、规律的任务(物理规则、计算)
- 机器学习:从数据中自动挖掘规律
- 难以描述的规律、规则(识别猫和狗)
- 黑盒
- 深度学习:机器学习的子集
- 更黑盒
线性代数
- 标量(scalar):年龄、身高……等单一数值
- 向量(vector)
- 物理中的意义非凡
- 机器学习中其实就是一个对象的在不同维度的属性,简称一组有序的数
区分一下向量的缩放,缩放的英语单词为scaling
线性相关
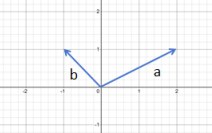
-
线性相关:如果一组向量里至少有一个向量可以表示为其他向量的线性组合,那么就称这一组向量线性相关。
-
基:向量空间的一组基是指张成该空间的一个线性无关的向量组。
线性变换
可以理解为对向量的一个函数:
- 输入:一个向量
- 输出:一个向量
但这个函数需要满足:
- 加法封闭性:$T(u+v) = T(u) + T(v)$
- 数乘封闭性:$T(cu) = cT(u)$
向量的基本操作就两个:一个是数乘,一个是向量加法
但是这样对理解来说过于复杂,不如把线性变换定义为:
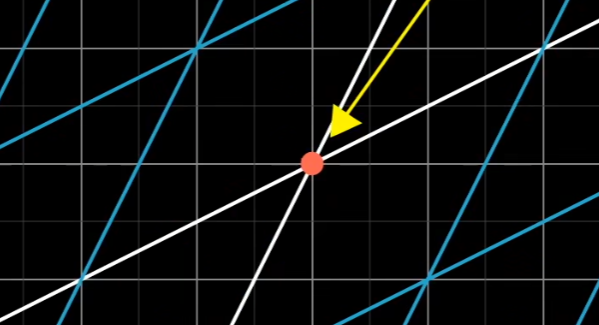
- 平面上任意直线都不会扭曲
- 原点不变
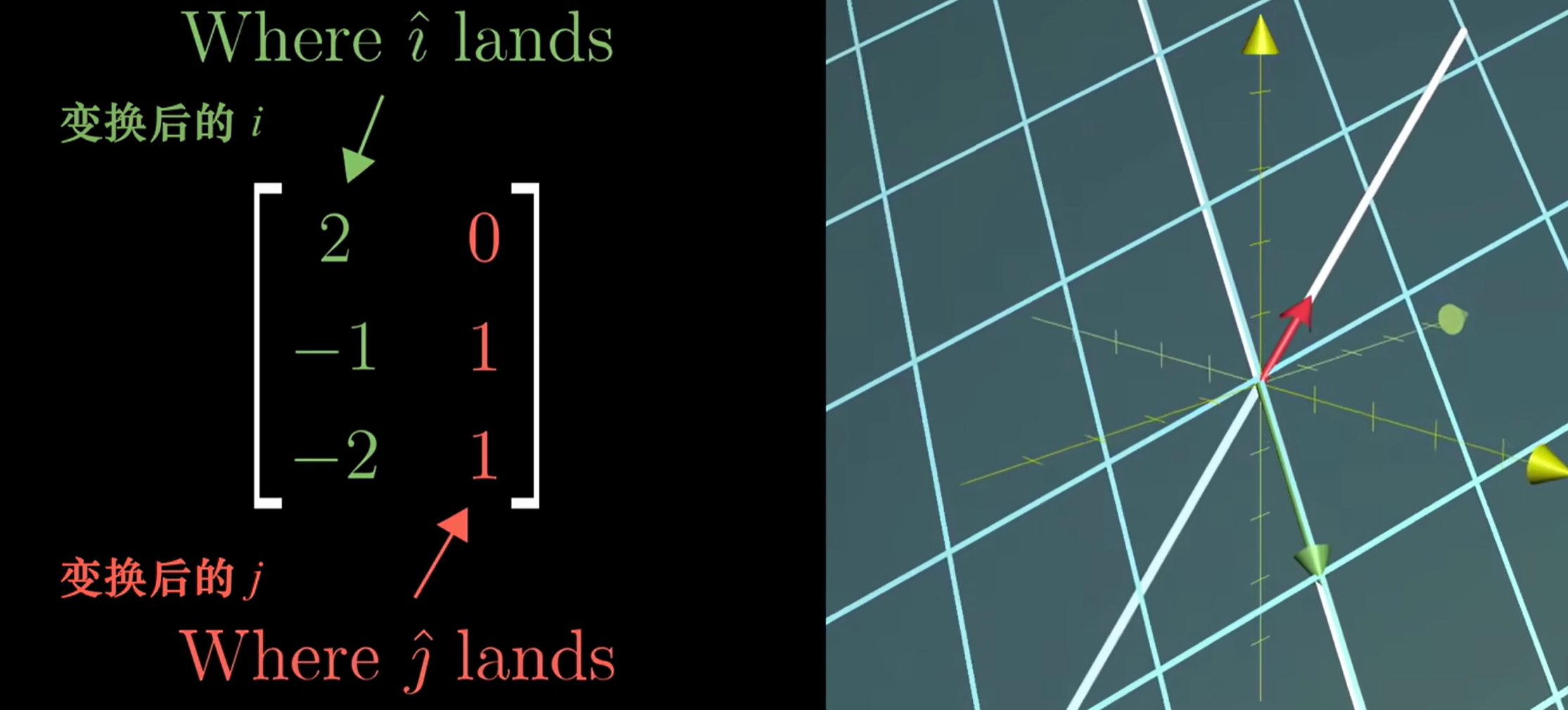
通过基向量在变换前后的变换情况,我们可以推出平面上所有向量的变换后结果:
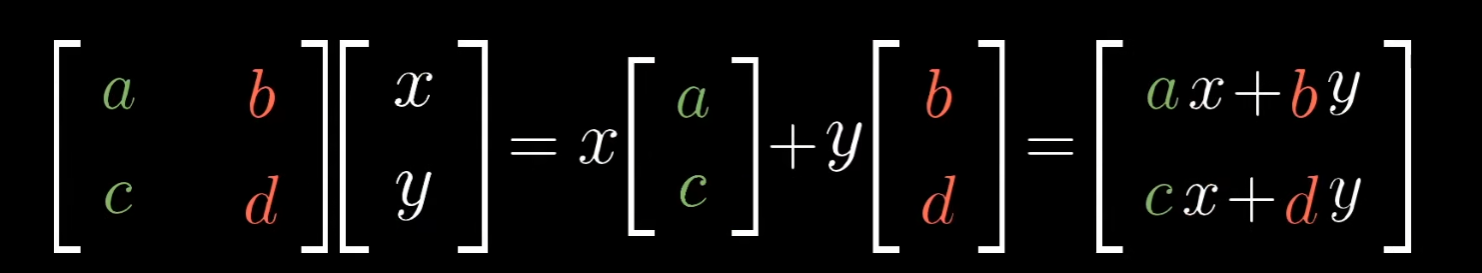
(a,c)和(b,d)就是(1,0)和(0,1)在二维平面上变换后的向量
同理,线性变换可以复合,因此可以表示为矩阵乘法:
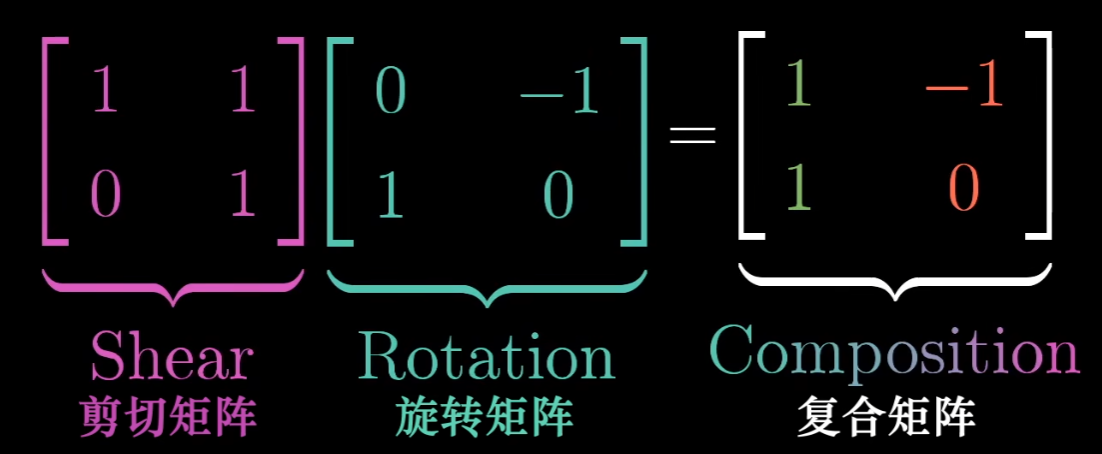
行列式
反映了线性变换对空间的**“体积”**影响
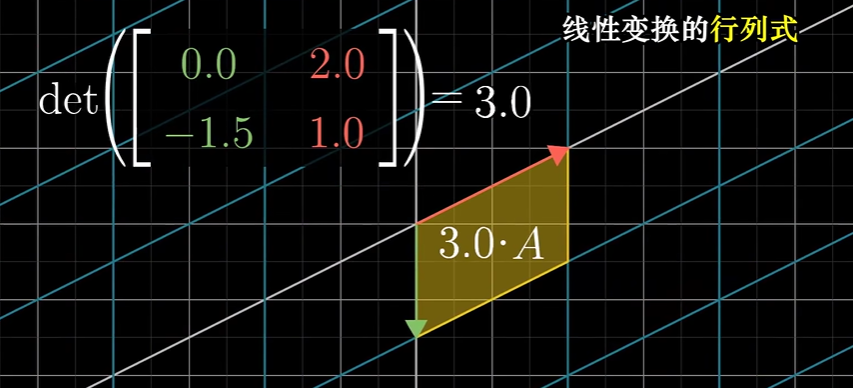
线性变换后,平面的面积会由于变换发生变换,行列式恰好反应了这一变换系数
同时面积是具有方向的(A向量到B向量之间的面积与B向量到A向量之间的面积相反)
因此行列式可以是负数
- 对于二维的线性变换矩阵,若行列式为0
- 所有向量被线性变换压缩到一条直线或点上
- 两个新的基向量是线性相关的
- 对于三维,可能被压缩到平面、直线、点中……
线性方程组
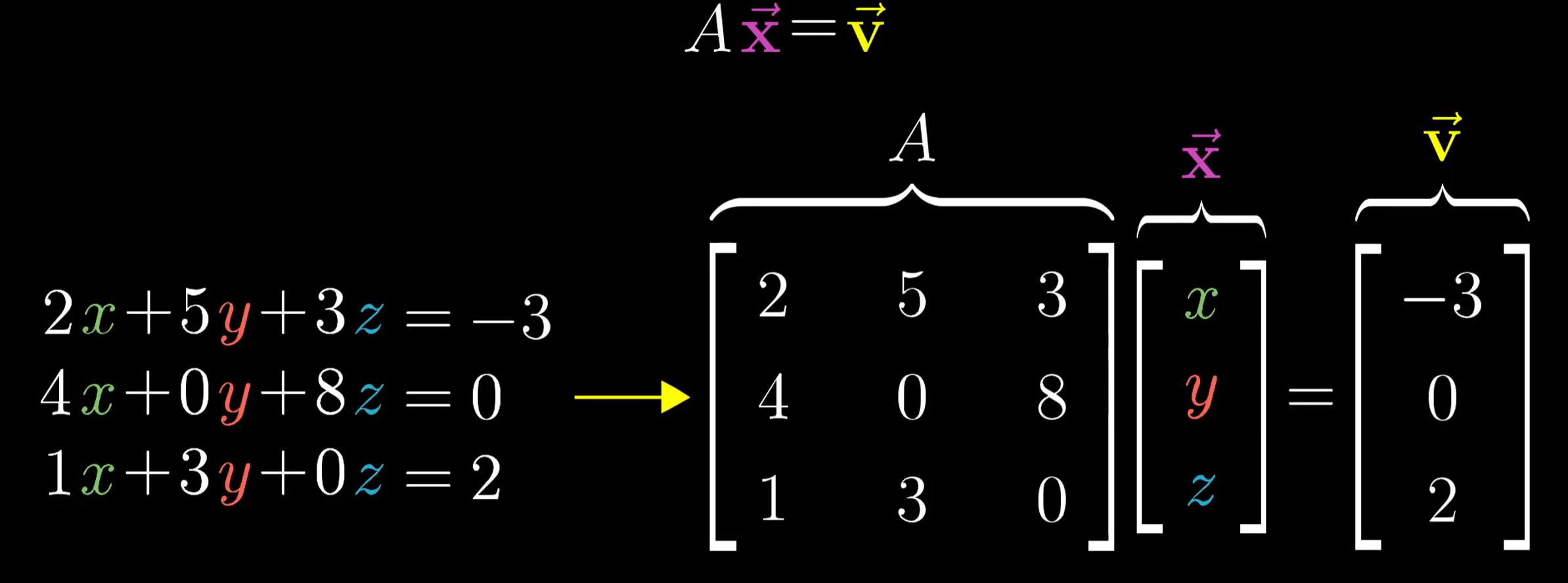
我们通过将线性方程组写成矩阵方程的形式
似乎可以表示为:求解一个向量$x$,通过线性变换$A$,与向量$v$重叠
- 当$A$的行列式不为0时
- 显然线性变化是可逆的(空间并没有被压缩)
- 因此逆矩阵是存在的,且逆矩阵可以使得$AA^{-1}$的结果为一个什么都没做的线性变换,即单位矩阵
- 所以只需要对$v$应用一个逆线性变换即可求解
- 且解唯一
- 当行列式为0,此时不存在逆矩阵(无法恢复被压缩的空间)
- 因此此时解的情况非常复杂
Rank
从线性变换后的空间出发,秩被定义为:线性变换后的空间的维数
对于线性变换矩阵$A$,其每一个列向量就是基向量的一部分
列空间
由其列向量的线性组合张成的空间即为列空间
秩就是列空间的维数
零空间
线性变换后落在零点的向量,构成零空间,或者核
$$ Ax = 0 $$非方阵
- $n\times m$维的矩阵,表示$m$维空间转化到$n$维的一个线性变换
点积

同样从几何意义出发,两个向量的点积,象征了一个向量在另一个向量的投影与该向量长度的乘积
通过这一层意义,我们可以知道点积的正、负、零的关系所带来的一些意义
但是为什么点积的计算是符合这个几何意义的?

两个列向量的点积,其实可以看做一个向量基于一个线性变换,最终被压缩到了一个一维空间
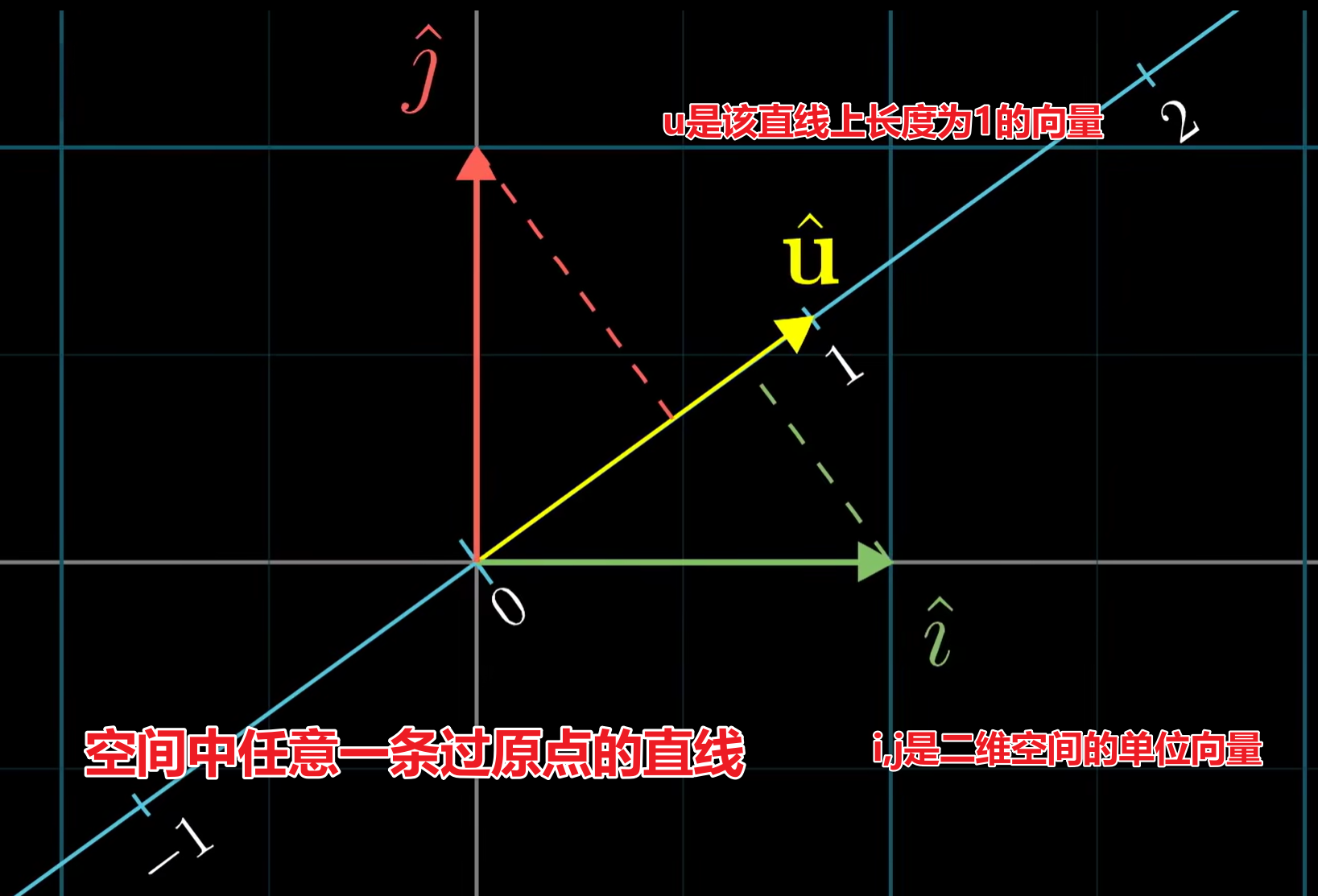
我们可以构造任意一条过原点的向量,且引入一个二维向量$u$,长度为1,恰好在这条直线的刻度1上
我们可以把空间中所有点都线性变换到这个直线所在的一维空间
显然这个过程可以使用一个$1\times 2$矩阵表示
因此我们只需要求解$i,j$变换后在直线上的刻度值,即可得到这个矩阵
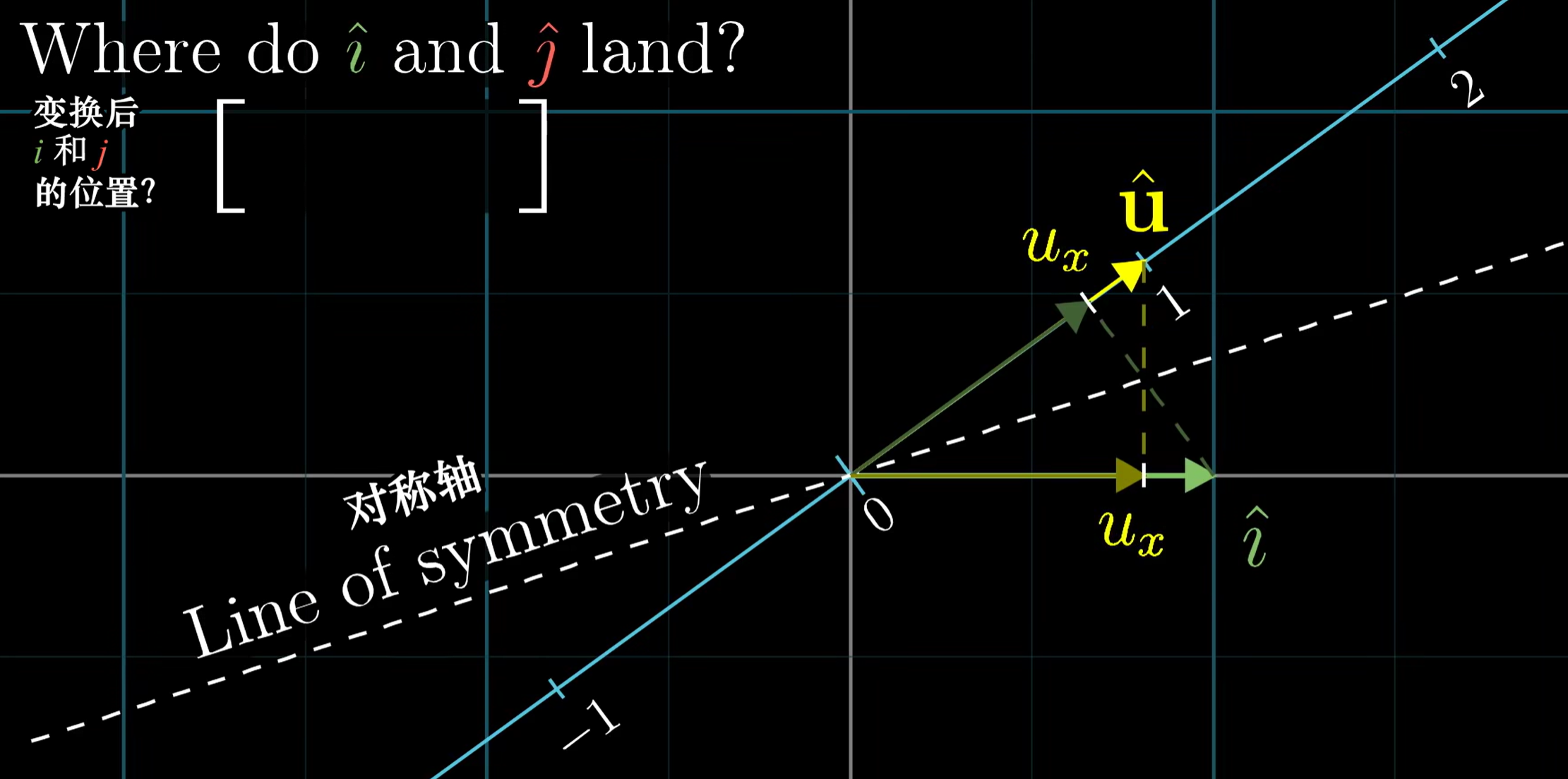
由于$i,j,u$的长度都是相同的(都是1),因此实质上具备对称性:
- $i$线性变换后的刻度值 = $u$投影到$i$的长度 = $u_x$
- $j$线性变换后的刻度值 = $u$投影到$j$的长度 = $u_y$
因此任意向量在指定单位向量上的投影值,可以表示为与这个单位向量的点积
对于非单位向量,似乎只是$u_x,u_y$乘上了一个长度系数
对于点积的结果,正是投影长度乘以这个长度系数