[TOC]
https://www.bilibili.com/video/BV1A9tszhEpp/
不知道开了第几个坑,这里需要从头开始补一下深度学习
但是这里会比较浅,稍微过一下我忘记的知识
Pre
- 传统:专家系统、知识图谱,本质上都是设定好规则,没什么美感
- 适合已有既定规则、规律的任务(物理规则、计算)
- 机器学习:从数据中自动挖掘规律
- 难以描述的规律、规则(识别猫和狗)
- 黑盒
- 深度学习:机器学习的子集
- 更黑盒
线性代数
- 标量(scalar):年龄、身高……等单一数值
- 向量(vector)
- 物理中的意义非凡
- 机器学习中其实就是一个对象的在不同维度的属性,简称一组有序的数
区分一下向量的缩放,缩放的英语单词为scaling
线性相关
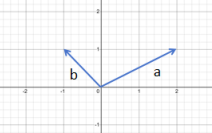
-
线性相关:如果一组向量里至少有一个向量可以表示为其他向量的线性组合,那么就称这一组向量线性相关。
-
基:向量空间的一组基是指张成该空间的一个线性无关的向量组。
线性变换
可以理解为对向量的一个函数:
- 输入:一个向量
- 输出:一个向量
但这个函数需要满足:
- 加法封闭性:$T(u+v) = T(u) + T(v)$
- 数乘封闭性:$T(cu) = cT(u)$
向量的基本操作就两个:一个是数乘,一个是向量加法
但是这样对理解来说过于复杂,不如把线性变换定义为:
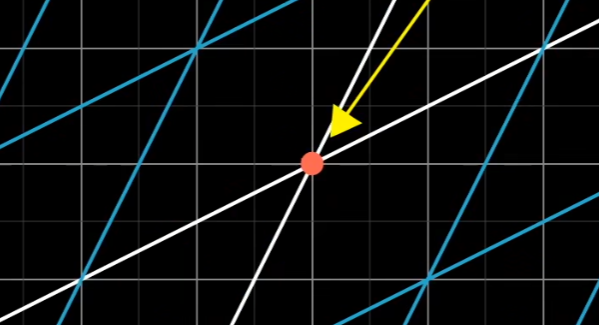
- 平面上任意直线都不会扭曲
- 原点不变
通过基向量在变换前后的变换情况,我们可以推出平面上所有向量的变换后结果:
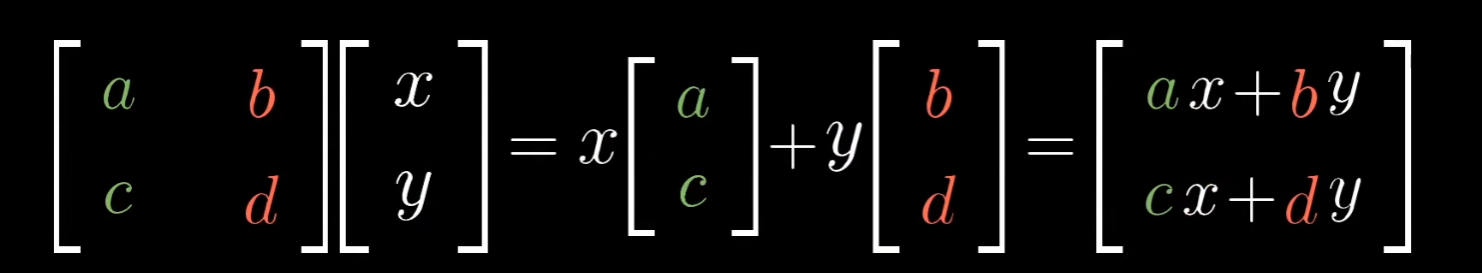
(a,c)和(b,d)就是(1,0)和(0,1)在二维平面上变换后的向量
同理,线性变换可以复合,因此可以表示为矩阵乘法:
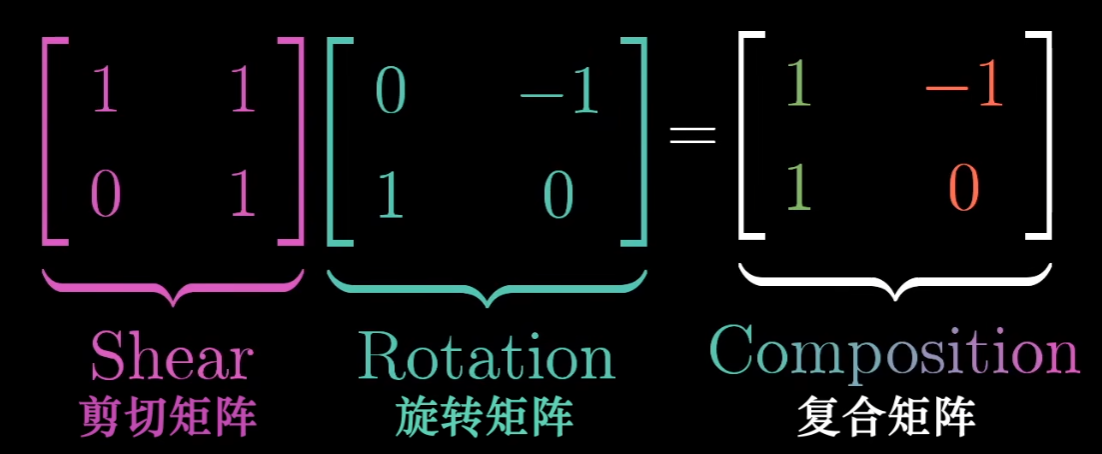
行列式
反映了线性变换对空间的**“体积”**影响
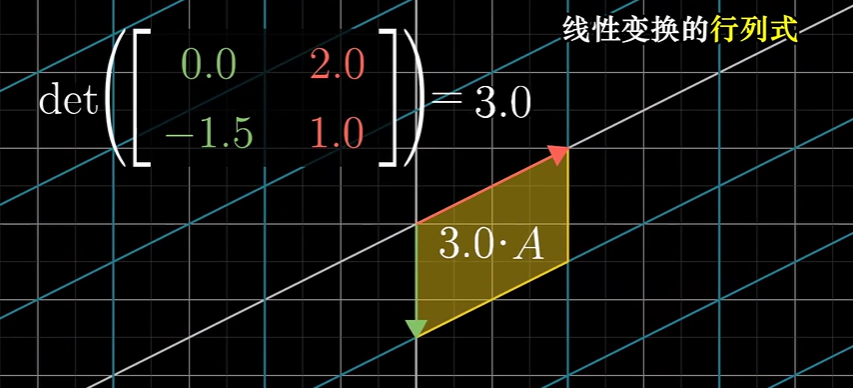
线性变换后,平面的面积会由于变换发生变换,行列式恰好反应了这一变换系数
同时面积是具有方向的(A向量到B向量之间的面积与B向量到A向量之间的面积相反)
因此行列式可以是负数
- 对于二维的线性变换矩阵,若行列式为0
- 所有向量被线性变换压缩到一条直线或点上
- 两个新的基向量是线性相关的
- 对于三维,可能被压缩到平面、直线、点中……
线性方程组
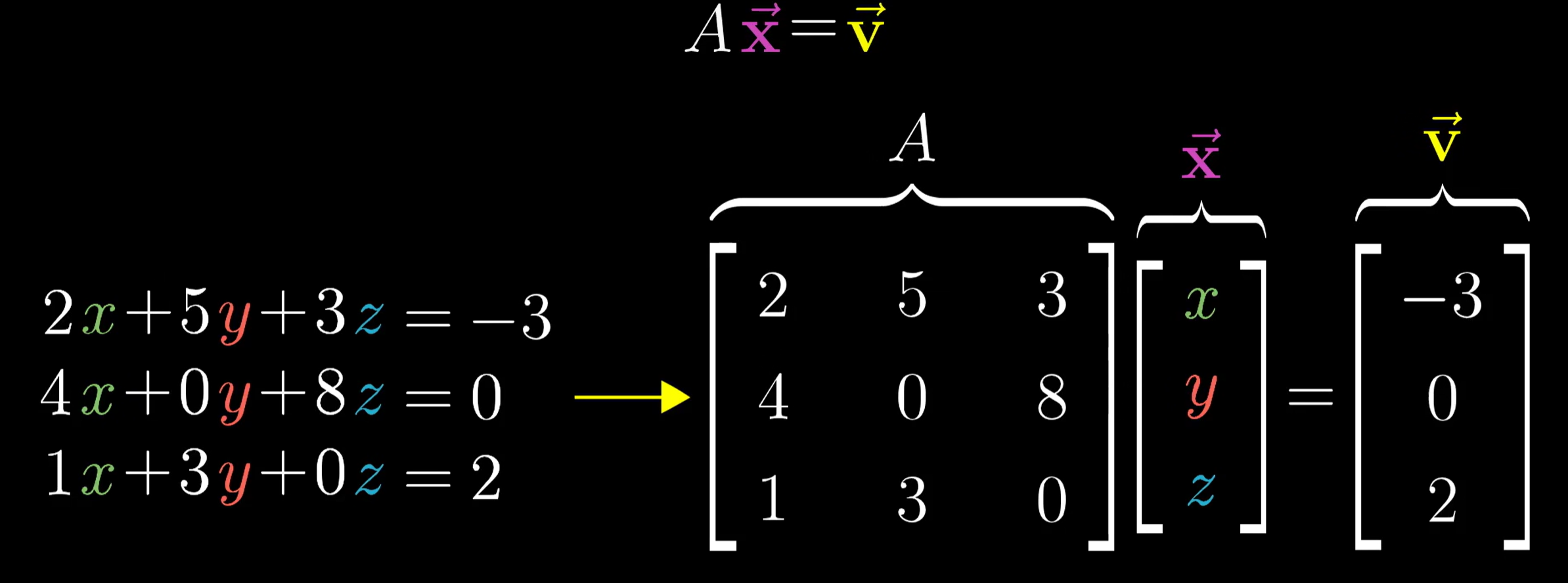
我们通过将线性方程组写成矩阵方程的形式
似乎可以表示为:求解一个向量$x$,通过线性变换$A$,与向量$v$重叠
- 当$A$的行列式不为0时
- 显然线性变化是可逆的(空间并没有被压缩)
- 因此逆矩阵是存在的,且逆矩阵可以使得$AA^{-1}$的结果为一个什么都没做的线性变换,即单位矩阵
- 所以只需要对$v$应用一个逆线性变换即可求解
- 且解唯一
- 当行列式为0,此时不存在逆矩阵(无法恢复被压缩的空间)
- 因此此时解的情况非常复杂
Rank
从线性变换后的空间出发,秩被定义为:线性变换后的空间的维数
对于线性变换矩阵$A$,其每一个列向量就是基向量的一部分
列空间
由其列向量的线性组合张成的空间即为列空间
秩就是列空间的维数
零空间
线性变换后落在零点的向量,构成零空间,或者核
$$ Ax = 0 $$非方阵
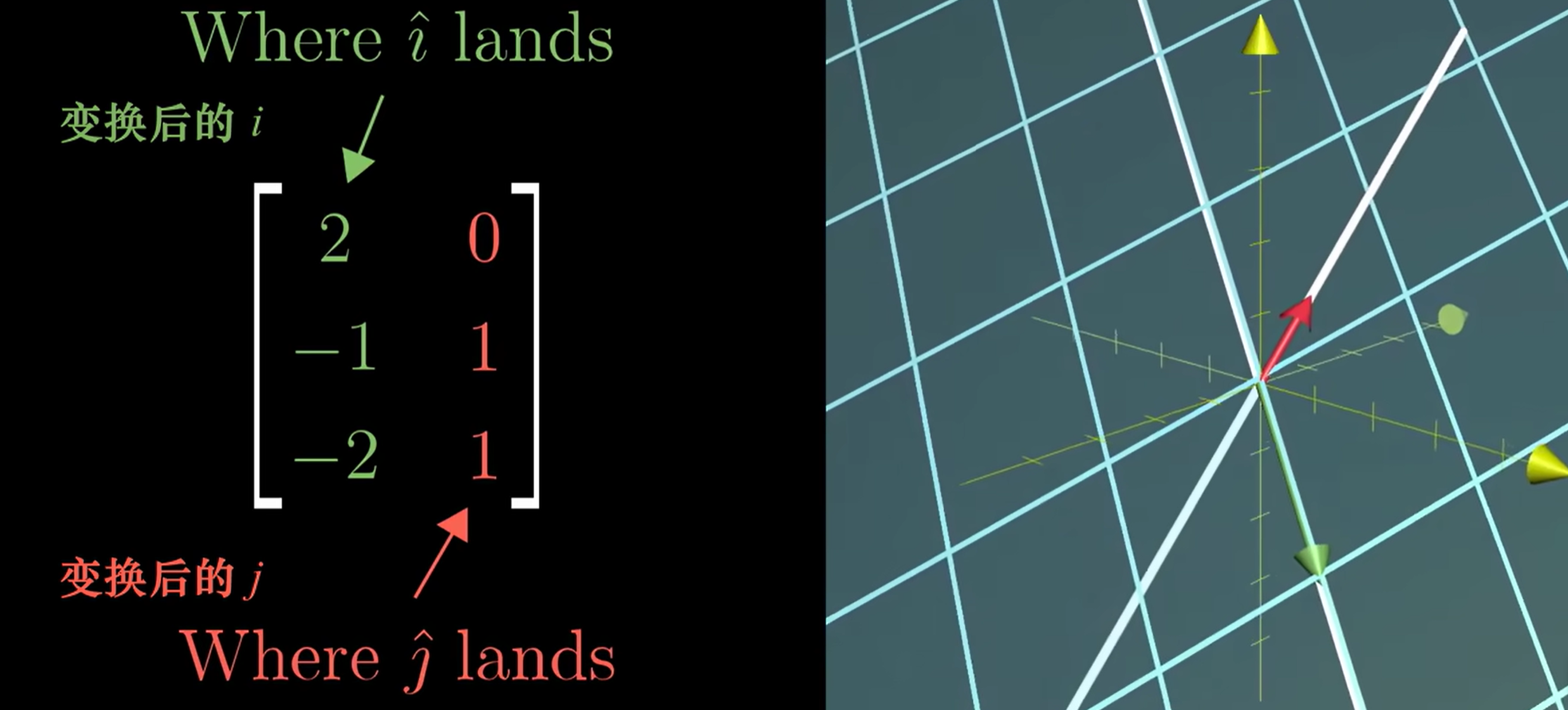
- $n\times m$维的矩阵,表示$m$维空间转化到$n$维的一个线性变换
点积

同样从几何意义出发,两个向量的点积,象征了一个向量在另一个向量的投影与该向量长度的乘积
通过这一层意义,我们可以知道点积的正、负、零的关系所带来的一些意义
但是为什么点积的计算是符合这个几何意义的?

两个列向量的点积,其实可以看做一个向量基于一个线性变换,最终被压缩到了一个一维空间
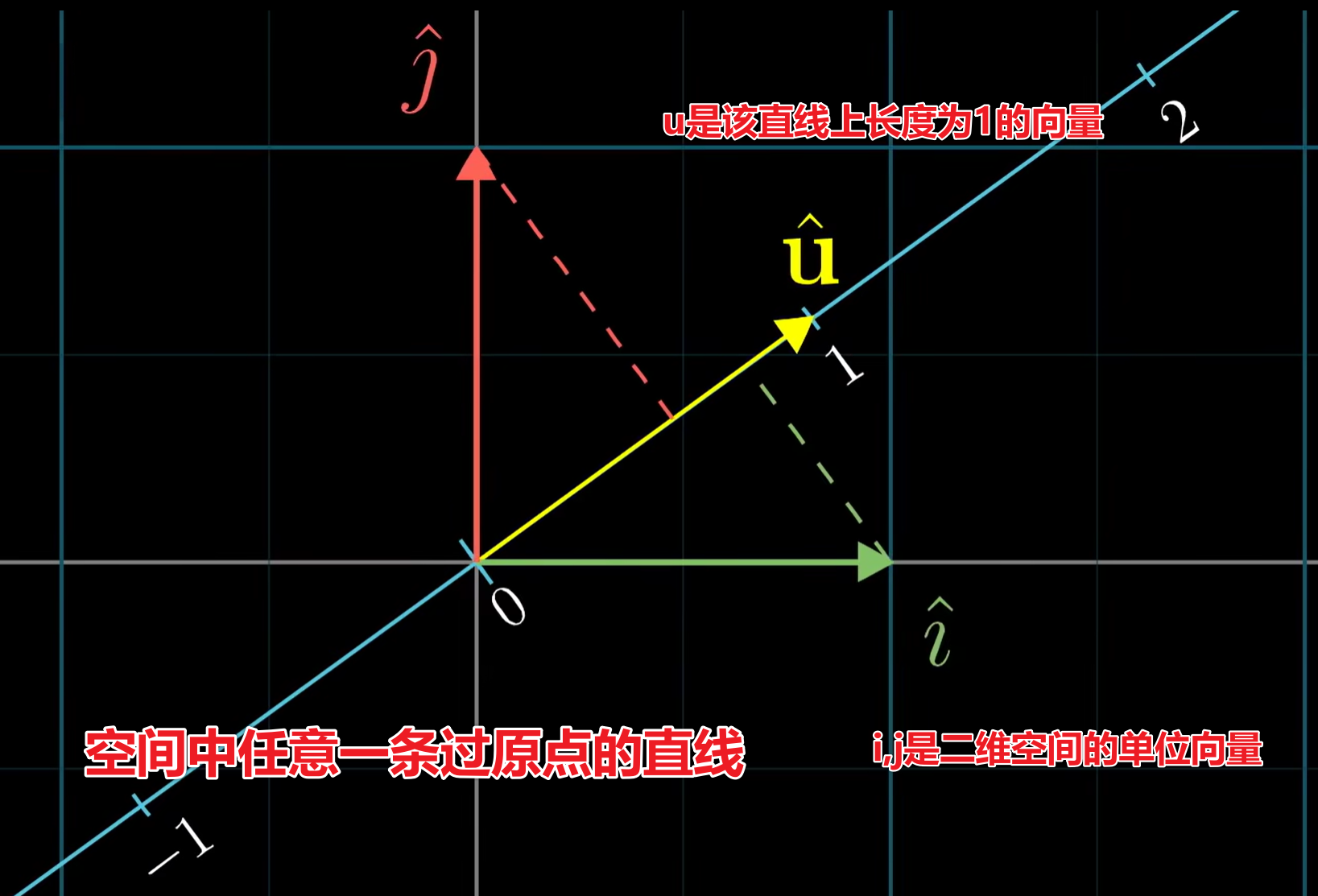
我们可以构造任意一条过原点的向量,且引入一个二维向量$u$,长度为1,恰好在这条直线的刻度1上
我们可以把空间中所有点都线性变换到这个直线所在的一维空间
显然这个过程可以使用一个$1\times 2$矩阵表示
因此我们只需要求解$i,j$变换后在直线上的刻度值,即可得到这个矩阵
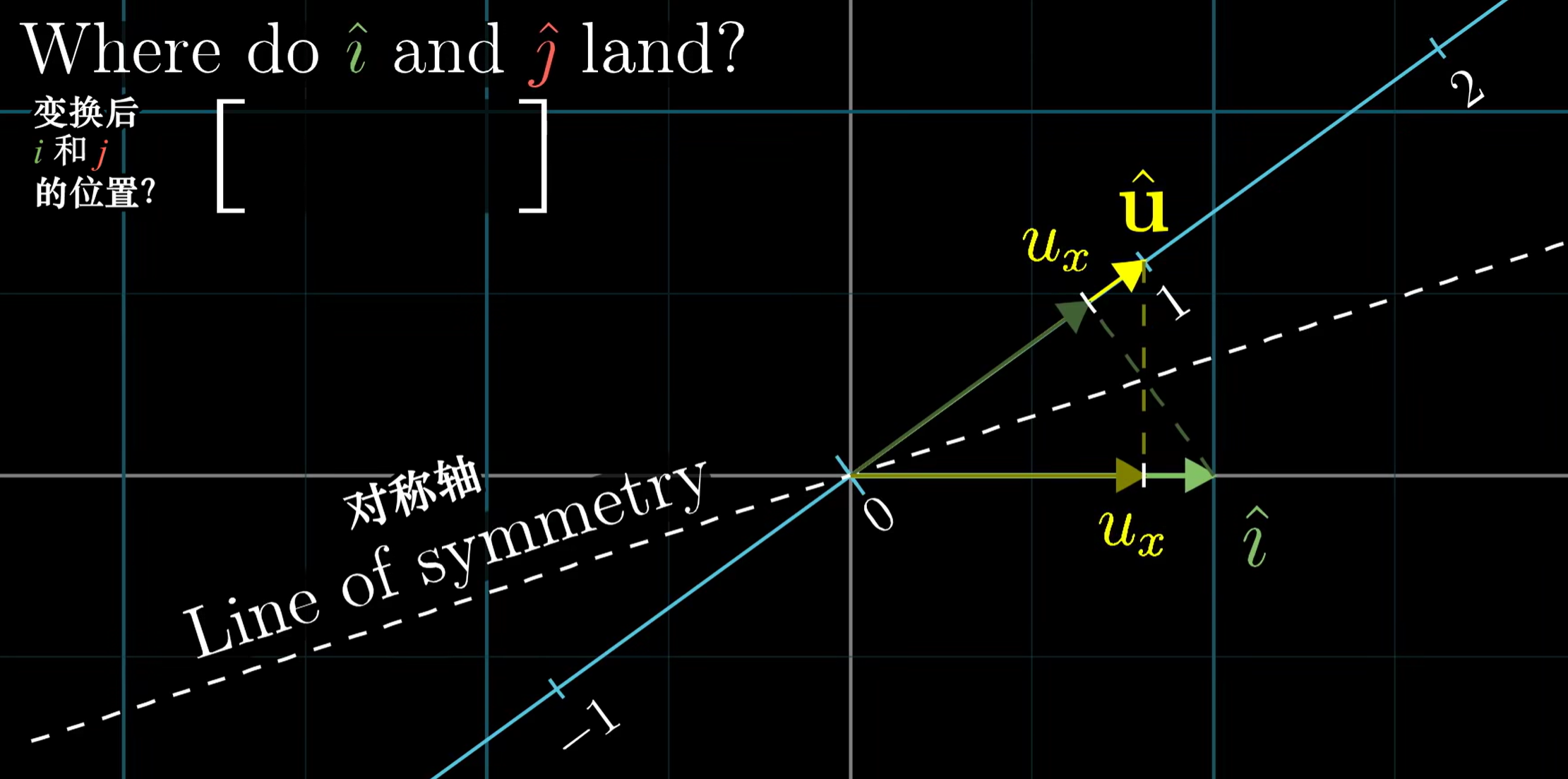
由于$i,j,u$的长度都是相同的(都是1),因此实质上具备对称性:
- $i$线性变换后的刻度值 = $u$投影到$i$的长度 = $u_x$
- $j$线性变换后的刻度值 = $u$投影到$j$的长度 = $u_y$
因此任意向量在指定单位向量上的投影值,可以表示为与这个单位向量的点积
对于非单位向量,似乎只是$u_x,u_y$乘上了一个长度系数
对于点积的结果,正是投影长度乘以这个长度系数
对偶向量
$$ f_v(w) = v \cdot w $$此时向量$f_v(w)$就是一个通过线性变换$v$,由$w$得到的一个一维向量
这一类向量$f_v$被称为对偶向量
即:构造了一个等价的线性函数,描述了一类操作
叉积
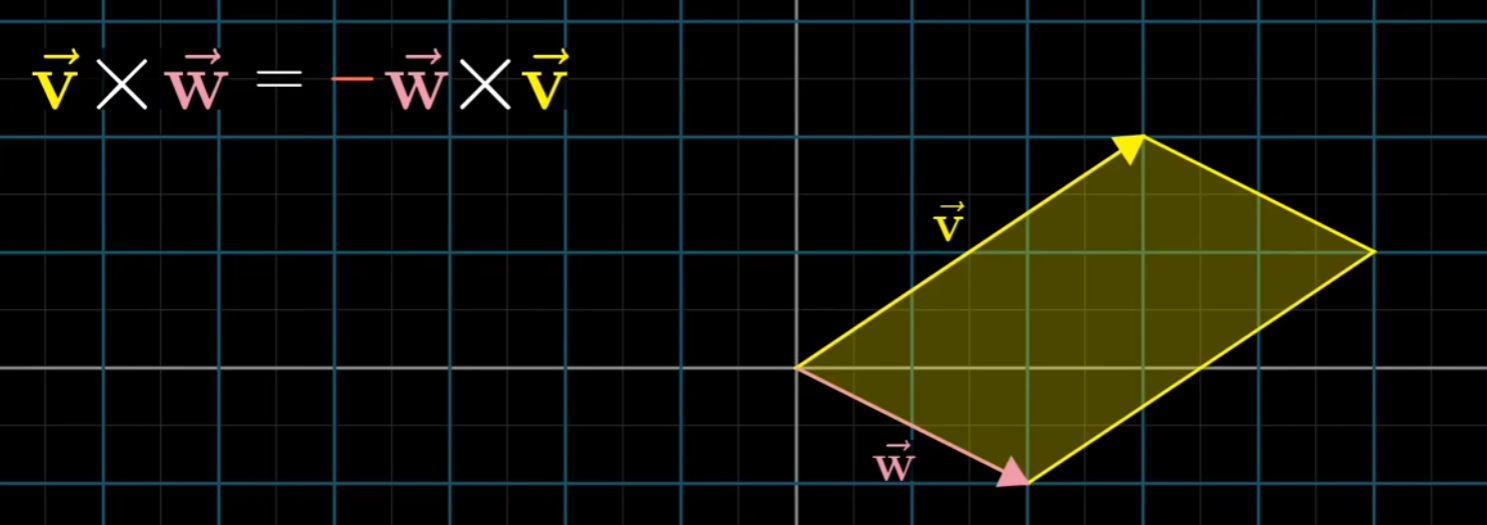
- 对于二维平面,在几何意义上,叉积代表了两向量之间的有向面积
- 并且这个值可以通过行列式(反应面积)衍生而来
更具意义的是,两个向量的叉积,实质上得到的是一个新向量
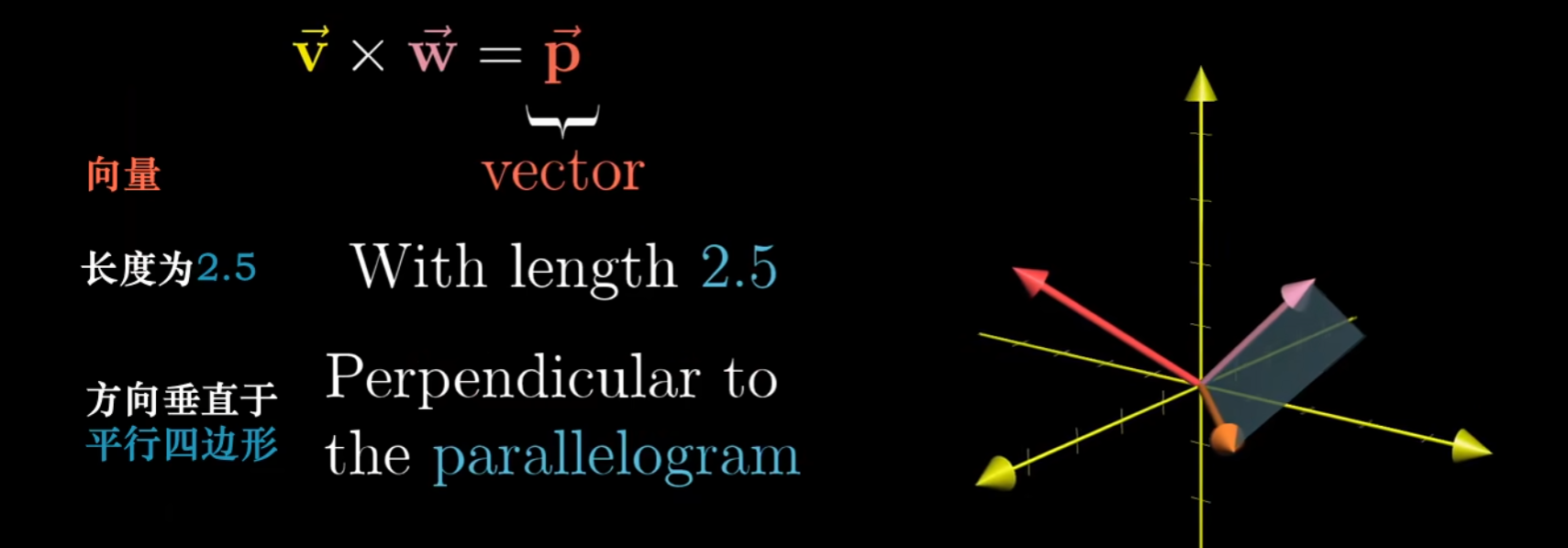
- 法向量的长度等于两个向量的有向面积
- 方向符合右手定则
这里我们仿造点积部分,我们希望定义一个线性变换,找到其对偶向量,并且说明对偶向量就是叉积的结果
对于两个三维的向量,其叉积的结果:
$$ \begin{bmatrix} x_1\y_1\z_1
\end{bmatrix} \times \begin{bmatrix} x_2\y_2\z_2
\end{bmatrix} = \det (\begin{bmatrix} i & x_1 & x_2\ j & y_1 & y_2\ k & z_1 & z_2
\end{bmatrix} ) $$
最后得到的$(i,j,k)$系数,即为对应的叉积向量
我们不如把$(i,j,k)$抽象成一个函数:
$$ f(\begin{bmatrix} x\y\z
\end{bmatrix}) = \det (\begin{bmatrix} x & x_1 & x_2\ y & y_1 & y_2\ z & z_1 & z_2
\end{bmatrix} ) $$
我们的目标是找到一个对偶向量$p$,使得:
$$ p\cdot \begin{bmatrix} x\y\z
\end{bmatrix} =\begin{bmatrix} p_1\p_2\p_3
\end{bmatrix}\cdot \begin{bmatrix} x\y\z
\end{bmatrix} = f(\begin{bmatrix} x\y\z
\end{bmatrix}) = \det (\begin{bmatrix} x & x_1 & x_2\ y & y_1 & y_2\ z & z_1 & z_2
\end{bmatrix} ) $$
则有:
$$ p_1x+p_2y+p_3z = x(y_1z_2-z_1y_2)+y(z_1x_2-x_1z_2)+z(z_1y_2-y_1z_2) $$因此:
$$ p = \begin{bmatrix} y_1z_2-z_1y_2\z_1x_2-x_1z_2\z_1y_2-y_1z_2
\end{bmatrix} $$
当我们构造出这个对偶向量时,回到点积的几何意义上
- 将向量$(x,y,z)^T$投影到$p$上,并且将长度与$|p|$相乘
再回到三维叉积的几何意义上:
- 三个向量所围成的平行六面体的有向体积
我们可以计算一下这个六面体的有向体积:
定义$v = (x_1,y_1,w_1)^T, w = (x_2,y_2,w_2)^T$
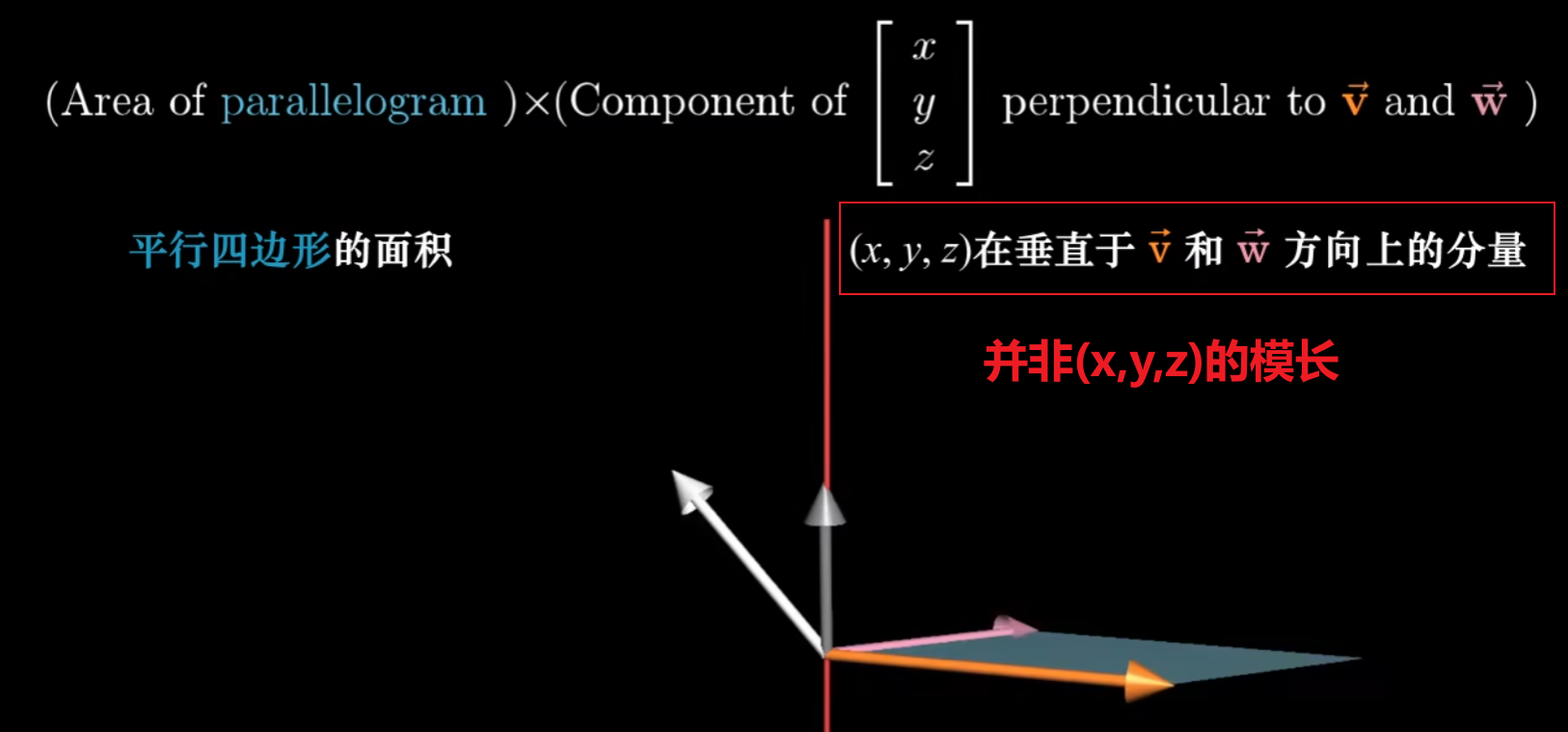
因此可以说明为:将$(x,y,z)^T$投影到$v,w$法向量上,并且与$v,w$的平行四边形的有向面积相乘
注意:法向量的长度,恰好等于$v,w$的平行四边形的有向面积
因此整个过程可以被概括为:$(x,y,z)^T$与$v,w$法向量的点积
基变换
选用不同的基向量,表达的方式自然会有些不同
- 选用$i,j$:网格方方正正
- 选用其他基向量:网格有一定倾斜

对于空间中的同一个向量,不同的基向量选择,自然会使用不同的线性组合进行表示
假设选取一组基向量:
$$ b_1 = \begin{bmatrix} 2\1
\end{bmatrix},b_2 = \begin{bmatrix} -1\1
\end{bmatrix} $$
对于向量$(-4,1)^T$,可以表示为以下两种方式:
- $(-4,-1)^T = -4i+j$
- $(-4,1)^T = -b_1 + 2b_2$
似乎可以通过矩阵表示:
$$ \begin{bmatrix} 2 & -1\1 & 1
\end{bmatrix}\begin{bmatrix} -1\2
\end{bmatrix} = \begin{bmatrix} -4 \1
\end{bmatrix} $$
概括这个线性变换:
$$ \begin{bmatrix} 2 & -1\1 & 1
\end{bmatrix}v = w $$
- $v$代表$b_1,b_2$空间下的向量表示
- $w$代表$i,j$空间下的向量表示
有趣的是,$b_1,b_2$的数值是基于$i,j$进行表示的
也就是使用了$b_1,b_2$视角下的$v$,左乘了$i,j$视角下的基向量矩阵,得到$v$在$i,j$视角下的$w$
假设我们使用一个线性变换:逆时针旋转90°
对于$i,j$作为基向量的空间,只需要追踪$i,j$变换后的位置,这个线性变换可以轻松表示为:
$$ M = \begin{bmatrix} 0 & -1\1 & 0
\end{bmatrix} $$
我们好奇在$b_1,b_2$视角下的旋转矩阵应该是怎么样的
对于需要旋转的向量$v$($b_1,b_2$视角),我们可以先把他转化到$i,j$下
$$ \begin{bmatrix} 2 & -1\1 & 1
\end{bmatrix}v $$
然后就可以自然代入旋转矩阵:
$$ \begin{bmatrix} 0 & -1\1 & 0
\end{bmatrix}\begin{bmatrix} 2 & -1\1 & 1
\end{bmatrix}v $$
最后我们需要转化回$b_1,b_2$视角,乘上一个逆矩阵即可:
$$ \begin{bmatrix} 2 & -1\1 & 1
\end{bmatrix}^{-1}\begin{bmatrix} 0 & -1\1 & 0
\end{bmatrix}\begin{bmatrix} 2 & -1\1 & 1
\end{bmatrix}v $$
令这个转化矩阵为$A$,则整个旋转矩阵可以归纳为:
$$ A^{-1}MA $$特征变换与特征值
对于一个线性变换$A$,总有一些向量在变换前后,仍然在同一条过原点的直线上
这些向量被称为特征向量$v$
同时由于存在一定比例的拉伸,这个比例被称为特征值$\lambda$
$$ Av = \lambda v $$由于右边是数乘,会比较麻烦,所以通常处理为:
$$ Av = (\lambda I)v \\ (A-\lambda I)v =0 $$也就是说一个向量$v$要被线性变换$A-\lambda I$压缩成零向量
能做到这一点的只能是$rank=0$的线性变换
这里通过行列式就能求解
抽象向量空间
接下来我们将超出2、3维,把线性抽象到函数层面
我们对于函数也能做线性变化
- $L(f,g) = L(f) + L(g)$
- $L(f) = cL(f)$
很巧,求导完美符合这两条性质
因此对于一个多项式,求导可以使用矩阵进行表示
