论文笔记 DLM

TiDAR - Think in Diffusion, Talk in Autoregression

看看其他工作

Large Language Diffusion Models

[TOC]

Intro

memory-bound

  • AR模型的Latency：每次predict next token，模型权重、KV Cache需要从显存中加载到GPU核心
    • 瓶颈是显存带宽，GPU计算密度远远不够
    • 因此单次decode越多的token，计算密度越高（在memory-bound的限制之下）

对于单次推理

  • AR：
$$ x_{t+1}=F(x_{< t};x_t) $$
  • dLMs：
$$ x_{t+1},x_{t+2},...,x_{t+k+1} = F(x_{< t};M_{t+1},M_{t+2},...,M_{t+k+1}) $$

只要没有触发到compute-bound

两者时间开销是一致的

意味着多预测的部分$x_{t+2},…,x_{t+k+1}$​是免费的，没有额外的时间开销

论文将这部分多预测出来的部分（在不增加开销的情况下），命名为Free Token Slots

什么是slots？

模型的输出是多个token，其中需要计算kv的部分认为是slots

剩余已经计算过kv的token，以下实验证明了影响不大

因此paper主要聚焦于slots

这里做了一个基于qwen3-32B的实验（Flash Attention 2、H100、batch size=1）

三条线分别是prefix=1024、2048、4096（kv cache提前计算好）

输入：token1 token2 ... token1023 token1024 [slots1] [slots2] ... [slotsn]

输出：logit1 loggit 2 ...

  • 因此实际影响单次forward的是输入的slots的数量

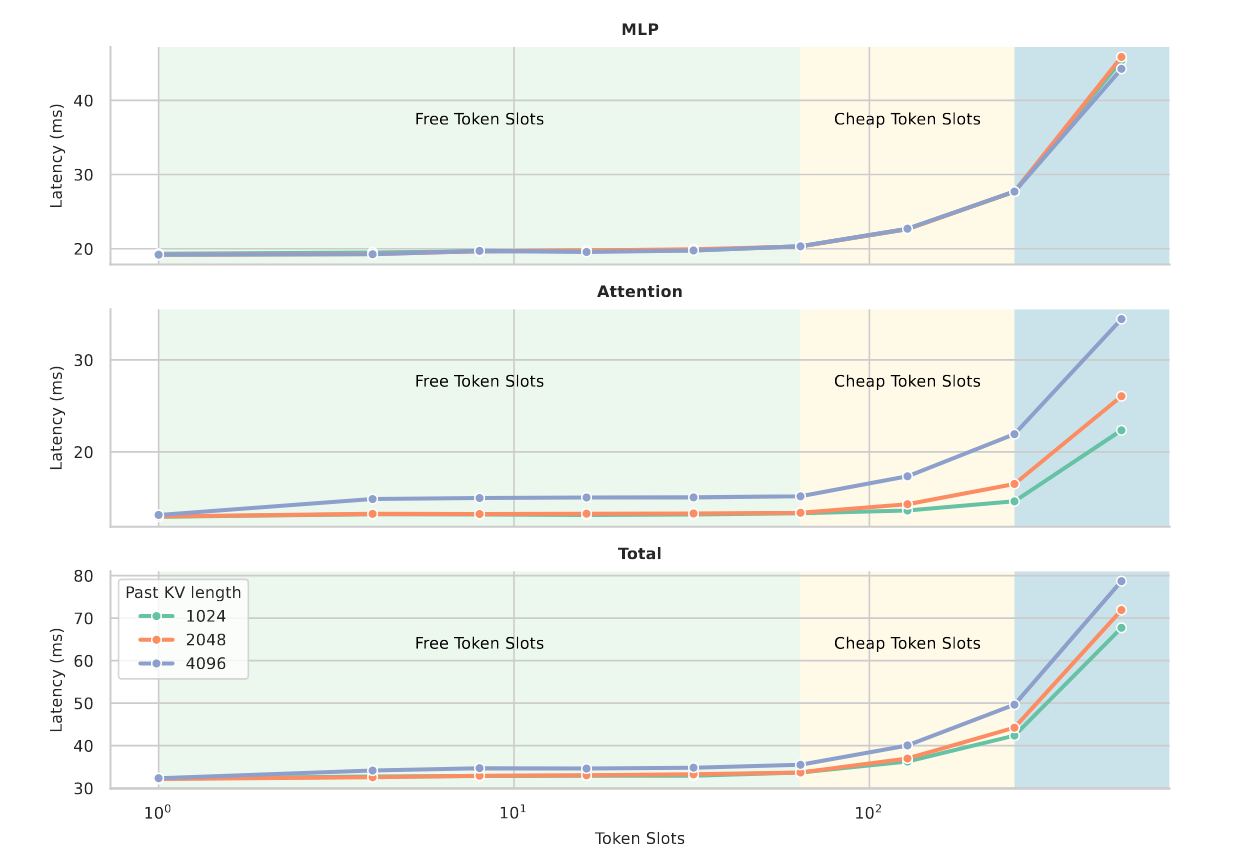
Free Token Slots

  • Free Token Slots：该区间（1 - 100）延迟基本不增加
  • Cheap Token Slots：该区间延迟增加的不多，比较cheap
  • 蓝色区间：触发了compute-bound

independence

  • AR是条件概率，按照从左到右依次生成
  • dLMs从加噪序列中decode所有的token
    • 我们通过策略选择采样$k$个token进行保留，其他进行remask

而被采样的token应该是多个边缘分布的乘积

$$ \prod_i p_\theta^i(x^i\mid x_t) $$

这些token都是基于解码前的加噪序列得到的条件概率生成

彼此可以看成独立的

这里不太认可。生成的时候并不是模型独立生成每一个token，而是同时生成

你要说完全独立没关系我觉得是不对的

  • 省流，从概率建模的角度解释dLMs的生成质量与$k$高度相关
    • $k=1$时，从左到右（因果掩码），退化成AR LLM
    • $k$越小，质量越高

real-intro

  • Challenge：生成模型的质量-并行问题

    • AR LLM：生成质量高，但是苦于memory-bound无法提升性能

    • dLMs：由于token间的独立性假设，生成质量受限于并发量

  • Contribution

    • 提出TiDAR架构，利用Free-token-slots，并行完成基于扩散的草稿和基于自回归的采样
    • 提供完整训练方案，进行全面评估，证明架构的优势
    • 进行详细的消融实验，验证核心设计。同时从扩散模型、投机采样角度进行分析

Method

修改一下论文顺序，先写一下怎么推理

  • 为了利用free-token-slots，需要Diffusion和AR同时在一次forward中同时出现

Fully Parallelizable Self-Speculative Generation

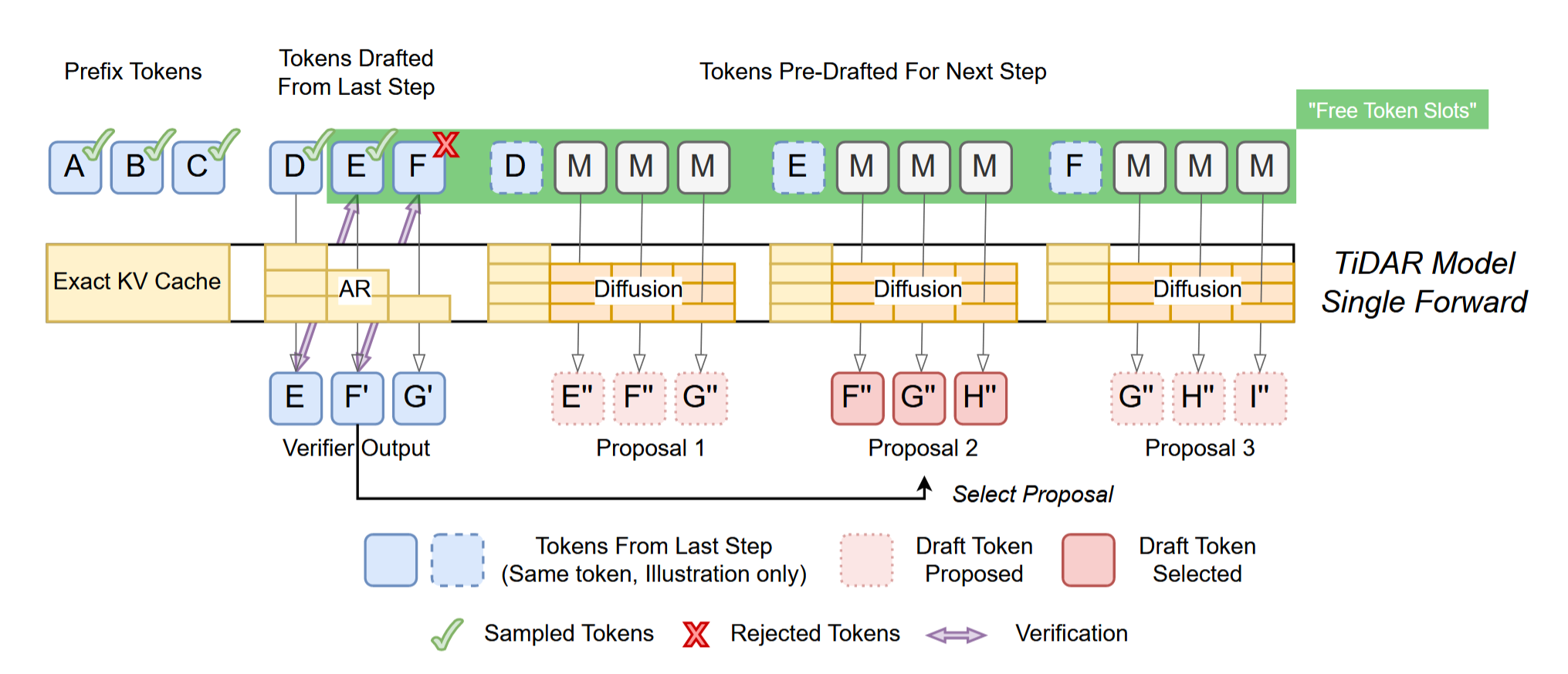
整个过程类似投机采样，整体的思想如下：

  • 首先由Diffusion Model生成一个draft
  • 由AR进行rejection sampling
    • 如果和AR的prediction一致，则保留
    • 否则直接丢弃

In the each subsequent decoding step, draft tokens from the last step are rejectively sampled by checking whether they match the prediction from the autoregressive joint distribution computed at current step using causal attention.

概述整个算法（定义block_len为3（可调整）），即我们会以三个token三个token为一组进行讨论

  • Step0：Draft初始化
    • 输入Prefix Tokens（实质上就是Prompt）和block size（这里是3）个MASK
    • 为了兼容不同长度，同样调整了Attention Mask的顺序
      • (block_size + max_seq_len,block_size + max_seq_len)
      • 直接按照真实长度切出来

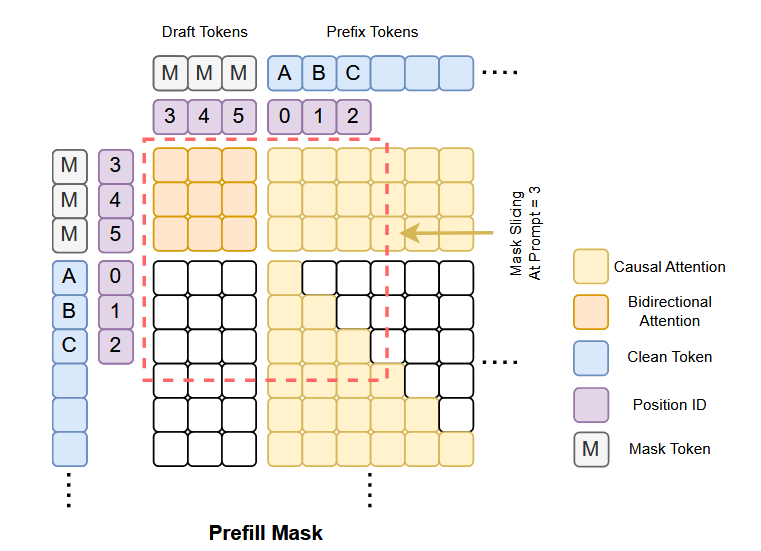
Prefill

  • Step1: 输入

    • Prefix Token：ABC，表示为之前已有（被成功采样）的token序列，提前计算好KV-Cache
    • Diffusion Draft：由Diffusion生成的草稿DEF

  • Step2: 并行处理两件事（实质上是一个Transformer模型的单次前向推理）

    • AR部分：基于Causal Attention，输出Diffusion Draft部分对应的logits（带有shift）

    • DLMs部分：假设所有拒绝采样的结果，提前准备好对应的[MASK]让DLM独立预测（生成下一轮使用的草稿）

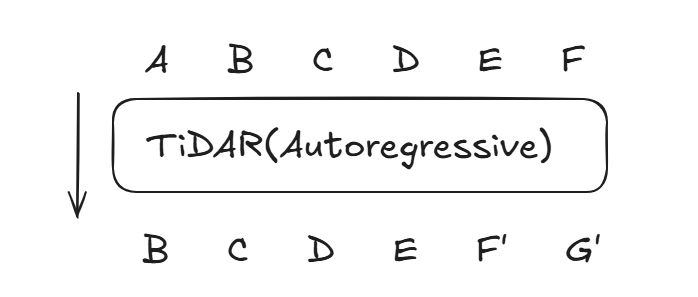
AR Shift

因此我们本质上把ABC DEF [M][M][M] [M][M][M] [M][M][M]作为输入

送入到TiDAR中，做了一次前向传播

这里调整了Prefix的顺序，方便复用Attention Mask矩阵，新采样的token直接加到最后

也就是DEF [M][M][M] [M][M][M] [M][M][M] ABC...

注意这里只是Attention Mask的顺序，并不是输入序列

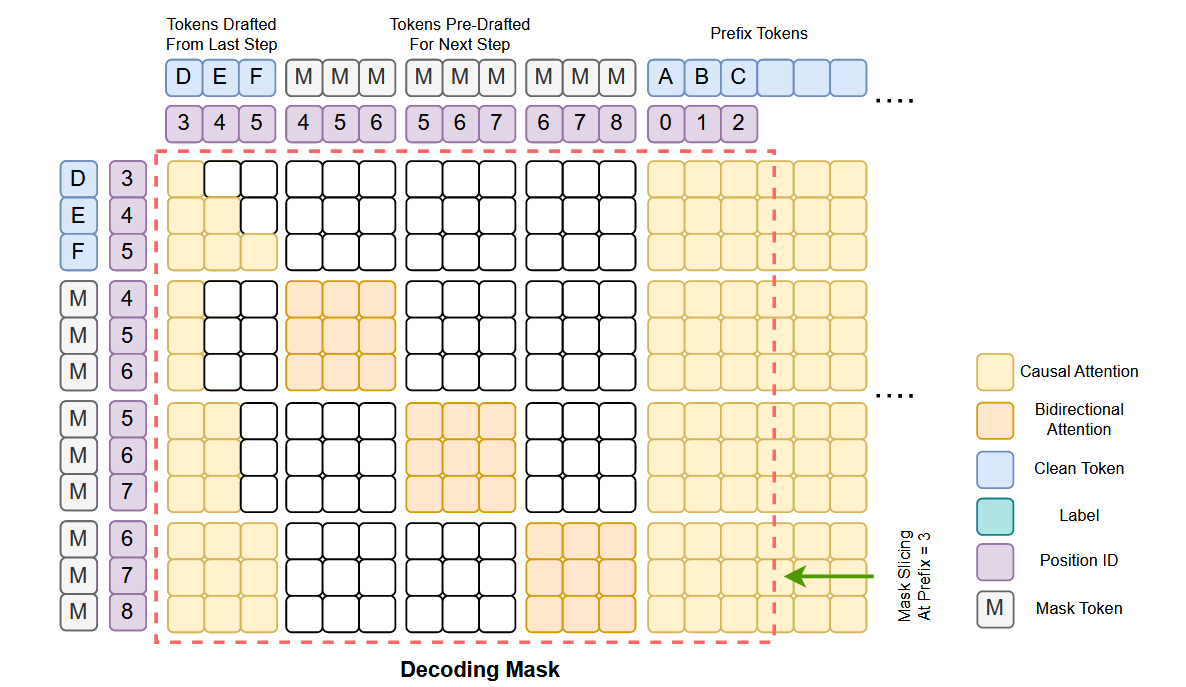
Decode

  • 对于第一组[M][M][M]：Attention能看见的是ABC D [M][M][M]
  • 对于第二组[M][M][M]：Attention能看见的是ABC DE [M][M][M]
  • 对于第三组[M][M][M]：Attention能看见的是ABC DEF [M][M][M]
  • Step3: Sampling
    • 根据AR部分的logits输出，决定上一轮草稿保留的内容（例子是保留DE，舍去F）
    • 因此Prefix Token和KV-Cache会将DE加入，得到ABC DE
    • 下一轮的草稿为第二组[M][M][M]的解码结果：F"G"H"
  • Step4：输出
    • Prefix Token：ABC DE及其KV-Cache
    • Diffusion Draft：由Diffusion生成的草稿F"G"H"

一些思考：

  • 显然block_len是不能无限大的，结合Figure1，通过单个Transformer架构的slots需要在Free-Token-Slots的范围内
  • paper只为AR采样1、2、3个token做了准备草稿，默认接受至少一个

Diffusion-AR Dual-mode Backbone Training

论文其实是先讲的这一部分，但是先看完推理后再回来看train比较好

前期工作Block Diffusion提出了一种块内双向注意力，块间因果掩码的方法

TiDAR进行了修改：保留最后一个块（双向注意力），其他内容（或者叫前缀）全部因果掩码

带来如下好处

  • 允许我们像AR一样计算链式的联合概率分布$p(x_i\mid x_{<i})$，方便进行拒绝采样，保证高质量，并且计算似然和AR一样高效
  • 在预训练和微调过程中可以计算前缀部分的NTP损失，损失信号的密度更高，充分利用数据中每一个token
  • AR部分：shifted by one position
  • dLM部分：一一对齐

TiDAR对于扩散部分的token，全部掩码为[MASK]，直接消除选择哪一种掩码策略的思考

  • 提高了扩散损失的密度（每一个token都参与）
  • 平衡了AR和扩散的损失：强制两者参与损失计算的token数量都是相等的（序列长度）
    • 先前框架的不平衡：dLM的信号容易被AR淹没
      • AR：稠密的（len-1个token参与）
      • dLMs：损失取决于多少token被掩码（远少于len）
    • 平衡的好处：更容易通过一个简单的超参数（加权因子）进行控制
    • 允许在推理时一步扩散，避免多步迭代

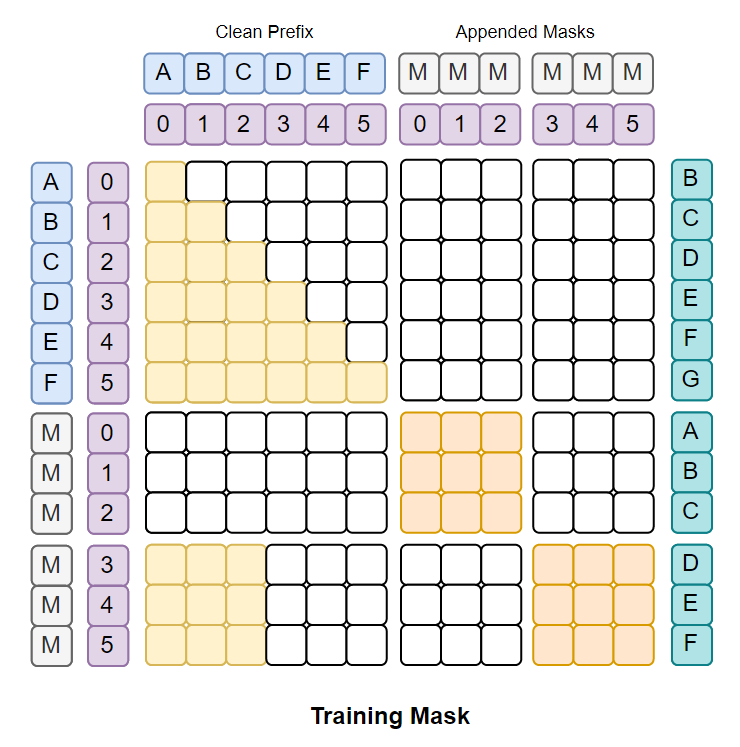
Train Mask

  • 对于输入序列，扩充相同的长度掩码ABC DEF -> MMM MMM
  • 前一半序列的注意力就是Causal Attention
  • 对于Diffusion部分（后一半），按照block size逐块考虑（采用双向注意力）
    • 第一组MMM恢复目标是ABC，前缀为空
    • 第二组MMM恢复目标是DEF，前缀为ABC
    • 若后续还有别的组，前缀会继续累积

TiDAR的建模目标可以表示为：

$$ \mathcal{L}_{TiDAR}(\theta) = \frac{1}{\alpha+1}\left( \sum_{i=1}^{S-1}\frac{\alpha}{S-1}\cdot\mathcal{L}_{AR}(x_i,x_{i+1};\theta)+ \sum_{i=1}^{S-1}\frac{1}{S-1}\cdot \mathcal{L}_{Diff}(\left[mask\right],x_i;\theta)\right ) $$
  • $\alpha \in[0,1]$，损失函数的平衡项（paper里设为1）
  • $\left{x_i\right}_S$是输入序列
  • AR和Diffusion都是做对应的交叉熵

Experiment

（这里笔记忘记保存了，补一些重点）

由于AR部分的logits是带label shift的，Diffusion部分没有

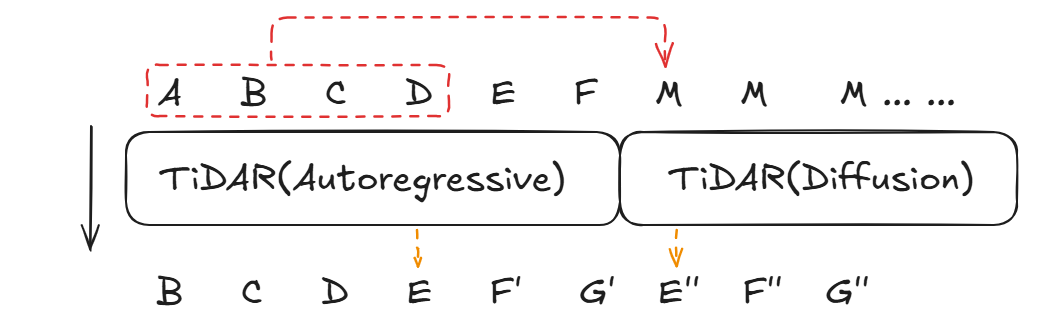
实质上是一个模型，没有切割

自回归部分根据ABCD会进行一个E的预测

Diffusion部分的第一个Mask，也会根据attention得到相同的信息，预测E''

所以这里涉及到了相信自回归还是相信Diffusion、或是兼顾的思考

作者顺手做了一个实验

$$ \text{logits}_{\text{mix}} = \beta*\text{logits}_i^{\text{AR}} + (1-\beta)*\text{logits}_i^{\text{Diff}},i\in|\text{Vocab}| $$

通过$\beta$对齐了两个logits

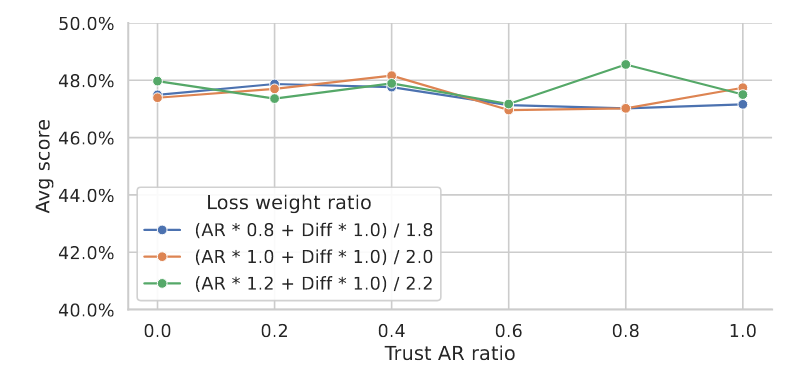
  • 通过$\alpha$控制loss比例，横轴是$\beta$
  • 总体没有明显性能差距，因此质量来源是拒绝采样，而非AR比DLM好

Limitations

  • Batch_Size：paper只做了1的情况（毕竟贴近推理，而不是吞吐量测试）
  • 长上下文：翻了一倍文本，压力比较大
  • free token slots的探索：需要更加系统化的视角
    • cuda
    • 调度
    • ……
DLM
Licensed under CC BY-NC-SA 4.0
© 2020 - 2025 Example Person
使用 Hugo 构建
主题 Stack 由 Jimmy 设计